Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 2: Gas Laws
Part e: The Ideal Gas Law
Part a: Pressure and Temperature
Part b: Volume and Temperature
Part c: Pressure and Volume
Part d: Volume and the Number of Moles
Part e: The Ideal Gas Law
Part f: Combined Gas Law
Part g: Dalton's Law of Partial Pressure
Part h: Graham's Law of Effusion
The Predictable Behavior of Gases
Pressure. Volume. Temperature. Number of moles. These are the four state variables that describe a sample of gas. It should be clear from the four previous pages of Lesson 2 that gas behavior is very predictable. The behavior of a gas, the manner in which these variables change as the result of a change in another variable, is described by precise equations. On this page of Lesson 2, we will learn the BIG equation - the ideal gas law equation. This equation epitomizes predictability. Knowing the value of three state variables, the ideal gas law equation allows us to predict the value of the fourth variable.
The Ideal Gas Law
Three of our four gas laws from Lesson 2 involve volume. They are
The k values in these equations are proportionality constants. We could conclude from these three equations that the volume of a gas is directly proportional to the temperature and the number of moles and inversely proportional to the pressure. We might right this as
P = R•n•T/V
where R is a proportionality constant. The equation above is known as the ideal gas law equation. We will write the equation as
P• V = n• R•T
and you can remember it easily by saying PIVNERT. The PIVNERT equation may be the most commonly used equation in the study of gases.
Because values of P, n, T, and V are measurable, the value of the proportionality constant can be determined. Its value will depend on the units of measurement for the four state variables. Here are values for several different units.
R = 0.08206 L•atm/mol/K
R = 62.36 L•torr/mol/K
R = 8.314 kPa•L/mol/K
The value of R is referred to as the ideal gas constant or the universal gas law constant.
The “Ideal” Idea
There is a reason that we call this equation the ideal gas law equation and not just the gas law equation. In Chemistry, we often refer to a gas sample as being an ideal gas if it follows the above law. If P•V/(n•R•T) is equal to 1, then the gas is ideal. But not every gas sample behaves as if it were ideal and the ideal gas law is not an effective predictor of its behavior. Those that clearly don’t are sometimes referred to as a real gas.
This doesn’t mean that an ideal gas is imaginary or a figment of one’s imagination. The ideal gas law is an approximation. The extent to which a gas sample matches this approximation is the extent to which it is ideal. Under certain conditions, we expect gases to match the approximation quite closely or even exactly. That is, P•V/(n•R•T) is equal to 1 for the gas sample. Those conditions usually involve moderate to low pressures and relatively high temperatures. But as temperatures decrease and/or pressures increase, one observes departures from the ideal situation and the gas is referred to as a real gas. A different equation is required to describe such gases. We will return to a discussion of ideal and real gases in Lesson 4. Until then, we will work with the assumption that the gas samples we’re discussing are good approximations of an ideal gas.
Derivation of Two-Variable Gas Laws
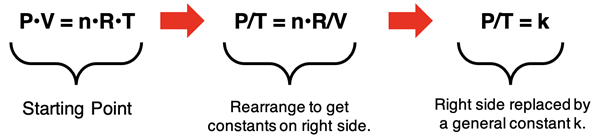
The ideal gas law is consistent with our previously discussed gas laws. We can use some good logic and algebra to derive the four gas laws from the ideal gas law. Each has some conditions that we will have to consider in the derivation. For instance, Gay-Lussac’s pressure-temperature gas law assumed conditions of constant volume (V) and number of moles (n). The derivation involves using algebra to isolate the constants (n, R, and V) on one side of the equation. The derivation is shown below, leading to the P/T = k expression of Gay Lussac’s Law.
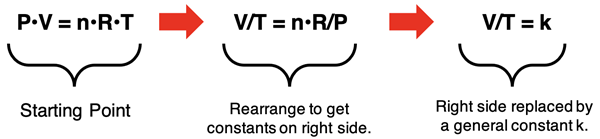
Charles’ Law can be derived for conditions of constant pressure and number of moles. The derivation involves using algebra to isolate the constants (n, R, and P) on one side of the equation. This is shown below, leading to the V/T = k expression of Charles’ Law.
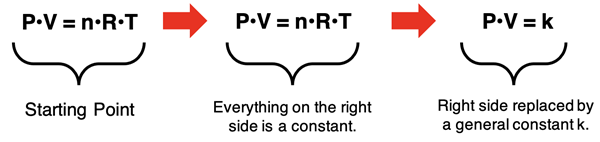
Boyle’s Law assumes constant temperature and number of moles. Algebra is used to isolate these constants (n, R, and T) by themselves on one side of the equation. This is shown below, leading to the P•V = k expression of Boyle’s Law.
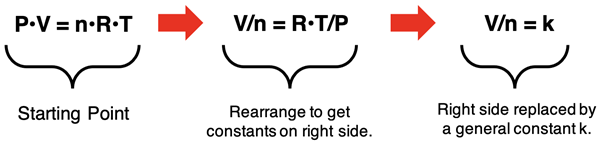
Finally, Avogadro’s Law assumes constant temperature and pressure. Algebra is used to isolate these constants (R, P, and T) by themselves on one side of the equation. This is shown below, leading to the V/n = k expression of Avogadro’s Law.
Solving PIVNERT Problems
The ideal gas law is often used to solve problems. Each problem typically provides information about three of the four state variables and asks for the determination of the value of the fourth variable. We will show three examples here with worked out solutions. Additional examples can be found in the Check Your Understanding section.
Example 1
The pressure and temperature of a 7.10 L sample of gas is 1.59 atm and 21.4°C. Calculate the moles of gas in the sample.
Solution:
We recommend that you begin by writing down the given values, equating them with the appropriate symbol. Then identify the unknown value. Finally, substitute the numerical values into the equation and solve using proper algebra. The solution looks like this:
Given:
V = 7.10 L
P = 1.59 atm
Temp = 21.4°C (add 273.15 for K) ==> T2 = 294.55 K
Unknown: n = ???
Equation: P•V = n•R•T where R = 0.08206 L•atm/mol/K
Rearrange equation to solve for n: n = P•V / (R•T)
Substitute values into the equation:
n = (1.59 atm) • (7.10 L) / [ (0.08206 L•atm/mol/K) • (294.55 K) ]
Use your calculator to solve: n = 0.467 mol (rounded from 0.4670516 …)
Note that the temperature values were converted to Kelvin temperature before substituting into the equation. Also be conscious of all units. Do some pre-converting of given quantities to the unit used for that quantity in the gas constant. For the R value used in this solution, V is in liter, P is in atm, and T (as always) is a Kelvin temperature. So, if V is given in units of mL, convert it to L before substituting into the ideal gas law equation.
Example 2
An 828-mL sample of helium gas contains 0.215 moles of gas at a temperature is 24.4°C. Calculate the pressure of the gas sample.
Solution:
Given:
V = 828 mL ==> V = 0.828 L
n = 0.215 mol
Temp = 24.4°C (add 273.15 for K) ==> T2 = 297.55 K
Unknown: P = ???
Equation: P•V = n•R•T where R = 0.08206 L•atm/mol/K
Rearrange equation to solve for P: P = n•R•T / V
Substitute values into the equation:
P = (0.215 mol) • (0.08206 L•atm/mol/K) • (297.55 K) / (0.828 L)
Use your calculator to solve: P = 6.34 atm (rounded from 6.3401508 …)
Note how both the given volume and temperature had to be pre-converted to the proper unit in order to match the units of V and T in the ideal gas law constant.
Example 3
There are 0.994 moles of nitrogen gas in a balloon that has a volume of 15.9 L at a pressure of 149 kPa. Determine its temperature in °C?
Solution:
Given:
V = 15.9 L
n = 0.994 mol
P = 149 kPa
Unknown: T = ???
Equation: P•V = n•R•T where R = 8.314 kPa•L/mol/K
Rearrange equation to solve for T: T = P•V / (n•R)
Substitute values into the equation:
T = (149 kPa) • (15.9 L) / [ (0.994 mol) • (8.314 kPa•L/mol/K) ]
Use your calculator to solve: T = 286.67313 … K
Now convert to °C:
Temp = 286.67313 … K - 273.15 K
Temp = 14 °C (rounded from 13.523129 …)
Note that an early decision was made as to whether to convert the pressure to atm and use the R value of 0.08206 L•atm/mol/K or to keep the pressure in kPa and use the R value of 8.314 kPa•L/mol/K. Either method would have worked. The point though is to always give attention to units. Use the value of R that matches the units that are given.
Molar Volume Revisited
The concept of molar volume was discussed on the previous page of Lesson 2. Like molar mass, the molar volume is the volume of one mole of a gas. It is the V/n ratio of a gas sample. The ideal gas law can be rearranged to solve for molar volume. The molar volume is equal to R•T/P. It is dependent upon the pressure and temperature of the sample of gas. Now we can see how to calculate its value. As we mentioned, the molar volume of a gas is usually expressed for Standard Temperature and Pressure conditions (STP). Those conditions are a temperature of 273.15 K and a pressure of 1.00 atm. By substitution into our molar volume equation, we find that …
Molar volume = R•T/P = (0.08206 L•atm/mol/K) • (273.15 K) / (1.00 atm)
Molar Volume = 22.4 L/mol at STP conditions
While this is the molar volume at STP conditions, there is nothing preventing the calculation of the value at any set of temperature-pressure conditions.
Example 4
Determine the molar volume for the following pressure-temperature conditions:
- T = 298 K, P = 1.05 atm
- T = 373.15 K, P = 1.00 atm
- T = 225 K, P = 0.500 atm
Solution:
Use the R•T/P ratio to calculate the V/n ratio.
- V/n =R•T/P = (0.08206 L•atm/mol/K) • (298 K) / (1.05 atm) = 23.3 L/mol
- V/n =R•T/P = (0.08206 L•atm/mol/K) • (373.15 K) / (1.00 atm) = 30.6 L/mol
- V/n =R•T/P = (0.08206 L•atm/mol/K) • (225 K) / (0.500 atm) = 36.9 L/mol
Density and Molar Mass of a Gas
The ideal gas law allows us to relate the density of a gas to the molar mass of the gas. Density was defined in Chapter 2 of our Tutorial as being a measure of how concentrated mass is within a given volume of space. Mathematically, density is the mass per volume ratio. We will represent density by the Greek symbol ρ. If ρ = m/V, then the V = m/ρ. (That’s a couple of steps algebra that landed us on the V = m/ρ equation.) We can substitute the V = m/ρ ratio into the ideal gas equation for V and generate a density equation. The multiple steps of algebra are shown below:
The density equation is shown in the final line.
Example 5
Calculate the density of …
- Hydrogen gas (H2) at STP conditions.
- Carbon dioxide gas at STP conditions.
- Methane gas (CH4) at P = 1.00 atm and T = 625 K
Solution:
In order to do the above calculations, the molar masses will be needed. These can be acquired using atomic mass values from a periodic table. Values are:
H2: 2.016 g/mol
CO2: 44.01 g/mol
CH4: 16.04 g/mol
Now the equation can be used to calculate the density values:
a. H2 at STP conditions:
ρ = P•MM/(R•T) = (1.00 atm)•(2.016 g/mol)/[ (0.08206 L•atm/mol/K)•(273.15 K) ]
ρ = 0.08994 g/L
b. CO2 at STP conditions:
ρ = P•MM/(R•T) = (1.00 atm)•(44.01 g/mol)/[ (0.08206 L•atm/mol/K)•(273.15 K) ]
ρ =1.963 g/L
c. CH4 at P = 1.00 atm and T = 625 K:
ρ = P•MM/(R•T) = (1.00 atm)•(16.04 g/mol)/[ (0.08206 L•atm/mol/K)•(625 K) ]
ρ = 0.313 g/L
Before You Leave
- Download our Study Card on The Ideal Gas Law. Save it to a safe location and use it as a review tool. (Coming Soon.)
- Our Calculator Pad section contains five problem sets that would be fitting follow-up to this lesson. See Problem Sets GL7 - GL11 in the Gas Laws section. A problem set contains 5-6 problems with an answer box. Your answers are checked and you have endless opportunities to make corrections.
- The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1. How do real and ideal gases differ from one another?
2. Under what pressure and temperature conditions is a gas sample most likely to behave as an ideal gas?
3. Why is there more than one value of R? And which value should I use when solving PIVNERT problems?
4. Starting with the ideal gas equation PV = n•R•T, use algebra to write it in four different algebraic forms. Generate a P =, a V =, a n =, and a T= equation.
5. A container of nitrogen gas (N2) held at a temperature of 24.1°C and a pressure of 1.008 atm has a volume of 6.05 L.
a. Determine the moles of nitrogen gas in the container.
b. Determine the mass of the nitrogen gas.
6. An 8.95-L sample of gas has a temperature and pressure of 25.0°C and 2.85 atm. Calculate the moles of gas in the sample.
7. Does the molar volume of a gas depend on the identity of the gas? That is, would hydrogen gas and nitrogen gas have a different molar volume when present at the same temperature and pressure?
8. Does the density of a gas depend on the identity of the gas? That is, would hydrogen gas and nitrogen gas have a different density when present at the same temperature and pressure?
9. Calculate the volume of …
- 2 mol of SO2 gas at STP.
- 10 mol of NO2 gas at STP.
- 3.25 mol of N2 gas at STP.
10. Determine the density of a sample of Ar gas at 21.9°C and 726 torr.