Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 4: Density
Part a: Concepts and Mathematics of Density
Part 4a: Concepts and Mathematics of Density
Part 4b: Measuring Density
Matter Revisited
Earlier in this chapter, we defined matter as anything that has mass and volume. To be classified as matter, there’s two requirements:
- Mass: there has to be some stuff in the object.
- Volume: the stuff has to occupy some space.
Mass and volume. Stuff and space.
Density Concept

Density is a physical property of a material. It is closely tied to mass and volume. Mass is the amount of stuff in an object. And volume is the amount space the object occupies. Density has to do with stuff and space. The concept of density provides a measure for how concentrated mass is in a given amount of space. A relatively dense object has a relatively large amount of stuff in its space. A less dense object has a relatively small amount of stuff in its space. If you prefer the more technical language, simply exchange the word mass for stuff and volume for space.
Density is the ratio of the mass to the volume. Let’s conduct three thought experiments in order to make meaning of this concept.
Thought Experiment #1:
Consider three containers – A, B, and C - that have the
same volume. Each container contains the
same gas. But the number of gas particles in the containers vary. This situation is pictured below. How do the densities of the three samples compare?
Density is the ratio of mass to volume. Since each sample has the same volume, it is the sample with the greatest mass that will be most dense. The sample with the smallest mass will be least dense. The mass will depend on the number of particles of gas in the container. Thus, sample A will have the greatest mass and the greatest density. Sample C has the least number of particles and the smallest mass and smallest density.
Density of A > Density of B > Density of C
Thought Experiment #2:
Consider three containers – A, B, and C. Each container contains the
same gas. And each container has the
same number of particles. But the volume of the containers vary. This situation is pictured below. How do the densities of the three samples compare?
Density is the ratio of mass to volume. The mass of each sample will be the same since each sample contains the same number of particles of the same gas.
Since each sample has the same mass, it is the sample with the smallest volume that will be most dense. The sample with the greatest volume will be least dense. Thus, sample C will have the smallest volume and the greatest density. Sample C has the greatest volume and smallest density. Conceptually, you could say that the gas particles are more densely packed together in Sample C and less densely packed together in Sample A.
Density of C > Density of B > Density of A
Thought Experiment #3:
Consider three containers – A, B, and C - that have the
same volume. Each container contains a
different gas. The number of particles of each gas is the same for all three containers. This situation is pictured below. The
Atom Key provides information about the relative mass of the three types of particles. How do the densities of the three samples compare?
Density is the ratio of mass to volume. Since each sample has the same volume, it is the sample with the greatest mass that will be most dense. The sample with the smallest mass will be least dense. The mass will depend on the particle mass. Sample C contains the most massive particles. So, Sample C has the greatest mass and the greatest density. Sample A has the least massive particles, the smallest mass, and the smallest density.
Density of C > Density of B > Density of A
Density Equation
The equation for density is:
Equations are commonly written in symbol form. If we use the symbol
D to represent density, the symbol
m to represent mass, and the symbol
V to represent volume, then the equation becomes:
The units on density are mass units divided by volume units. The most common density unit for a Chemistry class is g/mL or g/cm
3. Other commonly used units are kg/L and kg/m
3. All these examples are consistent with the expression mass/volume.
Density is an identifying physical property. Because different substances have different densities, a measurement of the density of an unknown substance allows a chemist to identify the substance with a relative high degree of certainty. Density values for a variety of materials are shown in the table below.
Density, Floating, and Sinking

Liquids do not always dissolve in each other. Such liquids are said to be
immiscible. If you pour two such liquids into a container, they will separate out instead of mixing homogenously. Two layers are formed. Which layer is most dense? The general rule is that the more dense material will sink in the less dense material. Put another way, the more dense material buoys up the less dense material. And put still another way …
Less dense materials float on top of more dense materials.
A common classroom demonstration involves the creation of a
density column. An
example is shown at the right. Several immiscible liquids are added to the same graduated cylinder. Layers are formed with the more dense liquids being lower in the column.
The devastating impact that an oil spill has upon aquatic life is explained by this principle that less dense materials float on top of more dense materials. You’ve likely heard that oil and water do not mix. Crude oil is a mixture of several substances, nearly all of which are less dense than water and therefore float on top of water. Aquatic life – otters, seals, whales, dolphins, and birds – that must break the water-air interface on a daily basis to fish, hunt, or to obtain air are drastically affected by the crude oil that layers the water’s surface. The feathers of birds repel water, allowing them to quickly dry off and fly. But the fact that bird feathers repel water means that they readily absorb oils. Exposure to oil spills coats their feathers, rendering many of them essentially flightless.


With roughly 70% of earth’s surface covered by water, it is one of the more abundant substances on earth’s surface. It has many unique properties, one of which is that the solid form of water is more dense than the liquid form. This property is only shared by a few other substances. Unlike most substances, when water freezes, the solid form will float on top of the liquid form. The result is that bodies of water will never freeze from the bottom up to the surface. Instead, they freeze from the surface downward. As the layer of ice on top of water’s surface begins to expand, it provides thermal insulation for species that inhabit the water below its surface. Underwater life thus survives the harshest of winters. For our friends in underwater schools, that’s
Chemistry for Better Living.
Using the Density Equation
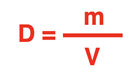
The density equation has three variables in it –
D,
m, and
V. If the value of any two of these three variables is known, the value of the third variable can be determined. The formula is set up so as to solve for density from knowledge of the value of mass and volume. But what if one wishes to solve for mass or volume? For those who are believers in algebra, that’s not a problem at all. The equation can be manipulated to obtain formulae for calculating mass or volume. The derivation below shows how to algebraically manipulate
D = m/V to obtain an
m = … equation.
The final need is to acquire a
V = … equation. The derivation below shows how to algebraically manipulate
D = m/V to obtain an
V = … equation.
We have now used the density equation to generate formulae for solving for density, mass, and volume.
Now it's time to use the formulae to solve for an unknown quantity.
Practice Problems
For the following problems, use the formulas to solve for the unknown. Then tap the button to view the answers.
Problem 1:
Graham Uvmass and Millie Leeders are doing the Density Lab. They determine that a block of wood has a volume of 76.3 cm
3. They determine that it has a mass of 67.7 g. What is the density of the block of wood?
Problem 2:
The element mercury has a density of 13.6 g/mL. Mrs. Mandochino finds a bottle in the chemical storeroom containing 563 mL of mercury. What is the mass of this liquid mercury?
Problem 3:
During the Properties of Elements lab, Jalen becomes enamored by the small block of sulfur on the lab table. He smells it, spins it, and even masses it, determining it to have a mass of 91.84 g. And then as the grand finale, he pulls out his calculator with enthusiasm to use the density of sulfur (2.07 g/cm
3) to calculate the volume of the lump. What value does Jalen calculate for the volume? (HINT: he never misses a Chemistry question.)
Problem 4:
(Challenge Problem)
Due to its malleability, gold can be hammered into extremely thin sheets known as gold leaves. Silvanna worked at the W&B Gold Leaf manufacturing facility last summer. Her typical routine involved measuring out a 710.0-mg nugget of gold and positioning it under the mechanical hammer. The hammer would then pound the gold into a 1.40 ft x 1.40 ft square shape with a relatively uniform thickness. The thickness of the final product is very, very thin. Gold has a density of 19.32 g/cm
3. What is the average thickness (in centimeters and in micrometers) of the gold leaf? (
Given: 1.00 inch = 2.54 cm)
You will find more practice problems of varying difficulty in the
Check Your Understanding section at the bottom of the page. And use the link in our
Before Your Leave section for even more interactive problems at our
Calculator Pad.
Other Types of Density

As mentioned above, the density concept provides a measure for how concentrated mass is in a given amount of space. We have been discussing
volumetric mass density – the mass/volume ratio. Volumetric density presumes 3-dimensional space.
As you continue in your studies of science, you will encounter other types of density definitions. For instance, the concentration of mass within a wire or cable is sometimes measured as the mass per length. It is given the name
linear mass density. Since wires or cables stretch out through space in one dimension, it makes more sense to measure the
concentration of mass as mass/length. If we need a measure of how concentrated mass is across a given area in two dimensions –
area mass density – we would define density as mass per area. This might be an important measure of mass concentration in the textile industry where the quality of a fabric is dependent upon the concentration of mass across the area of the fabric. Since fabrics are stretched out in space across two dimensions, it makes more sense to measure the
concentration of mass as mass/area.
The concept of density extends beyond mass. Manufacturers of car batteries

may be concerned about
energy density - the concentration of energy about the volume of the battery. A physicist may be concerned about
charge density – the concentration of charge in a conducting wire or on a conducting surface. Ecologists will study
population density - how concentrated a particular species is about a given area of a habitat. Regardless of what type of density we are referring to, it gives a measure of how concentrated some item or quantity is about a given region of space.

Before You Leave
Check Your Understanding
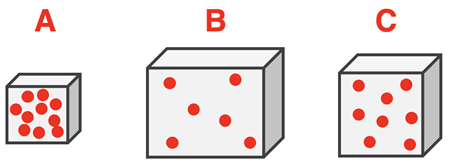
1. Consider three samples – A, B, and C - of the same gas present in containers that have a different volume. The particle diagrams show the relative number of gas particles in the three containers. Rank the three samples according to their density from smallest to greatest.
2. The measured mass and volume of three metal samples are shown. Rank the samples according to their density.

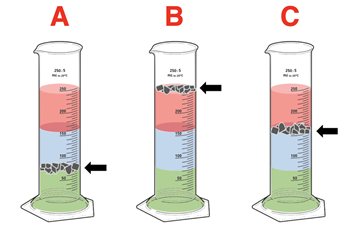
3. A density column is prepared in a cylinder using three different liquids, each colored with a drop of food coloring. Three samples of household objects – A, B, and C - are shredded and dropped into the cylinder. The diagrams show where the shredded materials settle. Rank the samples according to their density.
4. A pure sample of a material is measured to have a cuboid shape with side lengths of 1.65 cm, 1.10 cm, and 4.35 cm. It is determined to have a mass of 53.69 g. Determine the density of the material.
5. Jules Snatcher walks out of a store with 7.36-carat diamond inside his coat pocket. The density of diamond is 3.51 g/cm
3. Given that 1.00 carat = 0.200 grams, determine …
- ... the mass of the diamond in grams.
- ... the volume of the diamond in cm3.