Lesson 4: Kinetic Molecular Theory

Part a: Characteristics of the Model

Laws versus Models

Lesson 2 of Chapter 10 included a discussion of gas laws. Like any law in science, the gas laws describe the manner in which nature behaves. Specifically, the gas laws describe how a change in one state variable affects another state variable for a specific set of conditions. The word we would like to emphasize is describe. Laws describe a set of empirical observations.
 
A model or theory is not a law. While laws attempt to describe how nature behaves, a model attempts to explain why nature behaves the way that it does. A model provides a simplified representation or approximation of some aspect of nature. A model often begins with some assumptions about how a system is structured, how its parts relate to each other, and what mechanisms occur within the system that affect what is observed of the system. The model attempts to provide an explanation of the observed behaviors and/or mathematics of the system. The word we are emphasizing is the word explain.
 
Lesson 4 of Chapter 10 will present a model to explain why gases behave as they are observed to behave. The model is referred to as the Kinetic Molecular Theory. Like many models in Chemistry, the Kinetic Molecular Theory is a particle model. Macroscopic behavior is explained by fundamental rules regarding how a system of gas particles respond when properties of a gas are changed. This has been an ongoing theme throughout our Chemistry Tutorial: particle behavior affects and explains macroscopic observations.
 
Saying that the volume of a gas and the pressure of a gas are inversely proportional (Boyle’s Law) is an act of stating a law that describes macroscopic observables. Pressure and volume are quantities that are measured. They are observables, occurring at the macroscopic level. On the other hand, particles cannot be seen. By particles, we are referring to atoms and molecules. The atoms of helium in a sample of helium gas and the molecules of nitrogen in a sample of nitrogen gas cannot be seen, measured, or observed. Only the effects of their behavior can be observed. A model attempts to relate such particle behavior to the observable.
 

Assumptions of the Kinetic Molecular Theory

Like many models, the Kinetic Molecular Theory includes a collection of assumptions about the manner in which particles of a gas behave. Five of the common assumptions or postulates of the theory are described below.
 

Assumption 1: Motion of Gas Particles

Particles of a gas are in constant random motion about the container. They collide with each other and with the walls of the container. The collision with the walls contributes to the pressure of the gas.
 

Assumption 2: Size of Gas Particles

On average, particles in the gas state are very distant from one another. We say “on average” because they are in constant motion. While two particles may be widely spaced from one another at one instant in time, they could be moving towards each other and at a later instant be close enough to collide with each other. But in general, the distance between gas particles is very large compared to the interparticle distance in condensed states such as solids and liquids. And relative to the size of an actual particle, the average distance between particles is enormous. So much so that we can assume the space occupied by an actual particle is negligible compared to the volume of the container. Particles are essentially points in space.
 

Assumption 3: Forces between Gas Particles

The interparticle forces in a sample of gas are negligible or non-existent. Gas particles do not attract or repel other gas particles. Similarly, there are no attractive or repulsive forces between a gas particle and the walls of its container.
 

Assumption 4: Collisions of Gas Particles

Gas particles will collide with each other and with the walls of the container. Every collision is considered elastic. This is a Physics term that indicates that all the energy of motion is conserved by the system of two colliding particles during a collision. Energy of motion is known as kinetic energy. When two gas particles collide, one particle may slow down and the other particle may speed up but the total amount of kinetic energy remains unchanged. The kinetic energy that one particle loses equals the kinetic energy that the other particle gains. The total kinetic energy is conserved.
 

Assumption 5: Kinetic Energy of Gas Particles

Because of particle collisions, there is a range of speeds with which particles of the system move. As such, there is a range of kinetic energies. It is common to refer to the average speed (or root mean speed) and the average kinetic energy of the gas particles. The average kinetic energy of the particles of gas is directly proportional to the Kelvin temperature of the gas. This means if the Kelvin temperature is doubled, then the average of the kinetic energy of all gas particles in the system is also doubled. This also means that the average KE of the gas particles is 0 when the Kelvin temperature is 0 K.
 

Gas Pressure and the Container Walls

In general terms, pressure is the result of a force upon a given area. It is defined mathematically as the force divided by the area over which the force acts. Both quantities are important. A medium force over a large area may result in a small pressure that is hardly noticeable. But the same force over a large area is hard not to notice. A 150-pound person standing on the ground is hardly aware of the pressure that results from 150 pounds of force upon the area of their shoes. But if a 150-pound person stands on a sharp tack, the same 150-pound force is spread over a very small area, resulting in an enormous pressure; and you can bet that the person going to notice it.

 
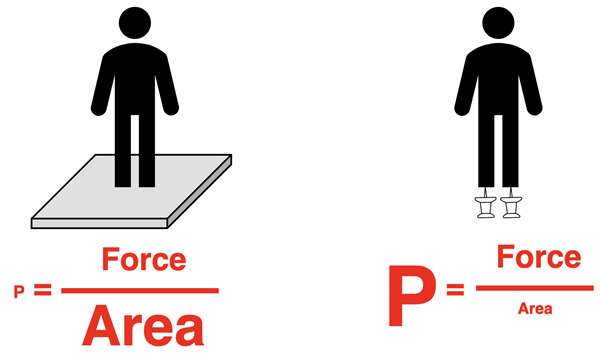
For a gas in a container, the pressure is the result of the cumulative force applied by all the particles of the gas as they collide with the container wall. The area is the area of the container that holds the sample of gas. We can reason that the pressure of a gas will depend upon the number of particles gas, the temperature of the gas, and the volume of the container. If a greater number of particles are present, then there will be collisions occurring every second and thus a larger force. If the temperature of the sample is higher, then the particles will be moving with more kinetic energy and applying a greater force with every collision. They will also be colliding more frequently since they cover the distance from one container wall to the opposite wall in less time. And a higher volume container is more likely to have a higher surface area, thus reducing the pressure that results from the collisions.
 
 
On the next page of Lesson 4, we will use our understanding of Kinetic Molecular Theory to explain the gas laws from Lesson 2.
 
 
 

Before You Leave

• Download our Study Card on Kinetic Molecular Theory. Save it to a safe location and use it as a review tool. (Coming Soon.)
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 

Questions coming soon.