Linear and Angular Velocity - Questions
The Linear and Angular Velocity Concept Builder is comprised of 52 questions. The questions are divided into 14 different question groups. Questions in the same group are rather similar to one another. The Concept Builder is coded to select at random a question from each group until a student is successful with that group of questions.
The questions and question groups are organized into three different activities. The activities are differentiated as follows:
- Turntable Physics: Question Groups 1-4: Students identify the situation with the greatest angular or linear velocity when given information about the rotating object.
- Case Studies: Question Groups 5-10: Students are given information about two rotational cases and determine how many times smaller or greater the angular velocity (or linear velocity) of Case A is than Case B.
- Do the Math: Question Groups 11-14: Students are provided quantitative information about a rotating object and must identify the proper expression for the angular velocity or linear velocity.
The questions from each group are shown below. Teachers are encouraged to view the questions in order to judge which level of difficulty is most appropriate for their classes. We recommend doing all three activities.
The Physics Classroom grants teachers and other users the right to print these questions for private use. Users are also granted the right to copy the text and modify it for their own use. However, this document should not be uploaded to other servers for distribution to and/or display by others. The Physics Classroom website should remain the only website or server from which the document is distributed or displayed. We also provide a PDF that teachers can use under the same conditions. We have included a link to the PDF near the bottom of this page.
Activity 1: Turntable Physics
Question Group 1
Questions 1
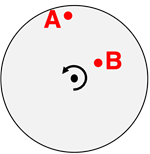
Consider the two objects – A and B – on the rotating turntable. Which object has the greatest angular velocity?
Object A has the greatest angular velocity.
Object B has the greatest angular velocity.
Both objects have the same angular velocity.
Questions 2
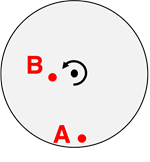
Consider the two objects – A and B – on the rotating turntable. Which object has the greatest angular velocity?
Object A has the greatest angular velocity.
Object B has the greatest angular velocity.
Both objects have the same angular velocity.
Questions 3
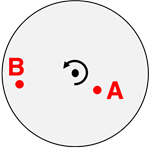
Consider the two objects – A and B – on the rotating turntable. Which object has the greatest angular velocity?
Object A has the greatest angular velocity.
Object B has the greatest angular velocity.
Both objects have the same angular velocity.
Questions 4
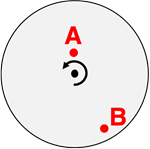
Consider the two objects – A and B – on the rotating turntable. Which object has the greatest angular velocity?
Object A has the greatest angular velocity.
Object B has the greatest angular velocity.
Both objects have the same angular velocity.
Question Group 2
Questions 5

Consider the two objects – A and B – on the rotating turntable. Which object has the greatest linear velocity?
Object A has the greatest linear velocity.
Object B has the greatest linear velocity.
Both objects have the same linear velocity.
Questions 6

Consider the two objects – A and B – on the rotating turntable. Which object has the greatest linear velocity?
Object A has the greatest linear velocity.
Object B has the greatest linear velocity.
Both objects have the same linear velocity.
Questions 7

Consider the two objects – A and B – on the rotating turntable. Which object has the greatest linear velocity?
Object A has the greatest linear velocity.
Object B has the greatest linear velocity.
Both objects have the same linear velocity.
Questions 8

Consider the two objects – A and B – on the rotating turntable. Which object has the greatest linear velocity?
Object A has the greatest linear velocity.
Object B has the greatest linear velocity.
Both objects have the same linear velocity.
Question Group 3
Questions 9
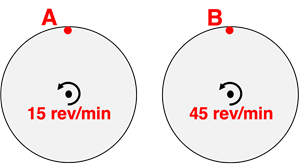
Two objects – A and B – are located on the outer edge of two different rotating turntables, each having the same radius but a different turning rate. Which object has the greatest linear velocity?
Object A has the greatest linear velocity.
Object B has the greatest linear velocity.
Both objects have the same linear velocity.
Questions 10
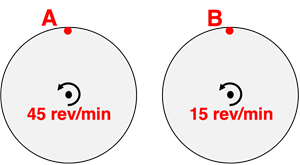
Two objects – A and B – are located on the outer edge of two different rotating turntables, each having the same radius but a different turning rate. Which object has the greatest linear velocity?
Object A has the greatest linear velocity.
Object B has the greatest linear velocity.
Both objects have the same linear velocity.
Questions 11
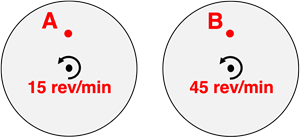
Two objects – A and B – are located halfway from the center to the outer edge of two different rotating turntables. Each turntable has the same radius but a different turning rate. Which object has the greatest linear velocity?
Object A has the greatest linear velocity.
Object B has the greatest linear velocity.
Both objects have the same linear velocity.
Questions 12
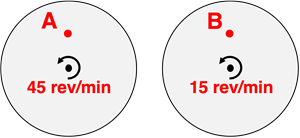
Two objects – A and B – are located halfway from the center to the outer edge of two different rotating turntables. Each turntable has the same radius but a different turning rate. Which object has the greatest linear velocity?
Object A has the greatest linear velocity.
Object B has the greatest linear velocity.
Both objects have the same linear velocity.
Question Group 4
Questions 13
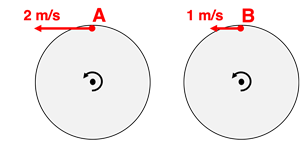
Two objects – A and B – are located on the outer edge of two different rotating turntables, each having the same radius but a different turning rate. The linear velocity of each object is shown. Which object has the greatest angular velocity?
Object A has the greatest angular velocity.
Object B has the greatest angular velocity.
Both objects have the same angular velocity.
Questions 14

Two objects – A and B – are located on the outer edge of two different rotating turntables, each having the same radius but a different turning rate. The linear velocity of each object is shown. Which object has the greatest angular velocity?
Object A has the greatest angular velocity.
Object B has the greatest angular velocity.
Both objects have the same angular velocity.
Questions 15
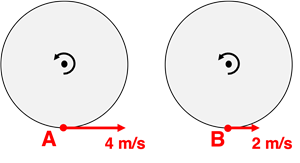
Two objects – A and B – are located on the outer edge of two different rotating turntables, each having the same radius but a different turning rate. The linear velocity of each object is shown. Which object has the greatest angular velocity?
Object A has the greatest angular velocity.
Object B has the greatest angular velocity.
Both objects have the same angular velocity.
Questions 16
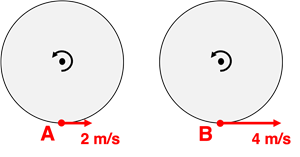
Two objects – A and B – are located on the outer edge of two different rotating turntables, each having the same radius but a different turning rate. The linear velocity of each object is shown. Which object has the greatest angular velocity?
Object A has the greatest angular velocity.
Object B has the greatest angular velocity.
Both objects have the same angular velocity.
Activity 2: Case Studies
Question Group 5
Questions 17
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and spin rates. The circle radius (R) and spin rate (in rev/min) for Case A and Case B are shown. How does the linear velocity of the two buckets compare to one another?
The linear velocity in Case A is ______ the linear velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 18
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and spin rates. The circle radius (R) and spin rate (in rev/min) for Case A and Case B are shown. How does the linear velocity of the two buckets compare to one another?
The linear velocity in Case A is ______ the linear velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 19
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and spin rates. The circle radius (R) and spin rate (in rev/min) for Case A and Case B are shown. How does the linear velocity of the two buckets compare to one another?
The linear velocity in Case A is ______ the linear velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 20
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and spin rates. The circle radius (R) and spin rate (in rev/min) for Case A and Case B are shown. How does the linear velocity of the two buckets compare to one another?
The linear velocity in Case A is ______ the linear velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Question Group 6
Questions 21
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 22
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 23
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 24
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Question Group 7
Questions 25
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 26
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 27
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 28
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Question Group 8
Questions 29
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 30
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 31
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 32
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Question Group 9
Questions 33
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 34
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 35
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 36
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and linear velocities. The circle radius (R) and linear velocity (v) for Case A and Case B are shown. How does the angular velocity of the two buckets compare to one another?
The angular velocity in Case A is ______ the angular velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Question Group 10
Questions 37
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and spin rates. The circle radius (R) and spin rate (in rev/min) for Case A and Case B are shown. How does the linear velocity of the two buckets compare to one another?
The linear velocity in Case A is ______ the linear velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 38
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and spin rates. The circle radius (R) and spin rate (in rev/min) for Case A and Case B are shown. How does the linear velocity of the two buckets compare to one another?
The linear velocity in Case A is ______ the linear velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 39
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and spin rates. The circle radius (R) and spin rate (in rev/min) for Case A and Case B are shown. How does the linear velocity of the two buckets compare to one another?
The linear velocity in Case A is ______ the linear velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Questions 40
In the World Peace Lab, a bucket filled with peas is whirled in a horizontal circle with varying radii and spin rates. The circle radius (R) and spin rate (in rev/min) for Case A and Case B are shown. How does the linear velocity of the two buckets compare to one another?
The linear velocity in Case A is ______ the linear velocity in Case B.
the same as
two times greater than
four times greater than
two times less than
four times less than
Activity 3: Do the Math
Question Group 11
Questions 41
The outermost tip of a fan blade revolves in a 1.4-meter diameter circle, making 20 complete revolutions in 30 seconds. Which expression must be used to determine the angular velocity of the tip of the fan blade in radians per second?
20 • 2 • π • 1.4 / 30
20 • 2 • π / 30
20 • π • 1.4 / 30
π • 1.4 / 30
20 • π / 30
Questions 42
The outermost tip of a fan blade revolves in a 1.6-meter diameter circle, making 15 complete revolutions in 20 seconds. Which expression must be used to determine the angular velocity of the tip of the fan blade in radians per second?
15 • 2 • π • 1.6 / 20
15 • 2 • π / 20
15 • π • 1.6 / 20
π • 1.6 / 20
15 • π / 20
Questions 43
The outermost tip of a fan blade revolves in a 1.2-meter diameter circle, making 40 complete revolutions in 60 seconds. Which expression must be used to determine the angular velocity of the tip of the fan blade in radians per second?
40 • 2 • π • 1.2 / 60
40 • 2 • π / 60
40 • π • 1.2 / 60
π • 1.2 / 60
40 • π / 60
Question Group 12
Questions 44
The blades of a windmill rotate in a circle, making 20 revolutions per minute. The outer tip of each blade is 4.0 meters from the circle's center. Which expression must be used to determine the linear velocity of the blade's outer tip in meter per second?
4.0 • 20 • π / 60
2 • π • 4.0 / 60
20 • 2 • π / 60
20 • 2 • π • 4.0 / 60
20 • 4.0 / 60
Questions 45
The blades of a windmill rotate in a circle, making 15 revolutions per minute. The outer tip of each blade is 5.0 meters from the circle's center. Which expression must be used to determine the linear velocity of the blade's outer tip in meter per second?
5.0 • 15 • π / 60
2 • π • 5.0 / 60
15 • 2 • π / 60
15 • 2 • π • 5.0 / 60
15 • 5.0 / 60
Questions 46
The blades of a windmill rotate in a circle, making 10 revolutions per minute. The outer tip of each blade is 6.0 meters from the circle's center. Which expression must be used to determine the linear velocity of the blade's outer tip in meter per second?
6.0 • 10 • π / 60
2 • π • 6.0 / 60
10 • 2 • π / 60
10 • 2 • π • 6.0 / 60
10 • 6.0 / 60
Question Group 13
Questions 47
A flywheel having a radius of 20 cm has a spin rate of 12 revolutions per second. Which expression must be used to determine the angular velocity of the flywheel in radians per second?
12 • 2 • π • 20
12 • 2 • π • 20 / 100
12 • 20
12 • 2 • π
12 • 20 / 2 / π
Questions 48
A flywheel having a radius of 15 cm has a spin rate of 10 revolutions per second. Which expression must be used to determine the angular velocity of the flywheel in radians per second?
10 • 2 • π • 15
10 • 2 • π • 15 / 100
10 • 15
10 • 2 • π
10 • 15 / 2 / π
Questions 49
A flywheel having a radius of 24 cm has a spin rate of 8 revolutions per second. Which expression must be used to determine the angular velocity of the flywheel in radians per second?
8 • 2 • π
8 • 2 • π • 24
8 • 2 • π • 24 / 100
8 • 24
8 • 24 / 2 / π
Question Group 14
Questions 50
A turntable has an angular velocity of 2.5 radians/second. A lady bug is positioned 0.20 m from the turntable's center (and nobody knows why). Which expression must be used to determine the linear velocity of the lady bug in meter/second?
2.5 • 2 • π / 0.20
2 • π / 0.20
2.5 • 0.20
2.5 • 2 • π • 0.20
2.5 • 2 • π • 0.20 / 360
Questions 51
A turntable has an angular velocity of 3.0 radians/second. A lady bug is positioned 0.16 m from the turntable's center (and nobody knows why). Which expression must be used to determine the linear velocity of the lady bug in meter/second?
3.0 • 2 • π • 0.16
3.0 • 2 • π / 0.16
3.0 • 0.16
2 • π / 0.16
3.0 • 2 • π • 0.16 / 360
Questions 52
A turntable has an angular velocity of 4.0 radians/second. A lady bug is positioned 0.12 m from the turntable's center (and nobody knows why). Which expression must be used to determine the linear velocity of the lady bug in meter/second?
4.0 • 2 • π • 0.12
4.0 • 2 • π / 0.12
4.0 • 0.12
2 • π / 0.12
4.0 • 2 • π • 0.12 / 360