Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 2: Gas Laws
Part g: Dalton's Law of Partial Pressure
Part a: Pressure and Temperature
Part b: Volume and Temperature
Part c: Pressure and Volume
Part d: Volume and the Number of Moles
Part e: The Ideal Gas Law
Part f: Combined Gas Law
Part g: Dalton's Law of Partial Pressure
Part h: Graham's Law of Effusion
Gas Mixtures
Our discussion in Lesson 2 has pertained to gases of pure substances. But what if the sample of gas is a mixture of several gases? The most common gas to us earthlings is air - a mixture of nitrogen, oxygen, argon, and other trace substances. Do the gas laws for pure substances apply equally to gas mixtures like air?
Dalton’s Law
John Dalton, whom we first met in Chapter 3 during our introduction to atomic theory, proposed a law regarding gas mixtures. Dalton’s Law can be stated as …
The total pressure of a gas mixture is the sum of the pressure that each individual gas would exert if it were alone in a container having the same temperature and pressure.
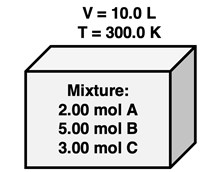
Suppose that we have a mixture of gases A, B, and C in a container with a volume of 10.0 L at a temperature of 300.0 K. There are 2.00 mol of A, 5.00 mol of B, and 3.00 mol of C in the mixture. If each of these individual gases were in their own 10.0-L container at 300.0 K, then we could use the ideal gas law to determine their individual pressures. This is shown below.
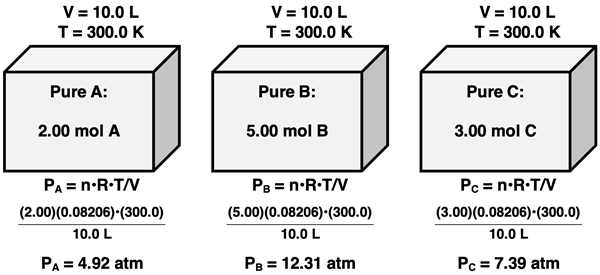
Each gas exerts a pressure of its own when its present in its own container of the same volume and at the same temperature. When all three gases are added together to form the mixture, the pressure that they exert does not change, provided that the volume and temperature are held constant. According to Dalton’s Law, the total pressure of the gas mixture is the sum of the individual gas pressures:
PTotal = PA + PB + PC
PTotal = 4.92 atm + 12.31 atm + 7.39 atm
PTotal = 24.62 atm
Dalton’s Law says that summing the individual pressures of each gas gives the total pressure of the mixture. In effect, a gas mixture acts as if there is no mixture; there’s just gas particles. And the total pressure can be determined by considering every gas particle, whether it is A, B, or C, as contributing to the total pressure. We would get the same result for the total pressure if we assumed that there were 10.00 mol of generic gas (10.00 mol is the sum of the mole amounts of the three different gases). At 300 K in a 10.0 L container, the pressure of 10.00 mol of gas would be …
PTotal = nTotal•R•T/V
PTotal = (10.00 mol)•(0.08206)•(300)/(10.0)
PTotal = 24.62 atm
Partial Pressures and Mole Fractions
In a gas mixture, each individual gas contributes to the total pressure. Conceptually, you can think of particles of Gas A colliding with container walls and contributing to the overall pressure. Gas B and Gas C also contribute to the overall pressure. We refer to the contribution that each gas makes as the partial pressure of that individual gas. In the equation
PTotal = PA + PB + PC,
PA, PB, and PC are the partial pressures of gases A, B, and C. The total pressure is the sum of the partial pressures.
The manner in which we calculate the partial pressure of gas A and the total pressure of the mixture is shown below.
If we divide PA by PTotal and do some algebraic clean-up, we get
The ratio of nA/nTotal is referred to as the mole fraction of A and is represented by ΧA. The mole fraction of A indicates the fraction of the total moles of the mixture that identify as substance A. We can rearrange the equation to state PA = ΧA •PTotal. Put in words, this says that the partial pressure of Gas A is the total pressure of the mixture multiplied by the mole fraction of A. That which is true for Gas A is also true for Gas B and Gas C … and any individual gas in the mixture. Each individual gas contributes to the total pressure and the extent of the contribution is proportional to the mole fraction (Χ) of that individual gas in the mixture.
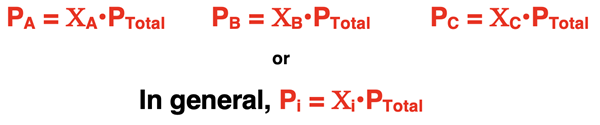
Example 1
A 30.0 L container of argon gas has a pressure of 24.8 atm. An identical container of neon gas at the same temperature has as pressure of 6.2 atm. The two gases are added to a third 30.0-L container that has the same temperature. Determine the total pressure of the gas mixture and the mole fraction of the argon and neon in the mixture.
Tap the Check Answer button to view the answer and explanation.
Mixing Gases
So far, we have seen equal volumes of gases being mixed into containers of the same volume. This isn’t always the case and Dalton’s Law can be used in situations in which unequal volumes of gases are mixed. The law simply states that
The total pressure of a gas mixture is the sum of the pressure that each individual gas would exert if it were alone in a container having the same temperature and pressure.
If unequal volumes are mixed, it is important to perform a gas law calculation to determine the volume an individual gas would have if it were in a container of the same volume and temperature as the mixture.
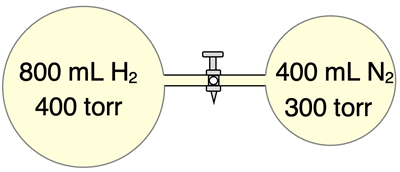
Suppose two flasks of different volumes are filled with hydrogen and nitrogen gas as shown. A closed valve prevents the gases from mixing. Once the valve is opened, the two gases diffuse to fill both containers and uniformly mix. The final volume can be assumed to be 1200 mL. We wish to determine the partial pressures of the hydrogen and nitrogen gases and the total pressure of the mixture. We will assume that there is no change in temperature.
In this instance, each individual gas is undergoing an expansion from its original volume to a final volume of 1200 mL. There is no change in temperature or change in the number of moles of the individual gas as the result of the volume change. Boyle’s Law, P1•V1 = P2•V2, can be used to determine the pressure (P2) that each individual gas would have if its volume were 1200 mL (V2). These calculations are shown below.
Hydrogen:
Known:
P
1 = 400 torr
V
1 = 800 mL
V
2 = 1200 mL
Find: P
2 = ????
Use P
2 = P
1•V
1 / V
2
Substitute and Solve:
P
2 = (400 torr)•(800 mL) / (1200 mL)
P
2 =
PHydrogen = 267 torr (rounded from 266.666…)
Nitrogen:
Known:
P
1 = 300 torr
V
1 = 400 mL
V
2 = 1200 mL
Find: P
2 = ????
Use P
2 = P
1•V
1 / V
2
Substitute and Solve:
P
2 = (300 torr)•(400 mL) / (1200 mL)
P
2 =
PNitrogen = 100 torr
Our calculations show that each individual gas, if present in a 1200 mL container at the same temperature as the mixture would have partial pressures of roughly 267 torr and 100 torr. Thus, the total pressure is the sum of the partial pressures.
The total pressure is roughly 367 torr.
Example 2
Unequal volumes of He and Ne gas mix when the valve is opened. The gases diffuse through the entire two-flask system to form a gas mixture with a final volume of 4.00 L. Assuming no temperature change, determine the partial pressures of He and Ne in the mixture, the mole fractions of He and Ne, and the total pressure of the gas mixture.
Tap the Check Answer button to view the answer and explanation.
Wet Gases
A common lab procedure involves collecting a gas in an inverted, water-filled cylinder. The cylinder is initially filled with water and then inverted and placed in a large beaker of water. Typically, a reaction that generates a gas occurs in the bottom of the cylinder. As the gas is produced, it bubbles upwards towards the top of the cylinder. The gas displaces the water at the top of the inverted cylinder and pushes the water downward. The cylinder is often calibrated allowing for a measurement of the volume of gas produced by the reaction.
The gas formed at the top of the cylinder is actually a gas mixture. It is often referred to as a wet gas. The adjective wet indicates that water is present in the gas. If the reaction produces hydrogen gas, then the gas mixture is a combination of hydrogen and water. The water is present in the mixture because water, like any liquid, has a vapor pressure. There is always a small amount of evaporated water above any sample of liquid water. The amount is dependent upon the temperature of the liquid water, with increasing amounts of vapor present at higher temperatures. The vapor pressure of the water can be used as the partial pressure of the water in the mixture. The pressure of the room can be used as the pressure of the gas mixture. Dalton’s Law must be used to determine the pressure of the collected gas.
As an example, suppose that hydrogen gas is collected above water at a temperature of 25°C and a room pressure of 745 mm Hg. The vapor pressure of water at 25°C is 24 mm Hg. The pressure of the hydrogen gas is determined using Dalton’s Law:
PTotal = PHydrogen + PWater
where PTotal = 745 mm Hg and PWater = 24 mm Hg
745 mm Hg = PHydrogen + 24 mm Hg
PHydrogen = 721 mm Hg
Example 3
A sample of hydrogen gas is collected in a eudiometer tube over water at a temperature of 30.0°C and a total pressure of 744.8 mm Hg. The vapor pressure of water is 31.8 mm Hg. If the volume of the gas in the eudiometer tube is 46.18 mL, then determine the number of moles of hydrogen that have been collected.
Solution:
In this example, temperature, volume, and pressure information is given and we wish to determine the number of moles of hydrogen gas. This is an ideal gas law problem. But because the hydrogen gas is collected over water, it is a wet gas. That is, it is a mixture of hydrogen gas and water vapor. Dalton’s Law must be used to determine the pressure of the hydrogen gas. Once determined, the ideal gas law can be used to determine the number of moles.
Dalton’s Law:
PTotal = PHydrogen + PWater
where PTotal = 744.8 mm Hg and PWater = 31.8 mm Hg
744.8 mm Hg = PHydrogen + 31.8 mm Hg
PHydrogen = 713.0 mm Hg
Ideal Gas Law:
We know the following for hydrogen:
P = 713.0 mm Hg ==> (Divide by 760.0 to convert to atm) ==> 0.9381578 …. atm
V = 46.18 mL ==> (Divide by 1000 to convert to L) ==> 0.04618 L
T = 30.0°C ==> (Add 273.15 to convert to Kelvin) ==> 303.15 K
We can use P•V = n•R•T to calculate the number of moles (n).
n = P•V/(R•T) = (0.9381578 …. atm)•( 0.04618 L)/ [ (0.08206 L•atm/mol/K)•( 303.15 K) ]
n = 0.001742 mol H2 (rounded from 0.001741569 … )
Conclusion
Dalton’s Law is the go-to gas law for analyzing gas mixtures. As we have seen on this page, it is often used with other gas laws like Boyle’s Law and the Ideal Gas Law. We are nearing the end of our gas laws lesson. Next up is Graham’s Law. But before you move onward, please check out our learning suggestions below.
Before You Leave
- Download our Study Card on Dalton’s Law. Save it to a safe location and use it as a review tool. (Coming Soon.)
- Problem Set GL12 in our Calculator Pad section provides six awesome practice problems. Visit Problem Set GL12: Dalton's Law of Partial Pressures.
- The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1. Two different 10.0 L containers at the same temperature are filled with helium at a pressure of 23.8 psi and neon at a pressure of 17.2 psi. The neon gas is added to the helium container.
- What is the total pressure of the mixture in the third container?
- What is the mole fraction of the two gases in the third container?
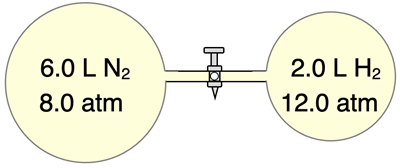
2. Unequal volumes of N2 and H2 gas mix when the valve is opened. The gases diffuse through the entire two-flask system to form a gas mixture with a final volume of 8.0 L. Assuming no temperature change, determine the partial pressures of N2 and H in the mixture, the mole fractions of N2 and H2, and the total pressure of the gas mixture.
3. Would your answer to Problem #2 be any different if the gases were Cl2 and CH4? Explain your thinking.
4. Would the total pressure of the container (once the gases are mixed) be any different if both flasks were filled with the same gas? Explain your thinking.