Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Force on a Wire in Magnetic Fields
In the previous lesson, we learned that when a charged particle moves through a magnetic field that points perpendicular to the direction of motion, the charge feels a magnetic force. In this lesson, we’ll see that the same is true for a current-carrying wire in a magnetic field. We also learned in the previous lesson that scientists can use this information about the magnetic force to determine a particle’s charge and mass. This is how particle physicists discovered subatomic particles and how scientists determine the atomic mass of the elements that make up the periodic table. We might ask ourselves, “Are there any applications of using the result that a current-carrying wire feels a force in a magnetic field?” Truth is, there are hundreds of applications to this physics principle! We’ll explore the motor and the speaker as two significant applications of this principle after we understand what this magnetic force depends on and how we can know its direction.
Let’s begin by drawing a parallel between the force on a moving charge and the force on a current-carrying wire. It is no coincidence that one follows from the other when we recall that current is just the rate at which charges move through a wire. Beginning with the equation for the force on a moving charge in a magnetic field, we derive a new equation—an equation for the force on current-carrying wire in a magnetic field.

Start with equation for magnetic force on a moving charge: F = q v B. Writing velocity as length per time, we gett F = q times (L over delta t) times B. Rewrite this F = L times B times q over t. Recall that charge per time is current (q over t), so we replace that with I, and get F = I L B or Force (F) = Current (I) times Length (L) times Perpendicular Magnetic Field (B)
Putting these two equations side by side, we see similarities. Just like a faster moving charge results in a bigger magnetic force, a larger current yields a larger force. Both require the magnetic field to be perpendicular to the moving charge or current to produce this magnetic force.

Example 1: A Current-Carrying Wire in a B-Field
Problem: A wire carries a current of 4.0 Amps in a 0.60 T magnetic field as shown. If 45 cm of the wire is in the magnetic field, determine the magnitude of the force on this wire.
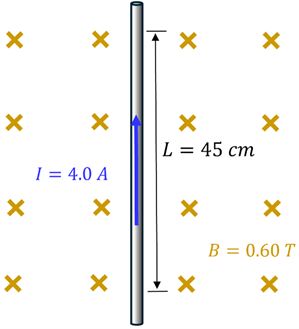
Solution: We apply the equation for magnetic force on a current-carrying wire. Since the field is already perpendicular to the direction of current, we can simply multiply these three quantities—being sure to convert the length to meters.
F = I L B⟂
F = (4.0 A)(0.45 m)(0.60 T)
F = 1.08 N (rounded to 1.1N)
Example 2: When B-field is not Perpendicular
A wire carries 2.0 A of current in the wire that makes a 70o angle with respect to a 150 mT magnetic field. The magnetic field is confined to a region that is 120 cm high, with no field above or below this region. Determine the magnetic force on the wire.
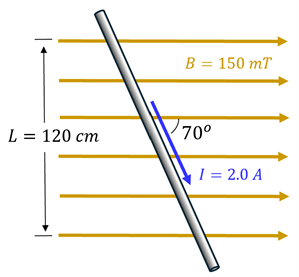
Solution: When the angle between the current-carrying wire and the B-field is not 90o, we need to find either the component of the B-field that is perpendicular to the length of wire in the field, or the length of the wire that is perpendicular to the B-field. Both will give us the same results. Since, however, the component of the length of wire that is perpendicular to the field is the length shown, we can simply calculate the force in this manner. Thus, the 70o angle is not needed in this calculation (1.277 m * sin(70) = 1.2 m). Just recall that 150 mT is 0.15 T.
F = I L B⟂
F = (2.0 A)(1.20 m)(0.15 T)
F = 0.36 N
The 'Force-Finding' Right Hand Rule
In the previous lesson, we learned the Force-finding Right Hand Rule that allowed us to find the direction of the force on a moving charge in a B-field. Is there a similar rule that allows us to find the direction of the force on a current-carrying wire? Indeed, there is! In fact, you’ll see the striking similarities continue.
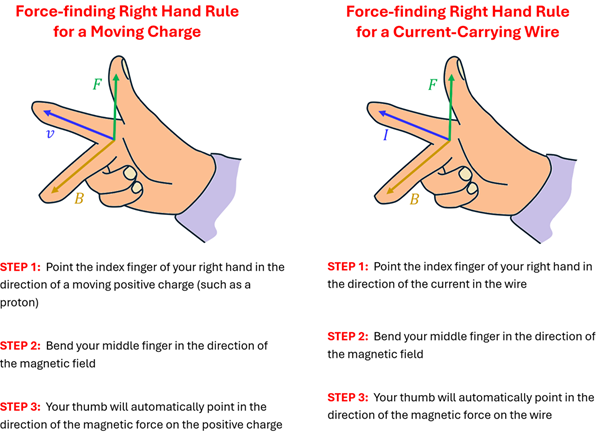
So far in this chapter we’ve learned two different right hand rules: (1) the Field-finding Right Hand Rule, and (2) the Force-finding Right Hand Rule. The first rule allowed us to find the magnetic field around a current-carrying wire. We saw that electricity causes magnetism. This second rule allows us to find either the force on a moving charge or on a wire that carries current in an external magnetic field. We say ‘external field’ here because the field created by a current-carrying wire cannot exert of force on itself. However, the B-field created by a nearby current-carrying wire can exert a force on another current-carrying wire. While Example 3 will focus on the Force-finding Right Hand Rule for current-carrying wires, we’ll see in Example 4 how this works when we combine it with the Field-finding Right Hand Rule for current-carrying wires.
Example 3: Finding direction of the Force on Current-Carrying Wire in a B-Field
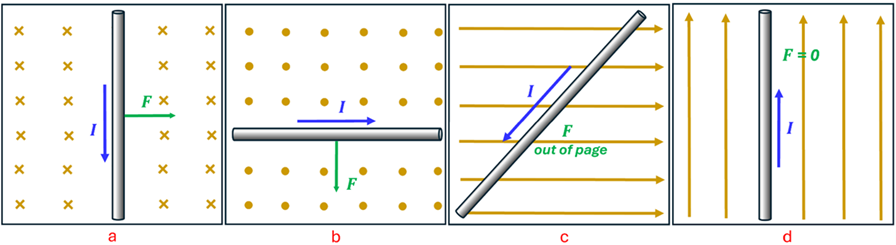
Problem: Use the Force-finding Right Hand Rule to predict the direction of the force on the current-carrying wire in each of these situations.
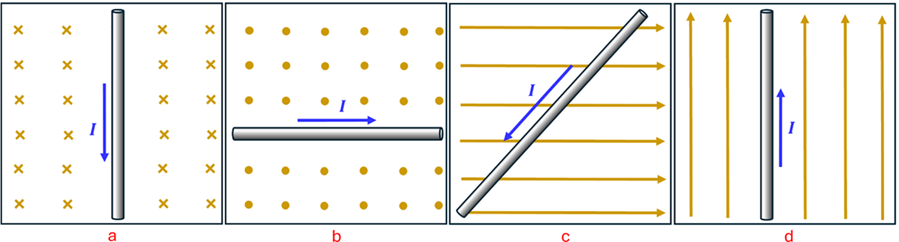
Solution: To apply the Force-finding Right Hand Rule in situation ‘a’, we point the index figure toward the bottom of the page—in the direction of the current. That is Step 1. Now, keeping your index finger pointing in that direction, rotate your hand so that you can bend your middle finger in the direction of the B-field—which is into the page. That is Step 2. If you’ve done this correctly, your thumb should be pointing toward the right. That is Step 3 and represents the direction of the magnetic force on this current-carrying wire.
For situation ‘b’, the magnetic field is pointing out of the page. This should allow you to see that the force on this current-carrying wire is toward the bottom of the page. For situation ‘c’, you point your index finger in the direction of the current. While the magnetic field is not perpendicular to the current, you can bend your middle finger a little more than 90o so that it is pointing in the direction of the B-field. This will still allow you to find the direction of the force. Doing so will results in your thumb pointing out of the page. This is the direction of the force. Finally, for situation ‘d’, there is no component of the magnetic field perpendicular to the current. For this situation there is no force that acts on the wire.
The “Field-finding Right Hand Rule” that we learned in a previous lesson allows us to find the direction of the magnetic field around a current-carrying wire. The “Force-finding Right Hand Rule that we have just introduced in this lesson, allows us to find the direction of the magnetic force on a current-carrying wire. As we mentioned above, it is possible that the B-field produced by one wire can create the magnetic field that causes a force on a second current-carrying wire. Now that you are becoming a pro at both rules, let’s consider a few situations where we put the two right hand rules together.
Example 4: Putting the Two Right Hand Rules Together
Problem: For (a) and (b), determine the direction of the force on wire 2 due to wire 1. For (c), determine the path of the positive charge due to the field of the current-carrying wire.
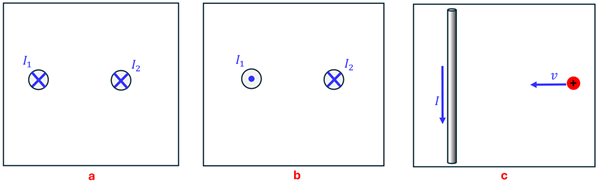
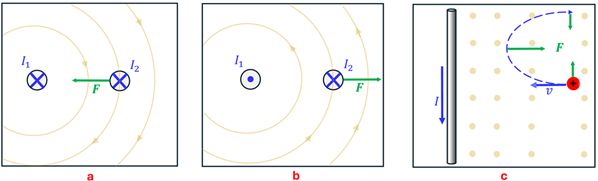
Solution: For case (a), wire 2 will feel a force toward wire 1. Why is this the direction of the force? First, we’ll use the “Field-finding Right Hand Rule” to determine the direction of the B-field around wire 1. Do you see that the field created by wire 1 is pointing toward the bottom of the page at the location of wire 2? With the direction of the B-field established, now let’s apply the “Force-finding Right Hand Rule” for wire 2 knowing that the magnetic field—the one created by wire 1—is pointing downward. The result is that wire 2 feels a force to the left. In fact, whenever two current-carrying wires carry current in the same direction, they are attracted one another. For case (b), we see that the B-field due to wire 1 in the vicinity of wire 2 is pointing toward the top of the page. Now, using the “Force-finding Right Hand Rule,” we see that wire 2 feels a force to the right. It follows that whenever two parallel wires carry current in opposite directions, they feel a force away from each other. For case (c), we see that the current-carrying wire produces a magnetic field that points out of the page anywhere to the right of this wire. Thus, using the “Force-finding Right Hand Rule” we see that a positive charge that is approaching the wire will feel a force directed upward such that it bends in an arc as shown. Notice that, since the magnetic field gets stronger as the charge gets closer to the wire, the arc is not perfectly circular. How did you do? Are you getting these? Give yourself a hand…a right hand, that is!
Applications of Current-Carrying Wires in B-Fields
We mentioned above that there are many applications where having a force applied to a current-carrying wire in a magnetic field is advantageous. Since Oersted’s discovery back in 1820, engineers have created hundreds of devices that work because of the connections between electricity and magnetism. Applications that take advantage of a current-carrying wire feeling a force when in a magnetic field range from speakers, to motors, to magnetic levitation trains, to galvanometers, to many, many more devices.
While we could explore each of these in detail, we would quickly see that they all work on the same principle. So, to begin to see how useful this magnetic force on current-carrying wires actually is, let’s dive deep into just two applications that are part of devices you use every day—the speaker and the motor. That’s where we’ll turn our attention in the next sections of this lesson.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1. Consider the current-carrying wire in each of these three situations as you answer the questions asked.
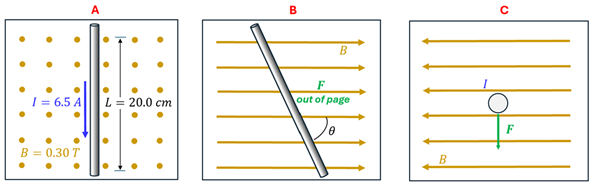
A: A wire carries 6.5 A of current across a 20 cms region that has a 0.30 Tesla magnetic field. What is the magnitude and direction of the magnetic force on the wire?
B: A 60 cm long wire carries a current of 2.0 A in a rightward pointing 1.2 T magnetic field as shown. If the force on the wire is 1.25 N out of the page, what is the angle θ that the wire makes with the B-Field? What direction is the current moving through the wire?
C: A 0.75 m long wire carries a current in a 0.050 T magnetic field as shown. If the wire feels a 0.40 N magnetic force downward, what is the magnitude and direction of the current in the wire?
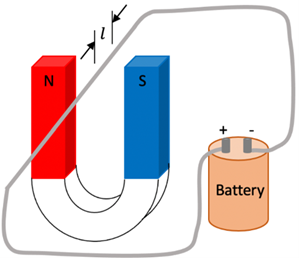
2. We learned in a previous lesson that a horseshoe magnet is useful in that it creates a relatively uniform magnetic field between its two poles. A wire carries 6.0 Amps of current when connected to the battery as shown with 4.0 cm of the wire in the magnet’s 0.08 T field. What is the magnitude and direction of the force on this wire?
3. A 30.0 cm long metal bar rests on a scale and is connected via wire to a variable power supply that controls the current through the bar. The scale reads the weight of the bar which is 2.00 N (top picture). Now, the bar is ‘bathed’ in a 0.60 T magnetic field that points into the page (bottom picture)
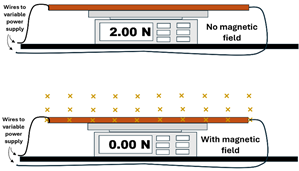
A: What current through the bar is needed so that the scale now reads 0.0 N?
B: In order for this to occur, which direction must the current flow through the bar?
Looking for additional practice? Check out the Calculator Pad for additional practice problems.