Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Forces on Moving Charges in Magnetic Fields
A fascinating branch of physics research today is called particle physics. A little over a hundred years ago scientists thought that the atom was the smallest particle that made up matter. In fact, the word "atom" comes from the Greek word "atomos" which means “indivisible” or "cannot be split." So, up until the late 1800’s, we thought the atom was a fundamental particle.
Since that time, our view of the atom has changed significantly. It was in the early 1900’s that scientists developed the understanding that an atom is made of protons, neutrons, and electrons. But are these fundamental? Could it be that they are made up of even smaller particles? This was one of the pressing questions that particle physicists in the 1900’s sought to answer. They did so (and still do!) by accelerating protons and electrons to nearly the speed of light and then colliding them with other particles. However, getting tiny particles traveling at near the speed of light to collide with one another requires steering and focusing them with great precision. How do you steer and focus a beam of such particles with pinpoint accuracy? You do so with magnets.
Physicists discovered that when a charged particle moves through a magnetic field perpendicular to its velocity, it experiences a force. This magnetic force is equal to the product of the particle’s charge, its velocity, and the component of the magnetic field that is perpendicular to its velocity. The faster the particle moves and the stronger the magnetic field, the bigger the force that will bend the trajectory of the moving charge.
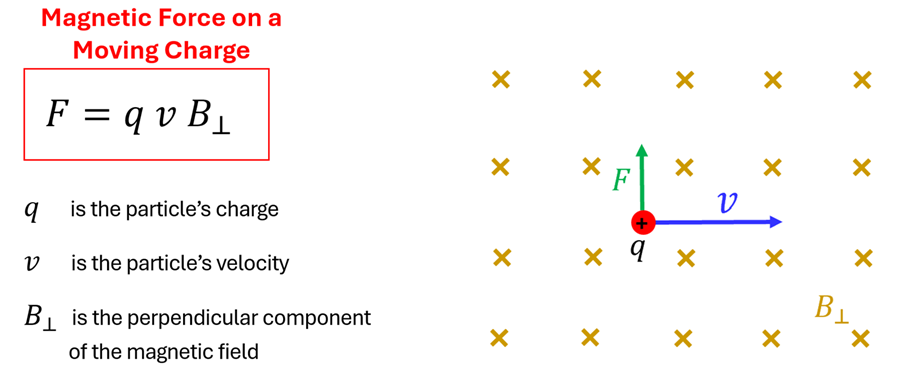
As long as the charge is measured in Coulombs (C), the velocity in meters/second (m/s), and the magnetic field in Tesla (T), the calculated force will be measured in Newtons (N). It is interesting to note, however, that it is only when the charged particle moves perpendicular to the B-field—or at least has a component of its velocity perpendicular to the B-field—that it feels this magnetic force. To help us understand just how this magnetic force is calculated, let’s consider a couple of examples.
Example 1: A Moving Electron in a B-Field
Problem: In the lab, physicists accelerate an electron to a velocity of 3.0 x 106 m/s. They direct the electron so that it enters a magnetic field of 0.50 T that is perpendicular to the direction of the moving charge. Find the magnitude of the magnetic force that acts on the electron. Use the below table as needed:
Table of Common Subatomic Particles
| Particle |
Mass (kg) |
Charge (C) |
Relative Mass |
Relative Charge |
| Proton |
1.67 x 10-27 |
+1.6 x 10-19 |
+1 |
1 |
| Electron |
9.11 x 10-31 |
-1.6 x 10-19 |
-1 |
0.0005 |
| Neutron |
1.67 x 10-27 |
0 |
0 |
1 |
Solution: The charge of an electron can be found using the above table or by search for its value online. Since we are just looking for the magnitude of the force, we can ignore the negative sign on the electron’s charge. (We’ll consider the direction of the force a bit later in this lesson). Since the charge is already in Coulombs, the velocity is in meters/second, and the magnetic field is in Tesla, the magnetic force will be in Newtons.
F = q v B⟂
F = (1.6 x 10-19C)(3.0 x 106 m/s)*(0.50 T)
F = 2.4 x 10-13 N
Example 2: The Aurora Borealis
Problem: While physicists can accelerate charged particles in the lab, nature itself acts as a particle accelerator. Solar activity on our Sun can, for example, send a spray of charged particles toward the Earth which causes the Aurora Borealis (or northern lights). Imagine that the Sun ejects a proton so that it is traveling toward the earth at a velocity of 400 km/s when it enters the Earth’s 25 µT magnetic field at an angle of 30° with respect to the field. What magnetic force does the proton experience? Use the above table as needed.
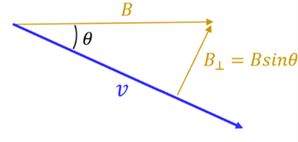
Solution: The charge of a proton can be found using the above table or by search for its value online. Next, we’ll want to convert the velocity to units of m/s. Since the velocity makes a 30° angle with respect to the magnetic field, we’ll need to find the component of the field perpendicular to the velocity. The diagram shows that B * sinθ will allow us to do this.
F = q v B⟂
F = (1.6 x 10-19C)(4.0 x 105 m/s)*[(25x10-6 T)*(sin(30°)]
F = 8.0 x 10-19 N
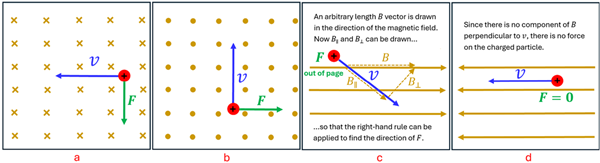
The 'Force-Finding' Right Hand Rule
Determining the magnitude of the force on a moving charge is valuable, but it is only half the story. Since force is a vector, these charges feel these forces in a predictable direction. It is this direction that allows particle physicists to steer an electron in a particle accelerator and what allows protons from the Sun to spiral around magnetic field lines and eventually enter the Earth’s atmosphere near the poles of the Earth to make the auroras. To be able to predict the direction of the force on a moving positive charge in a magnetic field, we need to understand a second right-hand rule for magnetism—the Force-finding Right Hand Rule.
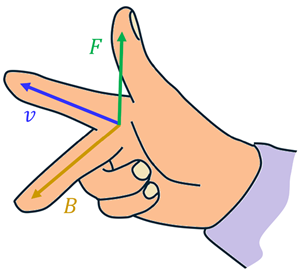
When a charged positive particle travels perpendicular to a magnetic field (or at least has a component of its velocity perpendicular to the field), it feels a force that is perpendicular to both. Here’s how it works:
Step 1: Point the index finger of your right hand in the direction of a moving positive charge (such as a proton).
Step 2: Bend your middle finger in the direction of the magnetic field.
Step 3: Your thumb will automatically point in the direction of the magnetic force on the positive charge. |
 |
What is challenging about the Force-finding Right Hand Rule is that it will ‘force’ you to visualize these quantities three-dimensionally. We’ll take advantage of the x and · symbols that we introduced back in Lesson 2 of this chapter to communicate fields that point ‘into’ and ‘out of’ the page.
Example 3: Finding Direction of the Force on Moving Positive Charges in B-Field
Problem: Use the Force-finding Right Hand Rule to predict the direction of the force on the moving positive charge in each of these situations.
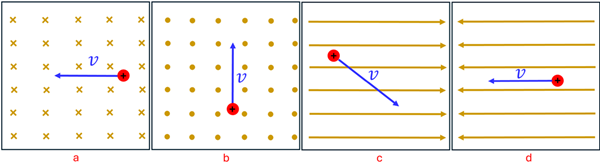
Solution: To apply the Force-finding Right Hand Rule in situation ‘a’, we point the index figure to the left of the page. That is Step 1. Now, keeping your index finger pointing in that direction, rotate your hand so that you can bend your middle finger in the direction of the B-field—which is into the page. That is Step 2. If you’ve done this correctly, your thumb should be pointing toward the bottom of the page. That is Step 3 and represents the direction of the magnetic force on this moving positive charge.
For situation ‘b’, the magnetic field is pointing out of the page. This should allow you to see that the force on this particle is to the right of the page. For situation ‘c’, you point your index finger in the direction of the velocity. While the magnetic field is not completely perpendicular to the velocity, there is a component of the B-field perpendicular to the velocity which points up and to the right. The result is that the force on this positive charge is pointing out of the page. Finally, for situation ‘d’, there is no component of the magnetic field perpendicular to the velocity. For this situation there is no force that acts on the charge.
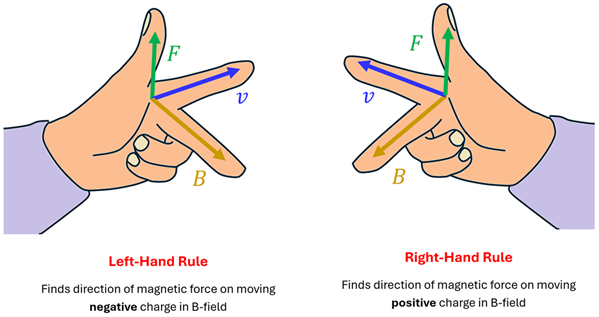
You may have noticed that we’ve limited our Force-finding Right Hand Rule to moving positive charges. That was intentional. It turns out that if we have a moving negative charge—such as an electron—it will feel a force in exactly the opposite direction. Good news, however. Your left hand works in exactly the same way to determine the direction of the magnetic force on a moving negative charge in magnetic field.
Example 4: Finding a Particle's Charge
Problem: Particle physicists are able to capture the trails left behind when particles enter a magnetic field. Three particle trails are shown for three different particles. What is the charge of each particle? How do you know?
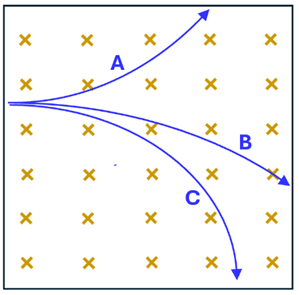
Solution: Particle A must be positively charged. Using the Force-finding Right Hand Rule, we can see that Particle A feels a force toward the top of the page as it enters the magnetic field at the left of the picture. This makes sense because the particle path bends in this direction. Particles B and C must be negatively charged. They both must feel a force toward the bottom of the page since their trajectory is one that curves downward. A downward force is explained only by using the Force-finding Left Hand Rule. Thus, Particles B and C must be negatively charged.
The Path of Moving Charges
In Example 4, we were able to determine which particle was positive and which were negatively charged by knowing the direction of the force on each. In other words, we used the fact that if a charged particle enters a magnetic field, its trajectory bends. If the particle continues in the magnetic field, it keeps bending. In fact, since the force is always perpendicular to the direction that it is moving, it will undergo circular motion. We saw in a previous lesson that circular motion is the result of a moving object feeling a force that is aways perpendicular to its velocity. Since this is exactly what we have with moving charges in magnetic fields, this is exactly what we get!
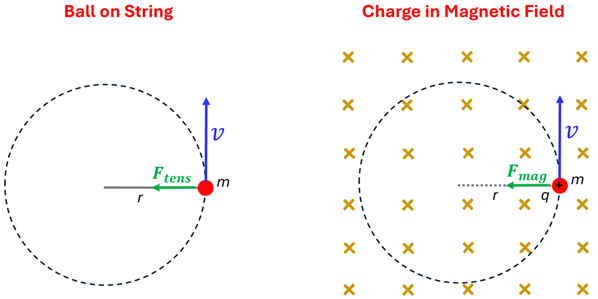
In that previous lesson, when we considered an object such as a ball spinning on the end of a string in a horizontal circle, we saw that the string does no work on the ball since the tension force is perpendicular to the direction of motion. The result is that the ball continues moving with a constant speed. The same is true of magnetic forces. While they can be used to change the direction of moving charges, they do no work on the charge and thus cannot change the particle’s speed.
It is no coincidence that the world’s largest particle accelerator located at CERN (the European Organization for Nuclear Research) is circular. This 27 km circumference beamline is located on the boarder of France and Switzerland. While the beam pipe through which protons and other ions travel is underground, the yellow circle on this aerial photo marks out the path traveled by these charges before colliding with other particles. By increasing the strength of the field at certain points along the particles’ orbit, the charges can be steered along a path that is not completely circular.

Figure 2
In this lesson we have seen how particle physicists can use magnets to not only steer charged particles but also to determine the charge of subatomic particles by observing the direction they bend in a magnetic field. But how do scientists learn about other properties of atoms and the things that make up atoms? Can a magnet be used, for example, to find the mass of these tiny particles? Indeed, it can! That is the focus of our next lesson.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1. Determine the magnitude and direction of the magnetic force acting on the given charge in each of these situations. Use the above table as needed.
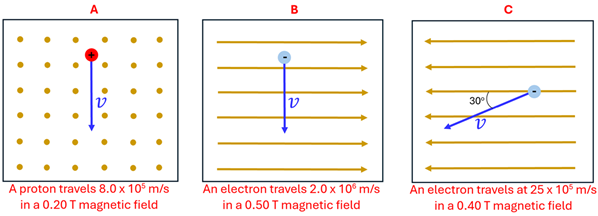
2. In a physics lab, a magnetic force of 6.2 x 10-14 N pointing toward the north wall of the laboratory acts on an electron at the instant it is moving at 8.2 x 106 m/s toward the east wall. What is the minimum magnitude and direction of the magnetic field needed to make this occur? Use the above table as needed.
3. Solar activity can send protons toward the Earth with a large velocity. When such a proton enters the Earth’s magnetic field at an angle less than 90o, a component of the Earth’s field will be perpendicular to the velocity while another component will be parallel to the proton’s velocity. The result is that the proton travels in a helical spiral as shown. Assume a proton is traveling at 240 km/s when it enters the Earth’s 25 µT magnetic field at an angle of 75o with respect to the field. (a) What magnetic force acts on the proton, and (b) why would this trajectory trace out a helix instead of just a circle? Use the above table as needed.
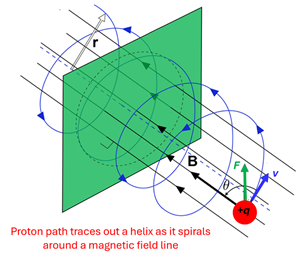
Figure 1 Source: Taken by Author's Daughter 2024 in Canada
Figure 2 Source: https://commons.wikimedia.org/wiki/File:CERN_Aerial_View.jpg (left) and https://commons.wikimedia.org/wiki/File:CMS_img_0493.jpg (right)