Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 3: Gas Stoichiometry
Part b: Gas Stoichiometry at Standard Conditions
Part a: Stoichiometry Revisited
Part b: Gas Stoichiometry at Standard Conditions
Part c: Gas Stoichiometry at Non-Standard Conditions
Coefficients and Volume Ratios
We learned in Chapter 9 of our Chemistry Tutorial that the coefficients of a balanced chemical equation indicate the mole ratios. That is, they indicate the relative number of moles of reactants and products involved in the chemical reaction. We learned of Avogadro’s Law in Lesson 2 of this chapter. There are two relevant aspects of the law that pertain to stoichiometry. First, equal volumes of different gases at the same temperature and pressure contain the same number of moles. Second, the ratio of volume to moles will be a constant ratio at the same temperature and pressure. When these two ideas are combined, we can reason that the coefficients in the balanced chemical equation act as volume ratios for any two or more reactants and/or products that exist in the gaseous state.
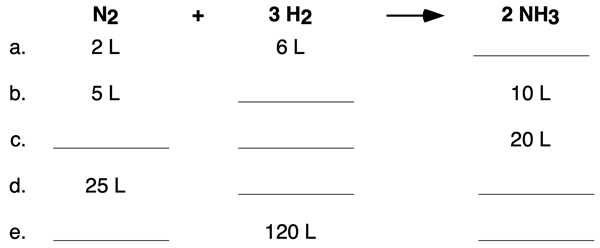
In the ammonia synthesis reaction …
N2(g) + 3 H2(g) → 2 NH3(g)
… all reactants and products are in the gas state. The coefficients indicate volume ratios. So, 1 L of N2 gas would react with 3 L of H2 gas to produce 2 L of NH3 gas. Knowing the volume of a reactant would allow us to predict the volume of the other reactant or the product. Coefficients are used to convert from volume of one reactant to the volume of a product and vice versa.
Suppose 15.8 L of N2 react to produce ammonia (NH3). How much hydrogen would react with it? And how much ammonia would be produced? To determine the answers to these questions, the coefficients of the equation can be turned into volume ratios (like mole ratios but listing liters instead of moles). The factor label method is then used to convert from L N2 to the volume of H2 and of NH3.
Example 1
Use volume ratios to determine the volumes of reactants and products for five trials of the ammonia synthesis reaction. When done, tap the Check Answer button to view all the answers.
What’s So Special About STP?
We learned in Lesson 2 that the volume of a gas is dependent upon temperature and the pressure. Numerous industries sell and purchase gases in a cylinder. Suppose a company needs to purchase a 30-liter cylinder of helium gas. The moles of gas in the cylinder depends on the pressure and temperature of the gas when it was added to the cylinder. A 30-liter container could contain a small number of moles (n) if prepared at a low pressure and/or a high temperature. Or it could contain a large number of moles (n) if prepared at a high pressure and/or a low temperature. So, to standardize the discussion of the amount of gas that is being sold and purchased, a standardized temperature and pressure is used. That standard is known as STP. Standard temperature is 273.15 K and standard pressure is 1.00 atm. The volume of the gas at STP is stated so that the consumer can know exactly how many moles of gas is being purchased.
In Chemistry class, we know the volume occupied by 1.00 mole of gas at STP. For an ideal gas, the volume of 1.00 mole at STP is 22.4 L. You can count on it! This quantity is known as the molar volume. At standard conditions (STP), it can be used to determine the moles of gas if given the volume or the volume of gas if given the moles.
Molar Volume and Stoichiometry
Using coefficients as volume ratios works for gaseous reactants and products. But if a reaction includes a solid, liquid, or aqueous-state substance, then a volume-to-volume conversion is not possible for that substance. Consider the reaction for the electrolysis (or decomposition) of liquid water.
2 H2O (l) → 2 H2(g) + O2(g)
The coefficients indicate that 2 mol of liquid H2O decompose to form 2 mol of H2 gas and 1 mol of O2 gas. The volume of the two gaseous products at STP conditions can be determined by using the molar volume. The 2 mol of H2 at STP would have a volume of 44.8 L (twice the 22.4 L for one mol). The 1 mol of O2 has a volume of 22.4 L. So, we could say that 2 mol of liquid H2O decompose to form 44.8 L of H2 gas and 22.4 L of O2 gas. This statement involves two steps of logic:
- A mole ratio is used to convert from moles of reactant to moles of a product.
- A molar volume is used to convert from moles of a product to liters at STP.
The factor label method is often used to perform the conversions for STP conditions. The equivalence statement is
22.4 L = 1 mole (for gases at STP)
The following two conversion factors can be made from this equivalence statement:
Rethinking Mole Island for Gases
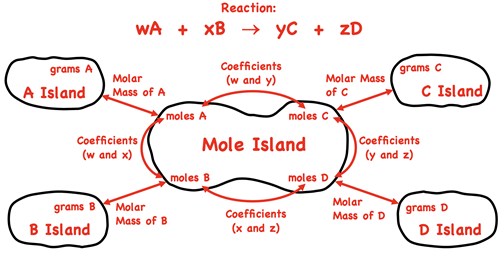
We introduced a graphic organizer known as Mole Island in our Stoichiometry chapter. The graphic organizer displays the various How much? quantities - grams and moles of reactants and products. The arrows between quantities indicate what is related to what and how it is related. For instance, the grams of A is related to the moles of A by the molar mass. And the moles of A are related to the moles of C by the coefficients in front of A and C. The graphic organizer is a tool for navigating your way through a stoichiometry problem. To use the graphic, identify the given quantity on the diagram. Then identify the desired quantity. Finally use the arrows and the information about the arrows to determine how many conversion factors are involved and what information (molar mass or coefficients) is used to form the conversion factors.
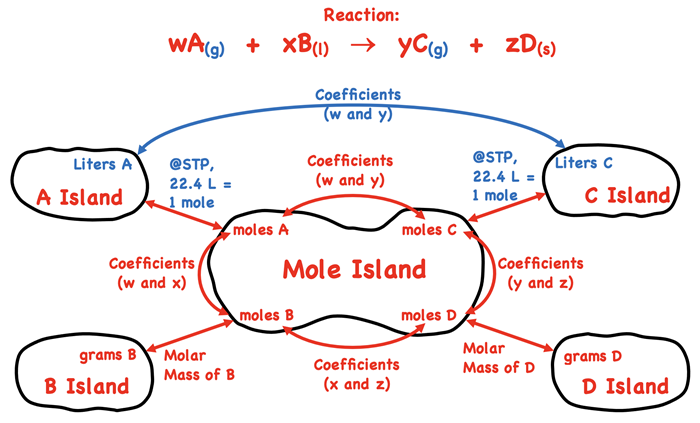
As discussed on the previous page, gas stoichiometry introduces new How much? quantities into a stoichiometry problem. The volume, pressure, and temperature conditions of reactants and products are the new quantities. They apply to gaseous reactants and products only. We have done a mild revision to the Mole Island graphic to account for the possibility of gases. Our revisions are displayed in blue below.
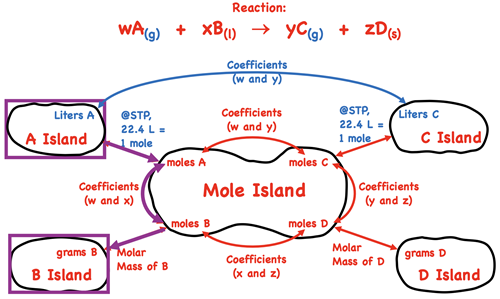
Let’s discuss a generic example to illustrate how to use Mole Island to navigate your path through a stoichiometry problem. Suppose that you are given the volume of substance A (a gas) at STP conditions and asked to calculate the mass of substance B (a liquid). How would you proceed? How many conversion steps are involved and what information is used to perform the conversions? To answer such a question, begin by identifying the starting point (the given quantity) and the final destination (the desired quantity) on the diagram. This is done using purple boxes. There are three arrows between the starting point and the final destination. Thus, the problem will use three conversion factors. The first conversion factor will involve the molar volume a gas at STP. The second conversion factor will involve coefficients from the balanced equation. The third and final conversion factor will involve the molar mass of substance B.
Example 2
Solid titanium(IV) nitride is synthesized from solid titanium and nitrogen gas.
3 Ti(s) + 2 N2(g) → Ti3N4(s)
Determine the volume of nitrogen at STP that is needed to react with 17.8 g of Ti.
Solution:
We have customized our Mole Island graphic for this reaction, replacing the generic reaction with the actual reactants and products. We have also used purple rectangles to identify the starting point (grams of Ti on Ti Island) and the final destination (Liters N2 on N2 Island).
As can be seen, there are three arrows between the starting point and the final destination. Three conversion factors are needed. The conversion factors, in order, will use the molar mass of Ti, the coefficients for Ti and N2, and the molar volume of a gas at STP. The factor label set up is shown below with units and no numbers. (We always recommend doing your set-up of conversion factors without numbers. Numbers can be added later.)
Observe the placement of units. In the first conversion factor, grams Ti is in the denominator to cancel the grams Ti on the given quantity; since this is a molar mass conversion factor, the moles of Ti is in the numerator. In the second conversion factor, the moles of Ti is in the denominator to cancel the moles of Ti in the numerator of the first conversion factor. Since the second conversion factor involves coefficients, the moles of N2 are in the numerator. In the third conversion factor, the moles of N2 are in the denominator to cancel the moles of N2 are in the numerator of the second conversion factor. Since the third conversion factor uses molar volume information, the numerator includes the Liters of N2. A unit in the denominator will cancel an identical unit in any numerator (or of the given quantity). All units cancel with the exception of the Liters of N2. This uncancelled unit is the unit on our answer.
Once the conversion factors are set up so as to cancel units, numbers are inserted into each numerator and denominator. Use a periodic table to determine the molar mass value. Molar mass is the mass per 1 mole; so place the 1 with mol and the 47.867 with grams. In the middle conversion factor, place the 3 with the mol Ti since the coefficient in front of Ti is 3. Place the 2 with mol N2 since the coefficient in front of N2 is 2. Finally, the molar volume at STP is 22.4 liter per 1 mole so place the 22.4 with the L and put the 1 with the mole.
Once the problem is set up, it is time to pull out your calculator. (If you pulled out your calculator before this point in time, then you pulled it out too soon.) Multiply the given quantity by all the numbers in the numerator and divide by all the numbers in the denominator: 17.8 * 1 * 2 * 22.4 / 47.867 / 3 / 1. Round your calculated answer to the proper number of significant digits and record the result.
We took our time on this example. We will go faster on the next example. But if you’re just learning or having difficulty learning, it is important that you take your time. Taking your time means that you …
- … use a sheet of paper and a writing utensil. This isn’t head math.
- … use Mole Island to plot out a strategy.
- … set up your conversion factors first without numbers, so as to cancel units.
- … insert numbers into the numerators and denominators of the conversion factors.
- … keep your calculator where it belongs (out of reach) before it is time to use it.
All of these habits have proven year after year to eventually lead to student success. On the other hand, student frustration is almost always associated with the skipping of steps 1 through 4.
If you are having trouble learning stoichiometry, then we also recommend that you take the time to review Lesson 2 of our Chapter 9.
Example 3
For the reaction
3 Ti(s) + 2 N2(g) → Ti3N4(s)
Determine the moles of Ti3N4 that will be produced from the reaction of 165 L of nitrogen at STP.
Solution:
Our Mole Island analysis is shown below. This problem will involve two conversion factors. The first will include molar volume information. The second will include coefficients.
We pull out a sheet of paper and set up our conversion factors - with units and no numbers. We do it so as to cancel units and end up with moles Ti3N4 as the uncancelled unit. This is shown below. Notice how the units cancel.
Now we substitute numerical values into the conversion factors, remembering that molar volume information goes into the first conversion factor and coefficients into the second conversion factor.
Finally, we get to use our calculator. We have all the confidence in the world that our calculation will be correct because we have already done the difficult work - setting up the solution. We multiply the given quantity (165) by all the numerator numbers and divide by all the denominator numbers. We round the answer to three significant digits.
Conclusion
The problems on this page one of two types of conditions: The solution was dependent upon the conditions of the problem. The first condition was that all reactants and products are in the gaseous state at the same temperature and pressure. We used the coefficients as volume ratios. The second condition was that at least one of the reactants or products (but not all) were present as a gas at STP. We used the molar volume of a gas at STP in the solution, combining it with the other conversion factors that are typically used in a stoichiometry problem. On the next page, we will learn how to solve gas stoichiometry problems for non-standard conditions.
Before You Leave
- Download our Study Card on Gas Stoichiometry at Standard Conditions. Save it to a safe location and use it as a review tool. (Coming Soon.)
- Problem Set GL15 in our Calculator Pad section includes six problems in which coefficients are used as volume ratios. It’s great practice! Visit Problem Set GL15: Gas Stoichiometry 1.
- Problem Set GL16 in our Calculator Pad section provides six problems involving STP conditions. More great practice! Visit Problem Set GL16: Gas Stoichiometry 2.
- The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1. The combusion of butane gas (C4H10) takes place according to the following balanced chemical equation:
2 C4H10(g) + 13 O2(g) → 8 CO2(g) + 10 H2O(g)
Determine the volume of oxygen gas that will completely react with 32.5 mL of C4H10.
2. An outdoor gas grill burns propane according to the following balanced chemical equation.
C3H8(g) + 5 O2(g) → 3 CO2(g) + 4 H2O(g)
Caclulate the volume of carbon dioxide gas produced by the burning of 12.2-L of propane. Assume that all gases are present at the same temperature and pressure.
3. The rusting of iron results in the production of iron(III) oxide (a.k.a. rust) according to the following balanced chemical equation.
4 Fe(s) + 3 O2(g) → 2 Fe2O3(s)
Determine the volume of oxygen gas at STP conditions which would be needed to completely oxidize 26.1 g of iron.
4. In a classroom demonstration, a Chemistry teacher reacts zinc with an aqueous solution of HCl to produce hydrogen gas.
Zn(s) + 2 HCl(aq) → ZnCl2(aq) + H2(g)
Calculate the volume of hydrogen gas produced from the reaction of 4.95 g of zinc at standard temperature and pressure conditions.