Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 3: Gas Stoichiometry
Part c: Gas Stoichiometry at Non-Standard Conditions
Part a: Stoichiometry Revisited
Part b: Gas Stoichiometry at Standard Conditions
Part c: Gas Stoichiometry at Non-Standard Conditions
Measuring Amounts of Gases
The standard unit for the amount of a substance is the mole. The amount (moles) of a solid or liquid present in a sample of a pure substance is determined by massing the sample. If you know the mass of a sample of copper, you can easily determine the amount of copper using the molar mass 
of copper. But the mass of a gas is not a quantity that is easy to accurately determine. The amount of a gas is determined by measurement of its volume, temperature, and pressure. Together, these three quantities allow one to determine the number of moles of a gaseous sample of matter.
If the temperature and pressure of the sample happen to be standard temperature and pressure, then the moles can be calculated from its volume using 22.4 L/mol as the molar volume. But at non-standard conditions, the moles of a substance must be calculated by using the ideal gas law equation: P•V = n•R•T. The equation can be rearranged to solve for moles: n = P•V/(R•T). For gases, the pressure, volume, and temperature provides a measure of the amount of gas in the same way that mass in grams provides a measure of the amount of a solid or liquid.
Mole Island for Gases at Non-Standard Conditions
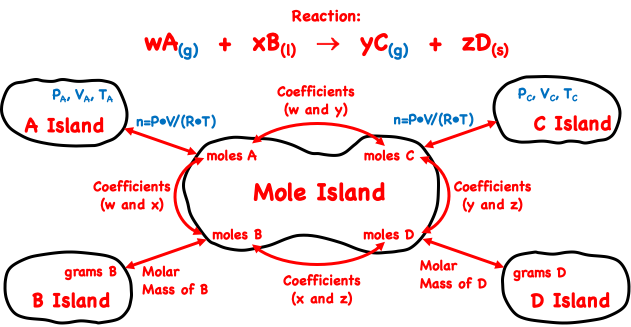
We have been referencing Mole Island throughout Lesson 3. Mole Island is a graphic organizer that allows a Chemistry student to navigate through the solution to a stoichiometry problem. It lists all the relevant How much? quantities and uses arrows to show pathways from a given quantity to a desired quantity. The graphic organizer that was first introduced in our Stoichiometry chapter is shown at the right.
As mentioned above, the amount or moles of a gas is seldom determined from its mass. Instead, the ideal gas law equation (P•V = n•R•T) is used to determine the moles of a gas from measurements of its volume (V), pressure (P), and Kelvin temperature (T). The Mole Island graphic has been revised to show the relationship between P-V-T quantities and the moles of a gaseous reactant or product. The revisions to Mole Island are shown in blue below and apply to the gaseous reactant (A) and product (C) in the equation.
Let’s discuss a generic example to illustrate how to use Mole Island to navigate your path through a stoichiometry problem. Suppose you are given the volume, temperature, and pressure of substance A (a gas) and wish to determine the mass of reactant B (a liquid) that will react with it. How would you proceed? How many conversion steps are involved and what information is used to perform the conversions?
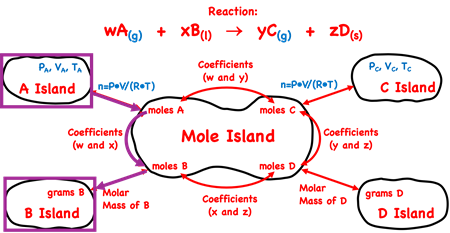
To answer such a question, begin by identifying the starting point (the given quantity) and the final destination (the desired quantity) on the diagram. This is done using purple boxes. There are three arrows between the starting point and the final destination. Thus, the problem will involve three steps. The first step is not a conversion factor step. The pressure and temperature are non-standard conditions so you are not able to use 22.4 L/mole as the pathway between volume and moles. Instead, you will use n = P•V/(R•T) to calculate the moles of substance A. Substitute known values of P, V, and T into the equation and calculate the n value. Once you know the moles of substance A (on Mole Island), there are two conversion steps. The first conversion factor involves the use of coefficients from the balanced equation. The second conversion factor will involve the molar mass of substance B.
Examples 1, 2, and 3 below model this approach.
Example 1
The rusting of iron results in the production of iron(III) oxide (a.k.a. rust) according to the following balanced chemical equation.
4 Fe(s) + 3 O2(g) → 2 Fe2O3(s)
Determine the volume of oxygen gas at a temperature of 25.2°C and a pressure of 1.05 atm that would be needed to completely oxidize 82.9 g of iron.
Solution:
We have customized our Mole Island graphic for this reaction, replacing the generic reaction with the actual reactants and products of this example problem. We have also used purple rectangles to identify the starting point (grams of Fe on Fe Island) and the final destination (volume of O2 on O2 Island).
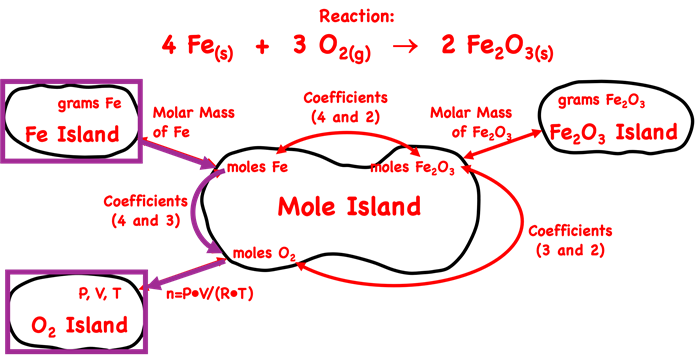
As can be seen, there are three arrows between the starting point and the final destination. This indicates that this is a three step problem. The first two steps will utilize the factor label method. The molar mass of Fe and the coefficients for Fe and O2 will be used to determine the moles of O2. The moles of O2 is n in the P•V = n•R•T equation. The pressure and the temperature are known to be 1.05 atm and 298.35 K (the given 25.2 plus 273.15). From knowledge of n, P, and T, the volume can be calculated.
The first two steps involve the use of conversion factors. The factor label set up is shown below with units and no numbers. (We always recommend doing your set-up of conversion factors without numbers. Numbers can be added later.) Observe how the units cancel. Color-coded diagonal lines show that a unit in a denominator will cancel the identical unit in the numerator of another conversion factor or in the given quantity.
Once the conversion factors are set up to cancel units, numbers can be inserted into each numerator and denominator. Use a periodic table to determine the molar mass value. Molar mass is the mass per 1 mole; so place the 1 is inserted in front of mol and the 55.845 is inserted in front of grams. In the middle conversion factor, place the 4 with mol Fe since the coefficient in front of Fe is 4. Place the 3 with mol O2 since the coefficient in front of O2 is 3.
Use your calculator to determine the moles of O2. The unrounded figure will be used in the next part of the problem.
The factor label method takes care of the first two steps of the three-step problem. The third step involves calculating V in the P•V = n•R•T equation. Rearrange the equation to solve for V:
V = n•R•T/P.
The known information is …
P = 1.05 atm
T = 25.2 + 273.15 = 298.35 K
n = 1.113349 … mol (calculated above)
Substitute and solve for V:
V = (1.113349 … mol)•(0.08206 L•atm/mol/K)•( 298.35 K) / (1.05 atm)
V = 26.0 L (rounded from 25.959705 …)
Commit to an Effective Approach
Reflecting on the above solution reveals a number of habits that will serve a Chemistry student in any problem that they approach. You will notice that we took our time. Good problem-solving can never be rushed. As you improve your skill, you will go faster but you still won’t be rushing. You always need to proceed as slow as is needed in order to …
- Get out a sheet of paper and a writing utensil. This isn’t head math and your calculator is pretty useless if you don’t have a plan. Develop your plan on paper.
- Plan a solution strategy. Use Mole Island to help plot out the strategy. How many steps are there? What information will be used in each step?
- Set up your conversion factors for the converting steps. Get the units in the right location first so that the units cancel. Save the numbers for last. Only use your calculator once you know where the numbers belong.
- A PV=n•R•T step will require that you carefully work out your algebraic manipulation and substitution. List what you know. Rearrange the equation. Substitute. Solve. The calculator is only used in the Solve part.
The critical steps are the strategizing steps. Taking the time to do them will seem like your wasting time. But the time spent strategizing is time spent learning. With practice, you will observe that your doing the strategizing more quickly and naturally. You will also observe that there is less frustration and failure.
The above example shows a systematic way to solve a stoichiometry problem that works. It takes observing lots of examples and much practice to improve your skill. We have two more examples and some practice suggestions in the Before You Leave section. For the following two examples, try to solve the problem on your own. When ready or if you get stuck, tap on the Check Answer button to view the answer and complete solution.
Example 2
Oxygen gas is produced by the thermal decomposition of potassium chlorate. Determine the volume of O2 produced at 425°C and 0.983 atm from the decomposition of 4.55 g of KClO3.
2 KClO3(s) → 2 KCl(s) + 3 O2(g)
Solution:
Example 3
In a classroom demonstration, a Chemistry teacher reacts zinc with an aqueous solution of HCl to produce hydrogen gas.
Zn(s) + 2 HCl(aq) → ZnCl2(aq) + H2(g)
Calculate the volume of hydrogen gas produced at 78.2°C and 772 mm Hg from the reaction of 12.5 g of zinc.
Solution:
Before You Leave
- Download our Study Card on Gas Stoichiometry at Non-Standard Conditions. Save it to a safe location and use it as a review tool. (Coming Soon.)
- Problem Set GL17 in our Calculator Pad section provides six problems involving STP conditions. It’s great practice! Visit Problem Set GL17: Gas Stoichiometry 3.
- The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1. In the reaction
2 KClO3(s) → 2 KCl(s) + 3 O2(g)
It is observed that 15.7 L of O2 gas are produced at 271.3°C and 1.26 atm. Determine the mass of KClO3 that decomposed.
2. What mass of iron is produced from the reaction of 44.2 L of O2 at 39.5°C and 745 mm Hg?
4 Fe(s) + 3 O2(g) → 2 Fe2O3(s)