In the previous section of this lesson, we explored how magnets can be used to steer the path of a moving charged particles.  We also saw that physicists use the direction that a charged particle bends in a B-field to determines their charge.  In this part of the lesson, we are going to see how magnets can be used to find the mass of charged particles—particles so small that placing them on a balance just won’t work.  We will explore a device called a mass spectrometer.  Scientists often use this device to determine the mass of atoms and their isotopes.

While there are various types of mass spectrometers, they all work on a similar principle.  We will explore the mass spectrometer developed by Kenneth Bainbridge in the 1930’s.  We’ll consider this device in three parts:  (1) the ionizer and linear accelerator, (2) the velocity selector, and (3) the bending magnet and detector.  Let’s explore each of these individually before putting them all together to find a particle’s mass.

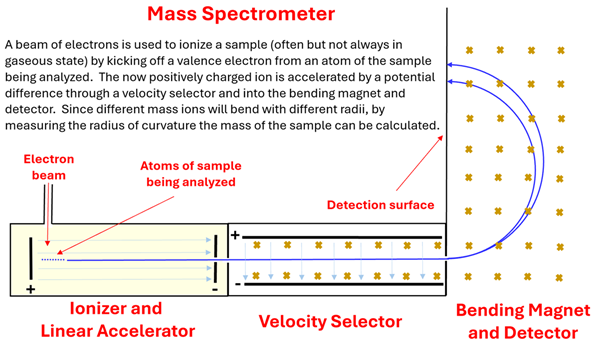
A beam of electrons is used to ionize a sample (often but not always in a gaseous state) by kicking off a valence electron from an atom of the sample being analyzed.  The now postivily charged ion is accelerated by a potential difference through a velocity selector and into the bending magnetic and detector.  Since different mass ions will bend with different radii, by measuring the radius of curvature the mass of a sample can be calculated.

Part 1: The Ionizer and Linear Accelerator

Let’s say we are scientists trying to find the mass of the elements on the periodic table and their isotopes.  How could we determine the mass of an individual atom?  We can’t, for example, just put an atom of carbon on a balance.   What we could do, however, is start with a sample of carbon atoms and, taking advantage of a process called ionization, use a beam of electrons to ‘kick-off’ an electron from each of several carbon atoms.  This gives us a bunch of positively charged carbon ions.   By having these positively charged ions start between two plates with a potential difference across them, we can accelerate them.  This part of our device is the ionizer and linear accelerator.  We learned in a former lesson that the electric field between the two plates does work on a charged particle.  This work done is equal to the kinetic energy gained.  This electric field accelerates the particles in a straight line giving them a large velocity.  At this point, we have a bunch of fast-moving, positively charged ions of carbon.

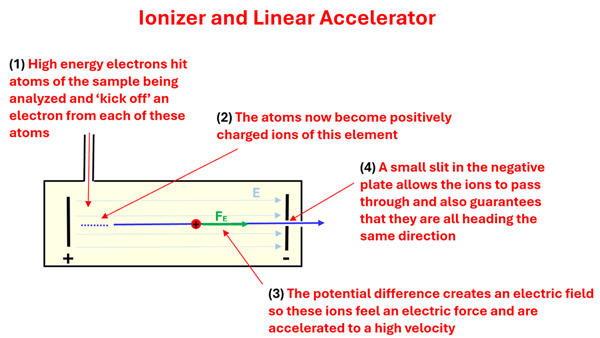
1: High energy electrons hit atoms of the sample b eing analyzed and 'kick off' an electron from each of these atoms.  2: The atoms now become positively charged ions of this element.  3: The potential difference creates an electric field so these ions feel an electric force and are accelerated to the right to a high velocity.  4: A small slit in the negative plate allows the ions to pass through and also gaurentees that they are all heading the same direction.

Part 2: The Velocity Selector

The next part of our device is the velocity selector.  While the linear accelerator gave our carbon ions a large kinetic energy, there is no guarantee that they all have exactly the same velocity.  It will be important for us to know their velocity, however, in order to determine their mass. 

The velocity selector consists of a region with both an electric field and a magnetic field that are perpendicular to each other.  In the figure shown, the electric field will exert an electric force on these ions causing them to bend downward toward the negative plate.  Using our Force-finding Right Hand Rule we can see that a magnetic field that points into the page will cause the carbon ions to feel a magnetic force upward.  The ratio of the electric field to the magnetic field selects the exact velocity desired—the velocity for which the ions will travel straight through our velocity selector undeflected.  This occurs since the electric force and the magnetic force are equal in magnitude and opposite in direction.  We can ignore the gravitation force on these ions since it will be insignificant compared to the electric and magnetic forces.

If the charged ion is moving too fast, the magnetic force will be stronger than the electric force causing the carbon ions to bend upward.  When the charged particle is moving too slow, the electric force will dominate causing the particles to bend downward.  If the ion is moving at just the right velocity (that is, at v=E/B), then it will move straight through to the final part of the mass spectrometer and will have a known velocity.      

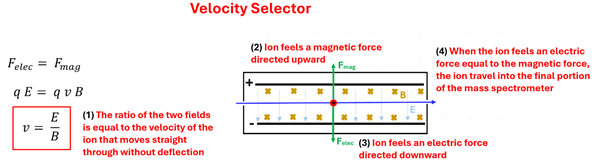
Electric Force = Magnetic Force, or q E = q v B, or v (velocity) = E over B. 1: The ratio of the two fields is equal to the velocity of the ion that moves straight through without deflection.  2: Ion feels a magnetic force directed upwards.  3: Ion feels an electric force directed downwards.  4: When the ion feels an electric force equal to the magnetic force, the ion travels into the final portion of the mass spectrometer.

Example 1: Finding an Ion's Velocity

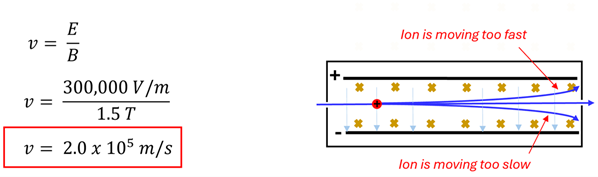
Problem:  A positively charged carbon ion enters a velocity selector with a downward pointing electric field of 300,000 V/m and a magnetic field of 1.5 T directed into the page.  What is the velocity of the ion that travels straight through undeflected?

Solution:  Using the velocity selector equation, we can determine the velocity of the singly charged carbon ion that would travel undeflected.  It is interesting to note that an ion traveling a little slower than this velocity would still feel the same electric force but would feel a smaller magnetic force.  Thus, the slower ion would bend downward and not make it to the bending magnet portion of the mass spectrometer.  An ion traveling too fast would still feel the same electric force but a larger magnetic force.  This ion would bend upward and miss the opening into the final portion of the mass spectrometer.  It is only those ions traveling at just the right velocity (2.0 x 10⁵ m/s, for this example) that will make it into the bending magnet.

Part 3: The Bending Magnetic and Detector

For the carbon ions that make it straight through the velocity selector, we now know their velocity.  This is important as they enter the final stage of our device, the bending magnet and detector.  At this stage, only a magnetic field is present and perpendicular to the ion’s velocity.  As the carbon ions enter this known magnetic field, it will feel a magnetic force that causes them to bend in a circular path as we saw in the previous section of this lesson.  This leads to a method for determining the mass of these carbon ions.

Start with Newton's Second Law, Magnetic Force = mass times accelleration.  replace acceleration with centripetal acceleration which is velocity squared over radius, and replace Magnetic Force with Particle charge times velocity times perpendicular magnetic field (q v B).  Then perform basic algebra to get mass equals the particle's charge times the perpendicular magnetic field strength times the radius over the velocity.  1: Ion now feels only a magnetic force directed towards the center of the circular path it will follow.  2: More massive ions will bend in a large radius allowing for the mass to be determined.  3: Detector surface records where ions hit.

Example 2: Determining an Ion's Mass

Problem: Singly charged positive carbon ions enter the bending magnet (B = 1.50 T) of a mass spectrometer with a speed of 2.00 x 10⁵ m/s.   Some bend with a radius of 1.66 cm and others bend with a radius of 1.80 cm.  What are the masses of the two carbon ions?  Use the previous lesson's table as needed.

Solution: Using the bending magnet’s mass equation we find the masses to be 1.99 x 10^-26 kg and 2.16 x10^-26 kg respectively.  Since the mass of one proton or neutron is approximately 1.67 x 10^-27 kg, the masses of these two ions in atomic mass units are 12 amu and 13 amu respectively.  Thus, we can identify these at Carbon-12 and Carbon-13, two isotopes of carbon.

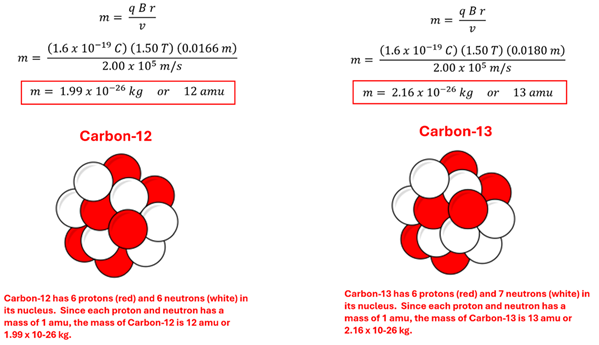
Have you ever noticed on the periodic table how the atomic mass of various elements is not a whole number even though the atom is made up of an integer number of protons and neutrons each with an atomic mass of 1 amu?  This is because atoms of that element often consist of different isotopes (that is, they have different numbers of neutrons.)  The value given on the periodic table is the weighted average of relative abundance of these isotopes.  The mass spectrometer detects these different isotopes as each one has a slightly different mass and thus bends with a slightly different radius.

Check your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.

1. The Linear Accelerator.  Select the statement that best describes the main purpose of the linear accelerator.
  A: Selects only certain velocity particles
  B: Seperates atoms into their respective masses
  C: Gives kinetic energy to ions being analyzed

2. The Velocity Selector.  A velocity selector consists of two parallel plates (as shown) with an electric field of 48 kV/m between them. A magnetic field of 0.80 T is also present.

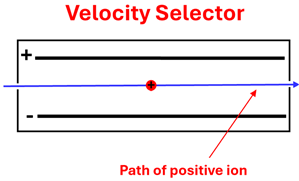
  A: What direction would you need the magnetic field to point so that a positively charged ion could pass straight through the velocity selector undeflected?
  B: What is the velocity of the undeflected ions that passed straight through?

3. The Bending Magnet.  Assume singly charged ions (q = +1.6 x 10^-19 C) enter the bending magnet (B = 0.80 T) with a velocity of 6.0 x 10⁴ m/s. 
  A: If they bend in a radius of 5.81 cm, determine the mass (in kg) of this ion.
  B: Using the below periodic table and given that 1 amu = 1.66 x 10^-27 kg, what element is probably in your sample?

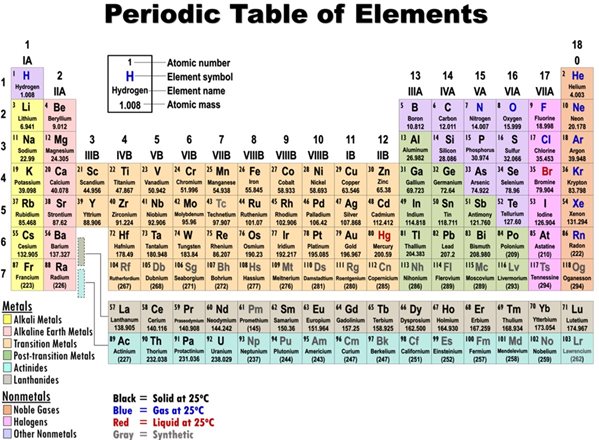
Figure 1

We Would Like to Suggest ...

Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our Mass Spectrometer and Average Atomic Mass Interactives. You can find it in the Physics Interactives section of our website.

Visit:  Mass Spectrometer and Average Atomic Mass

 
Figure 1 Source: https://commons.wikimedia.org/wiki/File:Periodic_table_of_elements.png