Chemistry: Particles <==> Moles <==> Grams

Particles-Moles-Grams: Problem Set Overview

There are 14 ready-to-use problem sets on the topic of Particles, Moles, and Grams. These problem sets focus on the use of Avogadro's number and molar mass values to convert between the number of particles in a sample, the moles in a sample, and the mass of the sample. Percent composition calculations, empirical formula determinations, and average atomic mass calculations are also included in this set of problems. Problems range in difficulty from the very easy and straight-forward to the difficult and complex. 

 

Average Atomic Mass

Each element of the Periodic Table has a unique number of protons. This number is known as the atomic number. But the number of neutrons possessed by an atom of a given element can vary from atom to atom. For instance, all atoms of carbon (C) have 6 protons. But carbon atoms exist with 6 neutrons, 7 neutrons, and 8 neutrons. Atoms of the same element that have different number of neutrons are known as isotopes. Carbon has three such isotopes; we refer to them as Carbon-12, Carbon-13, and Carbon-14. The numbers 12, 13, and 14 refer to the mass number of the three isotopes of carbon. The mass number is the sum of the atomic number (# of protons) and the number of neutrons. 

The periodic table lists the atomic masses of the various elements. The mass of a specific isotope relative to the mass of another isotope is easily determined using a mass spectrometer (but that's another topic all together). The point is that the relative atomic mass can be determined experimentally. The word relative means that we can only determine the mass of a Carbon-14 isotope relative to the mass of a carbon-12 isotope. For instance, we might determine Carbon-14 to be 1.166706 times greater than the mass of a Carbon-12 isotope. Or we might determine the mass of a Magnesium-24 isotope to be 1.998972 times greater than the mass of a Carbon-12 isotope. Or we might determine that the mass of a Phosphorus-30 isotope is 1.499392 times greater than the mass of a Neon-20 isotope. These are all made-up numbers; but you get the idea. By experiment, we can determine the mass of one atom relative to another atom ... but not the actual mass of the atom itself.

So because chemists must start somewhere when determining the actual mass, it as decided to designate Carbon-12 to have a mass of exactly 12.00000 units. This Carbon-12 isotope is the basis for the mass of all the other isotopes. The unit of mass is referred to as the atomic mass unit and abbreviated amu. The mass of all other isotopes can be determined experimentally using the assumption that Carbon-12 has a mass of exactly 12.000000 amu.

Since the mass of an atom is largely dependent upon the number of protons and neutrons, the mass of an atom of any element depends upon the mass number of the specific isotope of that element. Since a sample of an element like carbon is likely to have all three isotopes present, we commonly refer to the average atomic mass of carbon. The average atomic mass is the weighted average of the mass of the various isotopes of that element. The average atomic mass of an element with three isotopes is calculated by the equation:

Ave. Atomic Mass = ( AM₁*PA₁ + AM₂*PA₂ + AM₃*PA₃ ) / 100

where AM₁, AM₂, and AM₃  represent the atomic mass of isotopes 1, 2, and 3, and
PA₁, PA₂, and PA₃ represent the percent abundance of isotopes 1, 2, and 3.

 

Avogadro's Number and the Mole

Atomic mass values for the various isotopes allow a chemist to compare the mass of one atom relative to another atom. But atoms are very, very small and one could never isolate a single atom and measure its mass. So the concept of atomic mass and the atomic mass unit is a largely impractical concept when it comes to making a measurement. There is a need to somehow super-size this concept of an atomic mass. While one could never isolate a single atom, let alone find a scale that is sensitive enough to measure its mass, it might be possible to have some super-sizing factor so that we could mass a large collection of atoms. 

The super-sizing factor is known as Avogadro's number. Avogadro's number is a number that has come to be known as 6.022 x 10²³. When there are this number of atoms in a sample, we say there is a mole of atoms. In this sense, a mole is a counting unit much like the pair (2), the dozen (12), and the gross (144) are counting units. When the club president arrives at the Tuesday morning officer's meeting and says I have a dozen donuts, she means that she has 12 donuts. And if the hardware store owner says she has a gross of bolts, she means that she has 144 bolts. And if the chemist says that she has a mole of atoms, she means that she has 6.022 x 10²³ atoms. In this sense, the mole is defined as an amount of things equivalent to 6.022 x 10²³ things.

1.0 mole = 6.022 x 10²³

So the number 6.022 x 10²³ becomes the super-sizing factor that converts atomic mass to molar mass. If a single atom of carbon has a mass of 12.0107 amu, then 1.00 mole of carbon atoms (6.022 x 10²³ C atoms) has a mass of 12.0107 grams. And if a single atom of oxygen has a mass of 15.9994 amu, then 1.00 mole of oxygen atoms (6.022 x 10²³ O atoms) has a mass of 15.9994 grams. So the average atomic mass values listed on the Periodic Table indicate the mass in grams of 1 mole of atoms of that specific element. While the amu is the unit used to describe the mass of a single atom, grams is the unit used to describe the mass of a mole of atoms. We refer to the mass of 1.00 mole of atoms as the molar mass. Molar mass values have units of grams/mole.


 

Molar Mass

The Periodic Table lists the molar masses of the various elements. These values, listed in units of grams/mole (g/mol) provide a quantitative measure of the mass of 6.022 x 10²³ atoms of a typical sample of that element. For example, a typical sample of carbon atoms consisting of the typical mix of its isotopes and consisting of 6.022 x 10²³ atoms would have a mass of 12.0107 grams. And a typical sample of aluminum atoms that consisted of 6.022 x 10²³ atoms of the typical mix of aluminum isotopes would have a mass of 26.9815 grams. In this sense, the molar mass values indicate the mass per mole of atoms of each element. 

But what about a compound? How does one go about determining the molar mass of a compound that consists of more than element? A molecule of a compound consists of a collection of atoms. For water (H₂O), a molecule consists of two H atoms and one O atom. And for the compound P₂O₅, a single molecule would consist of two P atoms and five O atoms. And for the compound H₂SO₄, a single molecule would consist of two H atoms, one S atom, and four O atoms. So finding the molar mass of a compound - the mass of 1 mole of it's molecules - can be done by summing the mass for a mole of each of its elements.

For water (H₂O), this means summing the mass of two moles of H atoms and one mole of O atoms:
Molar Mass of H₂O = 2*(1.0079 g/mol) + 1*(15.9994 g/mol) = 18.0152 g/mol

And for P₂O₅, the molar mass is the sum of the the mass of two moles of P atoms and five moles of O atoms:
Molar Mass of P₂O₅ = 2*(30.9738 g/mol) + 5*(15.9994 g/mol) = 141.9446 g/mol

And for H₂SO₄, the molar mass is the sum of the the mass of two moles of H atoms, one mole of P atoms, and four moles of O atoms:
Molar Mass of H₂SO₄ = 2*(1.0079 g/mol) + 1*(32.065 g/mol) + 4*(15.9994 g/mol) = 98.0789 g/mol

 

 

Particle-Mole-Gram Conversions

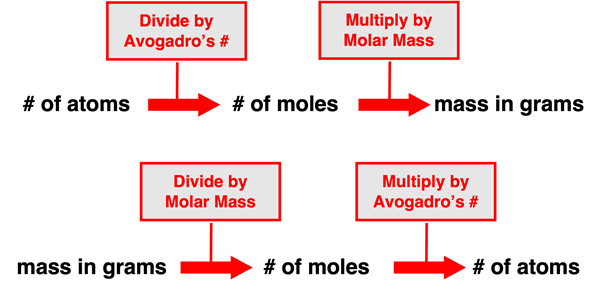
The number of particles (atoms or molecules) in a sample of a substance (element or compound) is related to the number of moles of that substance. Avogadro's number tells us how many items are in a mole of items. Since 1 mole of particles = 6.022 x 10²³ particles, Avogadro's number is used when converting between the number of particles and the number of moles. Converting from the number of moles to the number of particles involves multiplying by Avogadro's number. And converting from the number of particles to the number of moles involves dividing by Avogadro's number. We can think of such conversions as involving a single step of multiplication or division.

The mass of a sample of a substance (element or compound) is related to the number of moles of that substance within the sample. The molar mass of a substance describes the mass in grams of one mole of that substance. So when we say the substance carbon dioxide (CO₂) has a molar mass of 44.01 g/mol, we mean that a mole of that substance's particles would have 44.01 grams of mass. And so the molar mass becomes a means of converting between the grams of a substance and the number of moles of a substance. Converting the mass of a substance in grams to the number of moles involves dividing by the molar mass. And converting the number of moles of a substance to the mass in grams involves multiplying by the molar mass. Once more we can think of such conversions as involving a single step of multiplication or division.

We can put the ideas of these two paragraphs together to reason how the number of particles of a substance is related to the mass of that substance in grams. The conversion of the number of particles to the mass in grams would involve two steps. First one must divide by Avogadro's number and then multiply by the molar mass. The first of these two steps converts particles to moles and the second step converts the moles to the mass in grams. The conversion of the mass in grams to the number of particles also involves two steps. First one must divide the mass by the molar mass and then multiply by Avogadro's number. The first of these two steps converts the grams to moles and the second step converts the moles to the number of particles. The graphic below summarizes these conversions.

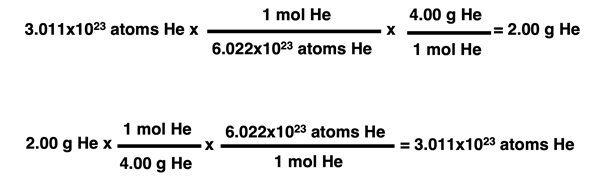
It is the tendency of chemistry students to read these paragraphs and begin memorizing the steps for the various conversions. But in Chemistry, there is usually a much better alternative to memorizing. That alternative often involves the use of conversion factors and unit cancellation. This method, sometimes referred to as the factor-label method, was discussed in a different unit of the Calculator Pad. Conversion factors can be used to convert between grams and moles and between moles and the number of particles and even in the reverse direction. It is recommended that you review the factor-label method if you are a bit rusty on it. The graphic below demonstrates the use of conversion factors to perform the two-step conversions between the number of particles and the mass in grams. Study the graphic below and compare it to the multiplication and division operations described in the graphic above.

 

Determining the % Composition from the Formula

A chemical formula for a compound uses subscripts to indicate the relative ratio of atoms of each element in a molecule of that compound. So for the simple case of H₂O, the formula indicates that there are 2 atoms of hydrogen per every one atom of oxygen. And if we super-size our thinking about the H₂O formula to the level of moles, we would reason that there are two moles of H atoms per every one mole of O atoms in a mole of H₂O molecules. And using the molar masses of the two elements in water ...
H: 1.0079 g/mol
O: 15.9994 g/mol
... we would reason that there are 2*1.0079 grams of H per every 15.9994 grams of O. So if we had a mole of water molecules having a mass of 18.0174 grams, then we coulduse this information to determine what percentage by mass of water is hydrogen and what percentage by mass is oxygen. Here's the calculations:

%H = (2*1.0079 g)/(18.0174 g) * 100 = 11.20%
%O = (15.9994 g)/(18.0174 g) * 100 = 88.80%

Note that the calculation of the percentage of an element is the mass of that element in one mole of the compound divided by the mass of one mole of the compound multiplied by 100. 

 

Molecular vs. Empirical Formula

The molecular formula of a substance indicates the number of atoms of each element that are actually present in one molecule of that substance. The substance benzene has a molecular formula of C₆H₆. One molecule of benzene has six atoms of carbon and six atoms of hydrogen within in it. The empirical formula of a substance describes the simplest ratio of the atoms of each element in the compound. So using benzene as our example, the empirical formula is CH. As a second example, the compound ethylene has a molecular formula of C₂H₄ but an empirical formula of CH₂.

 

 

Determining the Empirical Formula from the % Composition

Chemical analysis of an unknown substance allows chemists to determine the percent composition of the elements within the substance. This percent composition data can in turn be used to determine the empirical formula of the substance. As an example, suppose that an unknown substance is determined to consist of only hydrogen and oxygen and determined to be 5.93% hydrogen and 94.07% oxygen by mass. With this being the case, you would reason that a 100.00-gram sample of the substance would consist of 5.93 g of H and 94.07 g of O. Since we know the molar masses of the elements H and O, we can convert the masses of each element to the number of moles. It goes like this:

# moles of H = 5.93 g*( 1.00 mol/1.0079 g) = 5.88 mol of H
# moles of O = 94.07 g*( 1.00 mol/15.9994 g) = 5.88 mol of O

From our calculations we conclude that a 100.00-gram sample contains an equal number of moles of H and O. And since the empirical formula indicates the simplest ratio of atoms of the elements in a compound, then we would reason that this unknown substance has an empirical formula of HO. One possible identity of our substance is hydrogen peroxide, whose molecular formula is H₂O₂.

A useful method for determining the empirical formula from % composition data involves the following sequence of steps:

1. Assume a certain mass of the substance. Assuming a 100.00-gram sample is a great starting point (a bit better than 117.38 grams).
2. Determine the mass of each element in the sample of the assumed mass (from step 1).
3. Use molar mass values to calculate the moles of each element in this assumed mass of substance.
4. Scan the mole amounts calculated in step 3. Divide each mole amount by the lowest number of moles. This gives the ratio of the  relative number of moles of each element in the compound. If the results are whole numbers or close enough to whole numbers to round them, you can write the empirical formula from the results. If not ...
5. Choose a multiplying factor like 2 or 3 or 4 to scale each relative number of moles to a whole number. Use the same multiplying factor for each element. With the relative mole amounts now being whole numbers, write the empirical formula.

 

Habits of an Effective Problem-Solver

An effective problem solver by habit approaches a chemistry problem in a manner that reflects a collection of disciplined habits. While not every effective problem solver employs the same approach, they all have habits which they share in common. These habits are described briefly here. An effective problem-solver...

• ...reads the problem carefully and develops a mental picture of the situation. If needed, they sketch a simple diagram of the situation to help visualize it.
• ...identifies the known and unknown information and records them in an organized manner, often times equating given values to the symbols used to represent the corresponding quantity - e.g., m = 25.2; V = 16.3 mL; d = ???.
• ...plots a strategy for solving for the unknown quantity; the strategy will typically center around the use of equations or conversion factors and be heavily dependent upon an understanding of chemistry principles.
• ...identifies the appropriate formula(s) or converting factor(s) to use, often times writing them down. 
• ...performs substitutions and algebraic manipulations or strings together a series of conversion factors using the factor label method in order to solve for the unknown quantity.