Chemistry: Units and Measurement
Units and Measurement: Problem Set Overview
There are 6 ready-to-use problem sets on the topic of Refraction and Lenses. The problems focus on precision of measurement (significant digits), unit conversions, and the mass-volume-density relationship. The problem sets were designed for the early units of a Chemistry course. Problems range in difficulty from the very easy and straight-forward to the very difficult and complex.
Significant Digits and Precision
Measured quantities in Chemistry have at least three components - an amount, a unit used to express the amount, and a level of precision with which that amount is known. To illustrate, suppose the length of a pencil is measured by Student A and the measured value is expressed as 8 cm. And suppose Student B measures the length of the same pencil and determines its length to be 8.15 cm. What is the difference in the two measurements? Many people would quickly state the amount. But that's not the case. The difference has to do with the level of precision with which the measurement is made. One person (perhaps carelessly) expressed the length to the ones place. The other person expressed the length to the hundredths place. These two measurements could be compared with the words rough versus precise. They could also be compared by stating that Students' A measurement was expressed with 1 significant digit and Student B's measurement was expressed with 3 significant digits. The number of significant digits in a measurement is an indicator of how precisely known the measured value is.
There are rules for expressing the number of significant digits in a measurement. All non-zero digits in a measurement are considered significant digits. Thus, the rules for significant digits all pertain to the judging whether or not a 0 is considered significant or not. Here are the three rules:
- All leading zeroes are never significant. The zeroes in the following numbers are leading zeroes and not considered when counting the number of significant digits in a number: 0.245 and 0.00245.
- All captive zeroes are always significant. A captive zero is a zero that is surrounded by non-zero digits. The zeroes in the following numbers are captive zeroes and count towards the total number of significant digits: 2045, 20405, and 20045.
- Trailing zeroes are significant only if there is a decimal point in the number. Trailing zeroes are zeroes that come at the end of a number. The zeroes in 2.450, 2.4500, and 2450.00 are all significant digits. But the zeroes in 2450 and 24500 are not significant.
Quantities and Units
The physical sciences - chemistry and physics - are very quantitative sciences. There are quantities that are used to describe the worlds of chemistry and physics. Quantities that you might be used to are length and time. When we discuss how long the room is when can discuss as being "really long" or "actually, not very long". But we can also express it numerically. That is, we can measure the length of the room and say that it has a length of 9.28 m. Similarly, we can say that it took 56.8 seconds to walk from Chemistry class to the bathroom down the hall. Length and time are examples of measurable quantities. Other examples include mass, volume, and pressure.
The metric system is used when making measurements of these quantities. The metric system is a decimal-based system (as opposed to a fractional system). We measure a volume to be 0.50 L or 0.62 L, but never ½ L or ¾ L. Each type of quantity has its own metric unit. Examples include:
- Length: meter (m)
- Time: second (s)
- Mass: gram (g)
- Volume: Liter (L)
- Pressure: atmosphere (atm)
Of the five quantities listed, pressure is perhaps the most unique. There are numerous other units that are used to express the quantity pressure. Most have arisen due to historical reasons. Examples include mm of Hg, torr, and pounds per square inch.
Metric System and Greek Prefixes
Greek prefixes are often used in front of these units to modify the size of the unit. Consider the meter, the millimeter, and the kilometer. The prefixes milli- and kilo- are used to modify the meter. A meter is approximately 39 inches (a bit more than three feet). A millimeter is a very small length and a kilometer is a relatively large length. The prefix milli- means one-thousandth (1/1000); and so a millimeter is one-thousandth of a meter. And the prefix kilo- means thousand; so a kilometer is equivalent to 1000 meters.
Here is a list of the most commonly used Greek prefixes and their meaning.
| Prefix |
Symbol |
Meaning |
Example |
| nano- |
n |
1/1000000000-th |
109 nm = 1 m |
| micro- |
µ |
1/1000000-th |
106 µm = 1 m |
| milli- |
m |
1/1000-th |
103 mm = 1 m |
| centi- |
c |
1/100-th |
102 cm = 1 m |
| kilo- |
k |
1000 |
1 km = 1000 m |
| Mega- |
M |
100000 |
1 Mm = 1000000 m |
Because the metric system is a decimal-based system, converting from one metric unit to another metric unit involves the movement of the decimal point a certain number of places. An understanding of the above table and the meaning of the Greek prefixes is critical to understanding how many decimal places the decimal point must be moved when converting between units.
Unit Conversions and Conversion Factors
A common task in a Chemistry course is the conversion of a quantity expressed in one set of units to a quantity in a different set of units. Most chemistry courses will emphasize a conversion method known as the Factor Label Method. Because the Factor Label Method utilizes multiplying factors known as converting factors or a conversion factor, it is sometimes referred to as the Conversion Factor Method.
To illustrate the method, let's use it to do a rather simple conversion of the quantity 30.0 inches to the unit feet. Most of us are aware that there are 12 inches in 1 foot. That is,
12.0 in = 1.00 ft
The above statement is known as a unit equivalency. It relates the size of one unit (inches) to another unit (feet). Any unit equivalency can be made into a converting factor. So the above unit equivalence statement can be expressed in one of the following two ways

If we wish to convert the quantity 30.0 inches to the unit feet, we would multiply 30.0 inches by the fraction (conversion factor) on the right.

Doing so would cancel the unit inches and leave the unit feet as the uncancelled unit. The result or answer is 2.50 ft. You can convince yourself that the unit inches cancels if you remove the numbers from the above line and rewrite the line. Any unit in the numerator (upstairs) will cancel any identical unit showing up in the denominator of a conversion factor.

To gain a grasp of the Factor Label Method, you MUST give attention to units. After all the method is all about units. It's a unit-cancellation method used to convert from a quantity in one set of units to another set of units. The units are primary; the numbers are secondary.
As you become comfortable with the use of conversion factors (and in many courses, you will need to be comfortable with the use of conversion factors), you will find that you can easily string two and more conversion factors together to perform complex unit conversions. You'll need to remember that any unit equivalency can be transformed into one of two different converting factors. And a converting factor can be used in a unit cancellation procedure to convert in stepwise fashion one unit to another unit. To demonstrate, observe how 30.0 inches is converted to miles (mi) using the two unit equivalencies ...
12.0 in = 1.00 ft
5280 ft = 1.00 mi
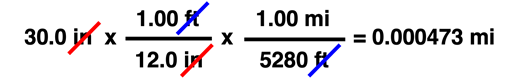
In many Chemistry courses, the Factor Label Method is not a "Unit 1 topic and drop it." Rather, it's a course-long tool used in multiple units to solve problems. In such courses, you're guaranteed that it's not going to "go away." And when that's the case, wise students will learn the method early so as to avoid the aggravation that comes with feeling like you can never solve chemistry problems.
Temperature Scales
Temperature is a quantity that is commonly used in a Chemistry course. There are numerous temperature scales used to express the quantity temperature. The two more commonly used temperature scales in a Chemistry course are the Celsius scale and the Kelvin scale. The units for these two scales are degrees Celsius (abbreviated °C) and Kelvin (abbreviated K). The size of a degree Celsius unit is equivalent to the size of a Kelvin unit. The difference between the two scales is how they define the zero temperature. In the Celsius scale, the zero temperature is defined as the temperature at which water freezes under standard pressure conditions. The temperature at which water boils at standard pressure conditions is the 100.0°C mark. So a degree unit on the Celsius scale is one-hundredth of the difference in temperature between water's freezing and boiling points. The Kelvin scale defines zero temperature as being absolute zero - the lowest temperature that can be obtained This temperature is -273.15°C. So the equation relating the temperature on the Celsius scale to the temperature on the Kelvin scale is ...
°C = K - 273.15
or
K = °C + 273.15
Since there are temperatures lower than the freezing point of water, it is possible to have negative temperature values on the Celsius scale. However, 0 K is the coldest temperature there is. There will never be a negative temperature value on the Kelvin scale. Finally, it's worth noting that since the size of a °C unit is equal to the size of a K unit, the temperature difference between the freezing point of water and the boiling point of water is 100 units on both temperature scales.
Density
Density is one of several physical properties of an object. A physically dense object has a relatively lot of stuff (mass) packed into a relatively small amount of space (volume). Density is a property that can be expressed quantitatively. The equation for density is
Density = mass/volume
d = m/V
The second line is the symbolic representation of this relationship. The d represents density, the m represents the mass, and the V represents the volume. A variety of units can be used to express the density. Each is a mass unit divided by a volume unit. Typical expressions are grams/milliliter (abbreviated g/mL) and grams/cubic centimeter (abbreviated g/cm3).
Problems involving density calculations will typically have you solving for density, mass, or volume. Like any equation in math or science, it can be rearranged to solve for any quantity that is desired. The main idea is that one must know two of the three quantities in order to solve for the third quantity in the equation. If needing to solve for the mass, the equation can be rearranged by multiplying both sides of the equation by V. This would cancel the V in the denominator of the right side of the equation, thus isolating the mass variable by itself. The equation becomes ...
m = d•V
Similarly, the d = m/V equation can be rearranged so as to isolate the variable V by itself. Deriving the V = ... equation is a bit more complicated and involves two steps of algebra. The first step involves removing the V from the denominator on the right side of the equation by multiplying both sides of the equation by V. This turns the equation into d•V = m. The second step of algebra involves dividing both sides of the equation by d in order to isolate V on the left side of the equation. The equation then becomes ...
V = m/d
Now you have three different equations for the same relationship. The equation that you use is dependent upon the quantity that you are trying to solve for.
Habits of an Effective Problem-Solver
An effective problem solver by habit approaches a chemistry problem in a manner that reflects a collection of disciplined habits. While not every effective problem solver employs the same approach, they all have habits which they share in common. These habits are described briefly here. An effective problem-solver...
- ...reads the problem carefully and develops a mental picture of the situation. If needed, they sketch a simple diagram of the situation to help visualize it.
- ...identifies the known and unknown information and records them in an organized manner, often times equating given values to the symbols used to represent the corresponding quantity - e.g., m = 25.2; V = 16.3 mL; d = ???.
- ...plots a strategy for solving for the unknown quantity; the strategy will typically center around the use of equations or conversion factors and be heavily dependent upon an understanding of chemistry principles.
- ...identifies the appropriate formula(s) or converting factor(s) to use, often times writing them down.
- ...performs substitutions and algebraic manipulations or strings together a series of conversion factors using the factor label method in order to solve for the unknown quantity.