Chemistry: Molarity and Solutions
Molarity and Solutions: Problem Set Overview
We have 14 ready-to-use problem sets on the topic of Molarity and Solutions. These problem sets focus on the use of the concept of concentration (most specifically molarity) in the analysis of situations involving solution formation, dilution, and solution stoichiometry. Problems will range from the very easy plug-and-chug to the more difficult analysis of reactions involving solutions.
Solution, Solute, Solvent
A solution is a homogeneous mixture of two or more substances. In describing it as homogeneous, we mean that the composition of the two or more substances is uniform or the same throughout the bulk of the solution. In this unit, most solutions will be aqueous solutions. In an aqueous solution, a substance is dissolved in water. We refer to water as the solvent and the substance that is dissolved in it is referred to as the solute. In most instances, the solute will be a solid that is dissolved into the water to form the aqueous solution. The dissolved solid is uniformly distributed throughout the bulk of the water, making the aqueous solution a homogeneous mixture.
Solubility Curves
Not all solids dissolve in equal amounts in water. You may have noticed that a tablespoon of table salt (NaCl) easily dissolves in a cup of water. After a little stirring, the table salt is dissolved and distributed uniformly throughout the water. A second and even a third tablespoon can often be dissolved in the same cup with little difficulty. On the other hand, a tablespoon of sucrose or granulated sugar (C
12H
22O
11) would not readily dissolve in the same cup of water. After stirring, you might noticed some undissolved crystals of sucrose at the bottom of the glass. If you were lucky enough to dissolve the first tablespoon of sucrose, it would be unlikely that a second and a third tablespoon could be dissolved in the same way that the table salt dissolved. This illustrates that not all solids dissolve in equal amounts in water.
When a solid solute is dissolved in water, the water eventually becomes saturated with the solute. The water can no longer hold more dissolved solute particles in the solution. Adding additional solute will result in undissolved solid accumulating at the bottom of the container. We say that the solution is
saturated. A saturated solution contains the maximum amount of solute that the solvent can hold at that specific temperature. The
solubility of a solute is a quantity that describes the maximum amount of solute that can be dissolved in a specific amount of solvent. For an aqueous solution, this quantity is usually expressed in units of
grams of solute per 100.0 grams of water.
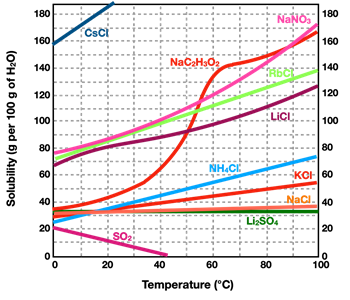
As mentioned, not all solids dissolve in equal amounts in water. In other words, different solids have a different solubility. Solubility also depends upon temperature. For most solid solutes, an increase in temperature results in an increase in the solubility of that solid solute. Put another way, more solid can be dissolved in hot water than in cold water. For some solid solutes, the effect of temperature upon the solubility is quite dramatic. For other solids, increases in temperature has a rather small effect upon the solubility. A
Solubility Curve is a graph showing the solubility of a solute as a function of temperature. The graph at the right shows the solubility curve for several solutes in water. Each line is labeled with a chemical formula to denote the solid solute that it refers to. Note that the units for solubility (along the vertical axis) are grams of solute per 100 grams of water. And note that the temperature units are °C. In nearly all instances, the lines on the graph show a noticeably positive slope. This agrees with the general trend that increasing the temperature will increase the solubility of a solid solute. The one line on the graph that shows a negative slope is the pink line in the bottom left of the graph. This is the solubility curve for SO
2 - a gas. For gases, the solubility in water shows a different pattern as for solids; increasing temperatures result in decreasing solubility of the gas.
By using axis values on a solubility curve, one can determine the solubility of the various solids at a specific temperature. Bear in mind that the solubility refers to the maximum amount of solid that can be dissolved in 100 grams of water at that particular temperature. It describes the amount of solute that can be dissolved to form a
saturated solution. One can always add less solid than the saturation amount. In such a case, the solution would be described as an
unsaturated solution. In saying that it is unsaturated, we mean that you could continue to add more solid and dissolve it in the aqueous solution.
Consider the solute NH
4Cl (the light blue line). At a temperature of 90°C, its solubility is 70.0 grams per 100.0 grams of water. At this temperature,100.0 grams of water could
hold as much as 70.0 grams of NH
4Cl. If 30.0 grams of NH
4Cl is added to 100.0 grams of water at this temperature, the solution would be unsaturated. An additional 40.0 grams of NH
4Cl could be added to the 30.0 grams of NH
4Cl that is already dissolved in the solution. If that were to occur, then the solution would become saturated (filled up) with the NH
4Cl solute.
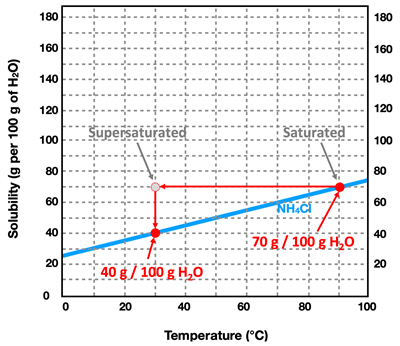
Now suppose that the saturated solution of NH
4Cl at 90°C is slowly cooled down to 30.0°C. From the curve for NH
4Cl, we notice that the solubility decreases to a value of 40.0 grams per 100.0 grams of water. That is to say, 100.0 grams of water holds 30.0 grams less solute at 30.0°C compared to 90.0°C. And so a saturated solution that is cooled down from 90°C to 30°C is overly-saturated. We use the phrase
supersaturated to describe such a solution. The 100.0 grams of water is holding more solute than it actually is able to hold. It would be analogous to me putting on a shirt at age10-years old and not taking it off for the next five years. As I grow, the shirt gets filled out (saturated) and then a year later super-saturated. Eventually that shirt is going to burst at its seams. Admittedly, that's a bit of an odd analogy ... but the idea is that as the solution is cooled down, it is eventually going to have to release some solid. It's going to burst at the seams and the 30.0 grams of extra solid is going to be released out of the solution and appear as undissolved solid. Supersaturated solutions are unstable solutions and will readily revert back to saturated solutions by allowing the additional solid to precipitate inside the container. The only way to produce a supersaturated solution is to saturate the water at a high temperature and then to slowly allow the solution to cool down to a lower temperature where the solubility is less.
Concentration: Mass Percent
The concentration of an aqueous solution describes how much solute is dissolved in a certain amount of the solution. There are a variety of ways to describe the concentration. One of those ways is the mass percent. Mass percent composition describes the mass of solute (in grams) per mass (in grams) of solution on a percent basis. The equation is ...
% Solute = ( grams of solute / grams of solution ) * 100.0
Suppose that 10.0 grams of NaCl are dissolved in 100.0 grams of water. The total mass of the solution would be the mass of the solute (NaCl, 10.0 g) plus the mass of the solvent (H2O, 100.0 g). The solution would have a mass of 110.0 grams. The mass percent of NaCl in the aqueous solution would be ...
% NaCl = ( 10.0 g / 110.0 g ) * 100
% NaCl = 9.09% (by mass)
Concentration: Molarity
Another means of expressing the concentration of solute within a solution is to use the concept of molarity. Molarity describes the concentration in terms of the number of moles of solute per liter of solution. In equation form, we would write ...
Molarity of Solute = moles of solute / Liters of solution
If one knows the moles of solute and the volume of the solution, then one can easily calculate the molarity.
Suppose that 2.00 moles of NaCl are dissolved in 0.500 liter of water. Such a solution would have a molarity of ...
Molarity = 2.00 moles NaCl / 0.500 L of water
Molarity of NaCl = 4.00 moles/liter
Note that the unit on molarity is moles/liter. Its one quantity - moles - divided by another quantity - liters. Molarity, like density, is a ratio of two quantities. As such, when a solution like this one is said to be concentrated with solute at an amount of 4.00 moles/liter, it doesn't mean that the solution has a volume of 1.0 liter. It simply means that the ratio of moles (of solute) per volume of solution (in liters) is 4:1. The larger this ratio is, the more concentrated that the solution is with solute. So a moles per liter ratio of 8:1 (8.00 moles/liter) is two times more concentrated than the 4.00 moles/liter solution.
Saying or writing moles per liter all the time can get tiring. Fortunately, the chemistry world has found a couple of abbreviated means of saying or writing it. The unit moles/liter is sometimes abbreviated as molar. A solution with a solute concentraton of 4.00 moles/liter is said to be a 4.00 molar solution. As a concentration unit, molar means moles/liter. That was better wasn't it? But we can do better still because we have a way to abbreviate the unit molar. We abbreviate the unit my replacing molar with M. A solution with a concentration of 4.00 moles per liter is a 4.00 molar solution or simply a 4.00 M solution. That is, ...
4.00 moles/liter = 4.00 molar = 4.00 M
As always in Chemistry (like many realms of study), details matter and the unit M for molar or moles/liter is a capital M. No chemist worth their salt would ever describe a solution as having an NaCl concentration of 4.00 m if they mean that there are 4.00 moles of NaCl per every Liter of solution. Details matter. Use the capital M.
Time to learn another trick. It can get quite tiring to say or write the molarity of NaCl or the molarity of NaOH. Fortunately, the chemistry world has found another short hand means of saying this. It involves enclosing the solute's chemical formula in brackets. If you see [NaCl], you can translate it to mean the molarity of NaCl. So the notation ...
[NaCl] = 0.500 M
... is describing an aqueous solution that is concentrated with the solute NaCl in an amount of 0.500 moles per every one liter of solution.
Relating Mass, Moles, Volume, and Molarity
The formula for the molarity is
Molarity of Solute = moles of solute / Liters of solution
The numerator - number of moles of solute - is related to the mass of solute. And often times, the moles of solute must be calculated from the given mass of solute. As discussed and practiced in an earlier unit, mass and moles are related by the molar mass. If the formula of the solute is known, then the Periodic Table can be used to determine the molar mass. The molar mass has units of grams/mole. It can be used to determine the number of moles of solute from the mass of the solute. Return to the earlier unit for more detailed instructions on how to convert between mass and moles. Once you have determined the number of moles of solute, you can divide by the volume of the solution to determine the molarity.
Ions and Ion Concentrations
When an ionic solid is dissolved in water to form an aqueous solution, the solid is known to dissociate. Dissociation, whether in the business world or the chemical world, is the act of splitting apart. The particles of the ionic solid split apart into their two ions. There will be a positive ion and a negative ion formed as the result of the dissociation. From an understanding of the charges of the ions and the formula of the ionic solid, one can write a chemical equation for the dissociation process. A few such equations are shown here:
NaCl(s) → Na+(aq) + Cl-(aq)
BaCl2(s) → Ba2+(aq) + 2 Cl-(aq)
AlCl3(s) → Al3+(aq) + 3 Cl-(aq)
Na2SO4(s) → 2 Na+(aq) + SO42-(aq)
Ca3(PO4)2(s) → 3 Ca2+(aq) + 2 PO43-(aq)
As you can see, the number of ions fromed by the dissociation process depends upon the number of ions present in the formula of the ionic solid. The implication of this is that the concentraion of the ions will not necessarily be equal to the concentration of the solid. Consider the dissociation of BaCl
2 as an example. If an aqueous solution of 1.5 M BaCl
2 is formed, then the barium ion concentration will be 1.5 M and the chloride ion concentration will be 3.0 M. These concentration values - 1.5 M, 1.5 M, and 3.0 M are consistent with the coefficients in the BaCl
2 dissociation equation - 1, 1, and 2. Similarly, if an aqueous solution of 0.50 M AlCl
3 solution is formed, then the aluminum concentration will be 0.50 M and the chloride ion concentration would be 1.50 M. These concentration values - 0.50 M, 0.50 M, and 1.50 M are consistent with the coefficients in the AlCl
3 dissociation equation - 1, 1, and 3. And finally, if an aqueous solution of 1.0 M Ca
3(PO
4)
2 is formed, then the calcium ion concentration will be 3.0 M and the phosphate ion concentration will be 2.0 M. These concentration values - 1.0 M, 3.0 M, and 2.0 M are consistent with the coefficients in the Ca
3(PO
4)
2 dissociation equation - 1, 3, and 2.
If you can write the chemical formula for the ionic solute, then you can write the balanced chemical equation for its dissociation. And then you can use the coefficients of that equation to determine the ion concentrations from a given value of the solute's concentration. Much of this is likely a review and applicatoin of ideas learned in previous units.
Dilution Problems
Dilution is the act of making something weaker. In chemistry, dilution involves adding additional solvent to a solution so that the concentration of the solute becomes weaker. It is a means of making the solute less concentrated. Consider 1.00 liter of a 2.00 M aqueous solution of NaCl. Such a solution consists of 2.00 moles of solute (NaCl) dissolved in 1.00 liter of water. Such a solution would become diluted if more water were added to it. Water is the solvent; adding water increases the volume of the solution without changing the amount of solute that is dissolved in the solution. So if an additional 4.00 L of water were added to the solution, thene there would be a total volume of 5.00 L. But the solution would still contain 2.00 moles of NaCl. The new molarity after dilution would be ...
[NaCl] = 2.00 mol NaCl / 5.00 L solutoin
[NaCl] = 0.40 M
There are a couple of mathematical patterns evident in this example. First, the volume of solution was increased by a factor of five - from 1.0 L to 5.0 L. This five-fold increase in the volume is accompanied by a decrease in the molarity of solute by a factor of one-fifth. Put another way, as the volume becomes five times greater, the solute concentration becomes five times smaller. The second mathematical pattern is that the product of the initial volume and the molarity is the same as the product of the final volume and molarity. In equation form,
Vinitial • Minitial = Vfinal • Mfinal
When the volume and molarity values are substituted into the equation, you can become convinced of the pattern:
(1.00 L) • (2.00 M) = (5.00 L) • (0.40 M)
2.00 L•M = 2.00 L•M
This second pattern makes sense because the
volume • molarity is equal to the number of moles. And as mentioned, dilution involves adding solute to change the volume of the solution without changing the number of moles of solute. As the calculation and discussion above shows, the number of moles of solute initially present was 2.0 moles; and that is equal to the number of moles that were present in the final solution after the dilution process occurred.
Solution Stoichiometry
Stoichiometry is the study of the quantitative relationships or ratios between substances involved in a chemical reaction. The topic was discussed and practiced with great detail in an earlier CalcPad unit. The practice of stoichiometry combines a balanced chemical equation with the use of conversion factors (the factor label method) to use the given amount of reactants and/or products in order to determine an unknown amount of reactant and/or product.
The balanced chemical equation is basis for stoichiometry. The coefficients of the balanced chemical equation identifiy the ratios by which the particles of reactants and products are involved. The coefficients in the balanced chemical equation provide the mole ratios - the ratio of moles of a reactant to the moles of a product (or other reactant). In the previous CalcPad unit pertaining to Stoichiometry, the given values in the problem were typically provided as mass values (in grams). The molar mass of the reactant (or product) was used to make a conversion factor that allowed one to convert between grams and moles. A typical three-step stoichiometry problem (a mass-to-mass problem) will utilize three conversion factors - two based on molar mass values and one based on the coefficients in the balanced chemical equation.
In this unit of the CalcPad, we will practice solution stoichiometry. A solution stoichiometry problem typically does not express the amount of reactant and product in terms of mass. Since the reactant is often an aqueous solution, the volume and the molarity of the reactant is often given. Multiplying volume • molarity yields the moles of solute for the reactant that is an aqueous solution. Suppose a reaction involves a silver nitrate solution - AgNO3(aq). And suppose a stoichiometry problem provides the amount of AgNO3 in terms of volume and molarity. For instance, it might indicate in the problem that 12.8 mL of 0.500 M AgNO3 reacted. How would this information be incorporated into the factor-label-method approach to the solution? The converting factors below show how the problem solution would be started.

Once the volume and molarity are used to determine the moles of reactant present, the solution would continue in the usual manner with a mole ratio and a molar mass being used to create the subsequent conversion factors.