Lesson 2: Chemistry as a Quantitative Science

Part a: Scientific Notation

Part 2a: Scientific Notation
Part 2b: Units and the Metric System
Part 2c: Quantities and Their Meaning


 

What is a Quantitative Science?

In Lesson 1, we learned that Chemistry is a laboratory science. Chemists (and Chemistry students) conduct lab investigations and collect data. The data can be qualitative data like Bubbles are produced. Or the data can be quantitative data like 32.4 mL of gas were produced. Quantitative data are acquired through measurement. The measurements result in numerical information. Chemistry is a science that has a strong numerical basis.
 
Chemistry is often said to be a quantitative science. Chemistry students will encounter many concepts and ideas that are numerical in nature. Mass, volume, energy, rate, concentration, and rate are examples of concepts that have a numerical side to them. A solution of acid could be said to be highly concentrated; this is a qualitative statement. The same solution of acid could be described as a 4.5-molar solution. This is a quantitative statement. A quantitative statement uses a numerical value to describe an observation or phenomenon. Chemistry is a quantitative science because its concepts and ideas can be described in numerical terms.
 

 
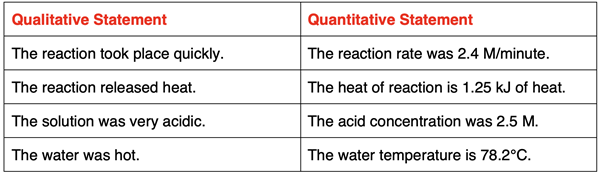
A quantitative science relies on mathematics. Much of the course is devoted to discovering patterns in chemical behavior. These patterns are often expressed using the language of mathematics. Graphs and charts, equations and formulas, and numerical problems are a common feature of most Chemistry courses. If you walk into a Chemistry classroom on any given day, a calculator on every desk would be a common observation. Chemistry is a quantitative science; numbers are part of its language.
 

 
 

Numbers – Big and Small

Much of the quantitative information in a Chemistry course will include numbers that are very big or very small. Consider the following Chemistry statements.
 

• A typical penny contains approximately 3900000000000000000000 atoms of copper.
• A hydrogen atom has a mass of 0.00000000000000000000000167 grams.
• The time for one-half of a uranium sample to decay is 22000000000000000 seconds.
• A carbon dioxide molecule has a length of approximately 0.000000033 centimeters.

 
Number like the ones above are cumbersome to work with because of the large number of trailing or leading zeroes. Most of these numbers cannot even be entered into a scientific calculator. Surely there is a better way of managing such numbers. Fortunately, there is.
   
 

Scientific Notation

Both large and small numbers are often expressed in scientific notation. Scientific notation is often referred to as exponential notation. Scientific notation is a format for expressing a number while often avoiding leading or trailing zeroes. Scientific notation represents a number in the format.
   
where C is a number between 1 and 10 and n is a positive or negative integer.
 
You will need to gain a comfort with its use and acquire the skill of converting a number from standard decimal notation to scientific notation. The table below shows several examples of the two formats for expressing large and small numbers.

 

Converting from Decimal Notation to Scientific Notation

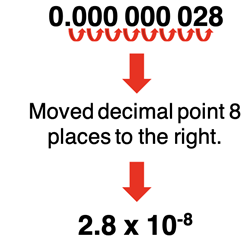
Use the following steps to convert from standard decimal notation to scientific notation.

1. Move decimal point until there is one digit to the left of the decimal point.
2. Count the number of places the decimal point was moved; note the direction the decimal point is moved.
3. Multiply the resulting decimal by 10ⁿ where n is the number of decimal places. n is positive if the decimal point was moved leftward. n is negative if the decimal point was moved rightward.

 
 
 
 
 

Converting from Scientific Notation to Decimal Notation

Use the following steps to convert from scientific notation to standard decimal notation.

1. For a positive exponent on 10, move the decimal point to the right a number of places equal to the exponent. Add trailing 0s if necessary (as placeholders).
2. For a negative exponent on 10, move the decimal point to the left a number of places equal to the exponent. Add leading 0s if necessary (as placeholders).
3. Remove the x 10ⁿ part from the number.

 
 
 
 






 

 
 

Calculators and Scientific Notation

Perhaps the most difficult aspect of using scientific notation is the task of entering such a value into your calculator. Not all calculators are equal. Most scientific and graphing calculators have buttons that allow you to enter a number in scientific notation. Consider the speed of light – 299790000 m/s. When converted to scientific notation, this quantity would be 2.9979 x 10⁸ m/s. To enter the number in scientific notation, type in the 2.9979 (everything before the multiply sign). Then tap on the EE or EXP button on the function pad of the calculator. A 00 appears to the right of 2.9979 on the LCD display of your calculator. This 00 represents the exponent on 10. Enter 08. Done! Note that you never need to use the multiply sign. The calculator takes care of the multiply sign when you tap the EE or EXP button.
 
 
 




 

Before You Leave ...

1. Download our Study Card on Scientific Notation. Save it to a safe location and use it as a review tool.
2. Consider some practice - try the second activity of our Measurement and Numbers Concept Builder. It's titled Scientific Notation.