Lesson 3: Measurements in Chemistry

Part a: Precision and Uncertainty

Part 3a: Precision and Uncertainty
Part 3b: Significant Digits
Part 3c: Evaluating Results
 
 

Three Traits of a Measurement

We learned in Lesson 1 that Chemistry is a lab science. And we learned in Lesson 2 that Chemistry is a quantitative science. So, count on two things: there will be measurements; there will be numbers.
 
A measurement involves more than a number. There are three types of information included in every measurement. Not a single one of these is more important than the other. The three traits of every measurement are the …

1. Numerical value
2. Unit of measurement
3. Degree of precision

 
Let’s suppose a lab notebook includes the following entry:
 

Mass of Empty Beaker = 122.50 gram

 
In this reported measurement, the numerical value is 122.50. This is the easy part; no student ever ignores this. The unit of measurement is the gram. Units were discussed in Lesson 2. Units are essential. Failing to include units in Chemistry class is equivalent to writing a sentence in English class that doesn’t have any nouns. You would never write a sentence in the form of A tall walked down the long and entered the convenient to purchase three. Such a sentence is incomprehensible. In the same way, the chemistry statement Mass of Empty Beaker = 122.50 is equally incomprehensible. Units are essential in the same way that nouns are essential.

 
In this part of Lesson 3, we will focus on the third trait of a measurement – the degree of precision. This refers to how many decimal places to which we reliably know the amount. The mass of the reported beaker is known reliably to the second decimal place. We know this because the amount is reported to two decimal places. The 0 at the end of the reported value is significant. The measurement, likely made by an electronic balance, is capable of measuring mass to the hundredths decimal place.
 
 

If a student were to drop the trailing 0 when recording the measurement, then they would be indicating that the device used to make the measurement was only reliable to the first decimal place. The amount 122.5 may be numerically equivalent to the amount 122.50. However, the precision to which these two reported measurements express the amount is different. When it comes to the degree of precision, 122.5 ≠ 122.50. If electronic balances had feelings (and perhaps they might), then they would view the dropping of the trailing 0 as an insult. It would be akin to saying "Hey $200 electronic balance dude! You're no better than my $15 electronic balance." Those are insulting words and you ought to mind your manners (and trailing zeroes) a bit more than that!
 

 

 

Instrument Precision

The degree of precision pertains to how many digits (or decimal places) are allowed by the measuring tool. Electronic instruments, such as electronic balances and digital thermometers, will make the decision for you regarding the degree of precision. Simply record as your measurement all the digits on the LCD display.
 
Many instruments you use in Chemistry lab will not be electronic. The instrument will include a measuring scale with markings and digits. The markings on the instrument provide a level of certainty to the measurement. A scale with very few markings is not capable of making a very precise measurement. But a scale with many markings allows for more precise measurements. A close-up view of two graduated cylinders (for measuring liquid volumes) is shown below.
 

 

 
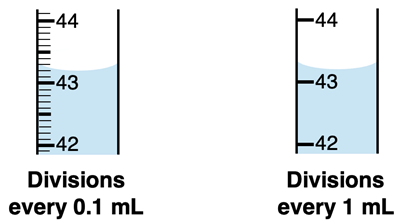
The scale of the instrument on the left allows for a more precise measurement. The instrument on the left has markings every 0.1-mL. This allows you to be certain of any measurement to 0.1 mL. Beyond, the tenths decimal place, you are estimating a volume. If you report a volume measurement to the hundredths decimal place, the digit in the hundredths place is not a certain digit. The instrument on the right has markings every 1-mL. You can be certain of your measurement to the mL; beyond that you’re estimating. If you report a volume measurement to the tenths decimal place, the digits in the tenths place is an estimated digit and not a certain digit.
 
 
 

The Estimated Digit and Uncertainty

Every measurement is composed of certain digits and one estimated digit. The graduated cylinder at the right has markings every 0.1 mL. This allows you to be certain of your measurement to the tenths decimal place. The volume (read from the bottom of the meniscus or curve) is certainly somewhere between 24.2 mL and 24.3 mL. So, the proper measurement would be 24.2X mL where X is an estimated digit. Reporting 24.2 mL as the measurement fails to include the estimated digit. Acceptable measurements could be reported as 24.23 mL, 24.25 mL, 24.26 mL, 24.28 mL, etc. All acceptably reported measurements would include an estimated digit in the hundredths decimal place.
 
Because the measurement contains an estimated digit, there is uncertainty associated with the measurement. When required, the uncertainty can be expressed by adding a ±Y after the reported measurement. Here, Y represents the uncertainty. The conventional practice is that Y is equal to one-half of the spacing between the markings on the instrument. If the markings on the scale are spaced apart by 0.1 mL, then the uncertainty is one-half of 0.1 mL. The diagram at the right has markings every 0.1 mL, so the uncertainty is 0.05 mL. Expressing the volume measurement might look like this:

 
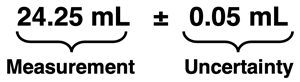
Reporting the measurement in this manner is equivalent to saying:

I’m certain of the first three digits. My fourth digit is an estimate and therefore uncertain. In reporting the measurement, I could be off by as much as 0.05 mL in either direction.

 

 

 

The Tale of Two Balances

One of the take-home messages from this page is that the instrument determines the degree of precision of a measurement. And it is important when reporting a measurement to report it in a manner that reflects the degree of precision to which the measurement is reliably known.
 
Suppose that you were to scoop some chemicals into my gloved hand. I might be able to feel it and report that the mass is about 10 grams. That's not too precise. As a measuring instrument, my gloved hand is rather blunt. The gloved-hand-balance is incapable of sharp and keen discernment of the mass and has a large uncertainty. A typical balance in a Chemistry lab might report the same scoop to have a mass of 9.85 gram. This is a much more precise measurement with a small uncertainty. We wouldn't say that one measuring tool is more accurate than the other; rather we would say that one measuring tool is more precise than the other.

 
 

The Significance of Zeroes

Let's suppose for a moment that an electronic balance measured the mass of a scoop of chemicals to be 10.00 g. How would you report the value? Answer: exactly what you read ... because any measurement made by an instrument not only reports the amount but also the degree of precision. If you reported 10 g as the mass of the scoop, you would be insulting the electronic balance. Discarding the last two digits is like treating the electronic balance as having no more awareness of mass measuring than the palm of a gloved hand. For a balance that costs a few hundred dollars, that's an insult!
 
If you’re a thinking student, then you might reply ...

Wait! There's no difference between 10 and 10.00; so what's it matter?

 
We will have to agree that if we are talking about the amount (the first trait of a measurement), then there is no difference between 10 and 10.00. But the discussion of this page isn't about amount. This discussion pertains to precision. And when it comes to precision, there's a couple hundred dollars of difference between 10 and 10.00. The 10.00 g measurement is made by a $200-$300 electronic balance. The 10 g measurement is made by a hand equipped with a 20-cent glove. The three additional significant digits reported in the 10.00 measurement signify that the instrument used to make the measurement reports reliably to the second decimal place.
 
The fact is that these trailing zeroes showing up in the first, second, third decimal place, like any other digit, are significant. It is doubtful that a student would ignore a 2 or a 3 if it showed up as the last digit on the LCD display of an electronic balance. Nobody ever annihilates an 8 or a 9 digit. Why eliminate the 0? The trailing zeroes in a measurement reveal information about the degree of precision to which the measured value is known. That's significant information!
 
Zeroes matter! Sadly … every day students ignore the 0s on their measurements, discounting them, discarding them, ignoring them, and considering them to be insignificant beings in the world of digits. It’s time to stop this moral atrocity and to consider the significance of zeroes. Stand up for zeroes!
 

 
 

 
 

Before You Leave

1. Consider some practice - try the third activity of our Measurement and Numbers Concept Builder; it's titled Measurement. 
2. And while you're at it, try the third activity of our Lab Procedures Concept Builder; it's also titled Measurement.
3. We know it is hard to stop once you get started, so try the second activity of our Significant Digits and Measurement Concept Builder. It might surprise you, but it's titled Measurement.

 

Check Your Understanding

Use the following questions as an assessment of your understanding. Tap the Check Answer buttons when ready.
 
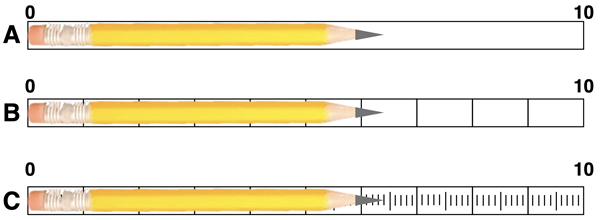
1. Suppose that you’re measuring the length of a pencil using three different centimeter rulers. What measurement would you report with each ruler? What is the uncertainty for each measurement?

 

 

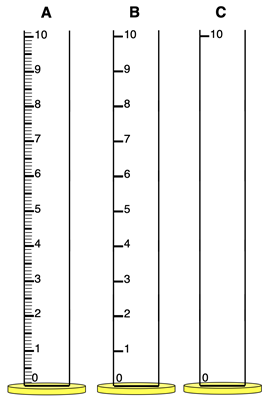
2. Consider the measurement given for the volume of a solution.

6.2 mL

Assuming that it is correctly reported, which one of the following graduated cylinders was used in making the measurement? Why did you choose what you did?

 

 
 
 

3. What volume would you report for the graduated cylinder at the right? And what would be the uncertainty?