Lesson 4: Kinetic Molecular Theory

Part b: Explaining Ideal Gas Behavior

The Particle Model

On the previous page of Lesson 4, we discussed the Kinetic Molecular Theory (KMT). KMT provides a particle-level model for explaining the behavior of an ideal gas. The particles are atoms for gaseous elements like Ne, Ar, Kr, etc. and molecules for compounds like CO₂, NO, SO₂, and HCl and diatomic elements like O₂, N₂, and Cl₂. In this part of Lesson 4, we will use an understanding of particle behavior to explain several of the gas laws discussed in Lesson 2.
 
 
 

Boyle’s Law

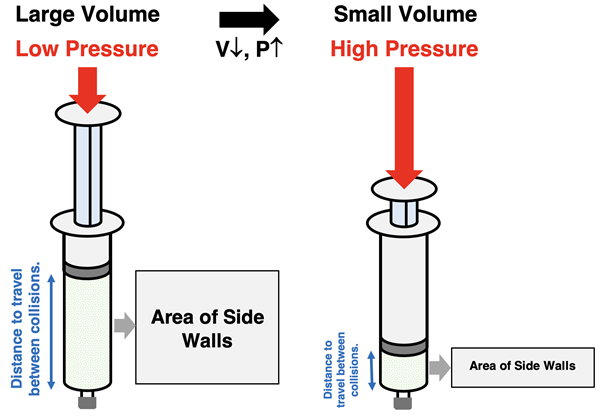
Boyle’s Law describes the relationship between pressure and volume for a sample of gas held at a constant temperature and number of moles. The law states that the pressure and volume are inversely proportional. As the volume of a sample of gas decreases, the pressure is observed to increase. How is this pattern explained using KMT?
 
Pressure is the result of particles colliding with the container walls and applying force to the walls. Mathematically, pressure is the ratio of the cummulative amount of force per surface area of the container. Two factors contribute to the increase in pressure as the volume decreases. The first factor is that the surface area of the container decreases. The second factor is that collisions occur more frequently in a smaller container. In a smaller container, the distance from one side of the container to the other is shorter and a particle will travel from one wall to the other wall in less time. This results in a higher collision frequency and more cummulative force on the wall. By decreasing area and increasing force, there will be an increase in pressure.

Gay Lussac’s or Amontons’ Law

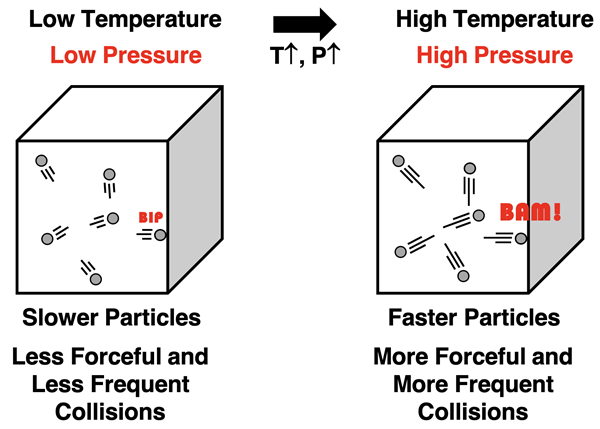
Gay Lussac’s Law (a.k.a., Amontons’ Law) describes the relationship between pressure and Kelvin temperature for a sample of gas held at a constant volume and number of moles. The law states that the pressure and temperature are directly proportional. As the Kelvin temperature of a sample of gas increases, the pressure is observed to increase. How is this pattern explained using KMT?
 
One of the postulates or assumptions of kinetic molecular theory is that the average kinetic energy of particles is directly proportional to the Kelvin temperature. So if the temperature is increased, particles move with a greater kinetic energy. The kinetic energy is the energy of motion and dependent upon particle speed. So at higher temperatures, particles are moving faster. This impacts the pressure for two reasons. Faster particles will have more forceful collisions with the container walls. And faster particles will have more frequent collisions with container walls since they travel from wall to wall in less time. Both of these factors increase the amount of force upon the container walls. With the volume held constant, there is no change in surface area of the walls. Since pressure is directly related to the force on the wall, an increase in Kelvin temperature causes an increase in pressure.

Charles’ Law

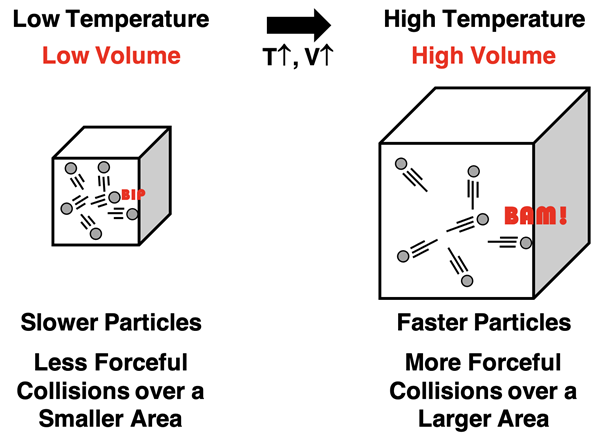
Charles’ Law describes the relationship between volume and Kelvin temperature for a sample of gas held at a constant pressure and number of moles. The law states that the volume and temperature are directly proportional. As the Kelvin temperature of a sample of gas increases, the volume is observed to increase. How is this pattern explained using KMT?
 
We begin again with the assumption that the average kinetic energy of particles is directly proportional to the Kelvin temperature. So if the temperature is increased, particles move with a greater kinetic energy. That is, they move faster at higher temperatures and have more forceful collisions with the container walls. Based on the Pressure-Force-Area relationship (equation at right), more force would result in more pressure. But Charles’ law is based on constant pressure conditions. The only way for that the pressure could stay constant is if the container expands in volume and its walls be of greater area. With more forceful collisions on walls that have a greater area, the pressure can remain constant. Thus at a constant pressure, an increase in Kelvin temperature leads to an increase in volume.

Avogadro’s Law

Avogadro’s Law describes the relationship between volume and number of moles for a sample of gas held at a constant pressure and temperature. The law states that the volume and number of moles of gas are directly proportional. As the number of moles of gas particles increases, the volume of the gas is observed to increase. How is this pattern explained using KMT?
 
We begin with the definition of pressure as the force per area. Each collision that occurs between a gas particle and the container wall contributes to the force on the container walls. With more particles of gas in the container, collisions occur more frequently and resut in a greater amount of force. But Avogadro’s law includes the restriction that the pressure remains constant. The only means by which the pressure can remain constant when the force increases is for the area to increase proportionally. Thus, the container volume increases. This increases the area of the container and maintains a constant pressure.

Conlusion

The Kinetic Molecular Theory (KMT) provides a simple model of gas particles that explains the relationship between state variables for an ideal gas. The foundation of the theory are five postulates or assumptions about particles of an ideal gas. But what if one or more of those assumptions turned out to be quite contrary to reality. For instance, what if particles did exert attractive forces upon one another as they move about the container? Or what if the particles of a gas weren’t points in space but had a finite volume? These questions will be explored on our final page of Lesson 4 as we discuss the limitations of the Kinetic Molecular Theory.
 
 
 

Before You Leave

• Download our Study Card on Kinetic Molecular Theory. Save it to a safe location and use it as a review tool. (Coming Soon.)
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 

Questions coming soon.