Light Waves and Color Review
Navigate to:
Review Session Home - Topic Listing
Light Waves and Color - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-#11 || #12-#20 || #21-#28
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
Part A: Multiple Choice
1. Which of the following statements are true statements about interference?
- Interference occurs when two (or more) waves meet while traveling along the same medium.
- Interference can be constructive or destructive.
- Interference of two waves at a given location results in the formation of a new wave pattern which has a greater amplitude than either of the two interfering waves.
- The meeting of a trough of one wave with a trough of another wave results in destructive interference.
- The only way for two waves to interfere constructively is for a crest to meet a crest or a trough to meet a trough.
- It is only a theory that light can interfere destructively; the theory is based on the assumption that light is a wave and most waves exhibit this behavior. Experimental evidence supporting the theory has not yet been observed.
|
Answer: AB
A - True: This is the definition of interference - "the meeting of two or more waves along the same medium."
B - True: These are the two possible types of interference.
C - False: When interference occurs, there are two possible results: a resulting wave with a greater displacement than either of the original waves (constructive interference) or a resulting wave with a smaller displacement than one or both of the original waves (destructive interference)
D - False: This is an example of constructive interference leading to a resulting wave with a greater displacement than the individual wave; a "super-trough" would be formed.
E - False: Crest meeting crest and trough meeting trough are examples of constructive interference. These special cases result in the formation of antinodal points - points of maximum displacement. But more generally, constructive interference will occur anytime a wave with a "positive" (up or right or ...) displacement meets another wave with a "positive" displacement OR when a wave with a "negative" (down or left or ...) displacement meets another wave with a "negative" displacement. When the displacements of the two interfering waves are in the same direction at a given point, then constructive interference occurs at that point.
F - False: There is plenty of experimental and observable evidence that light undergoes destructive interference. The best evidence from our studies in class are the dark fringes of a two-point interference pattern. These dark fringes are the result of the destructive interference of light.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
2. Which of the following statements are true statements about two-point light source interference patterns?
- Two-point light source interference patterns consist of alternating nodal and antinodal lines.
- If projected onto a screen, two-point light source interference patterns would be viewed as alternating bright and dark spots with varying gradients of light intensity in between.
- As the distance between the sources is decreased, the distance between the nodal and antinodal lines is decreased.
- As the wavelength of the laser light is decreased, the distance between the nodal and antinodal lines is decreased.
- A nodal point would be formed if a trough of one wave meets a trough of another wave.
- Antinodal points are points where the medium is undergoing no vibrational motion.
- Suppose point P is a point where a wave from one source travels a distance of 2.5 wavelengths before meeting up with a wave from another source which travels a distance of 3.5 wavelengths. Point P would be a nodal point.
- Suppose point Q is a point where a wave from one source travels a distance of 2 wavelengths before meeting up with a wave from another source which travels a distance of 3.5 wavelengths. Point Q would be a nodal point.
- Suppose point R is a point where a wave from one source travels a distance of 2 wavelengths before meeting up with a wave from another source which travels a distance of 3 wavelengths. Point R would be a nodal point.
- If the path difference for points on the first nodal line is 4 cm, then the wavelength would be 6 cm. (NOTE: the first nodal line is considered to be the first nodal line to the left or right from the central antinodal line.)
|
Answer: ABDH
A - True: This is exactly what we have observed through computer animations, video segments, transparency overlays, and the actual experiment.
B - True: This is exactly what we observed when we performed Young's experiment.
C - False: The equation relating the variables of Young's experiment can be rearranged to the following form:
y = m • L • W / d ... (where W=wavelength).
Now one notices that y is inversely related to d. So if the slit separation distance (d) is decreased, the distance between nodal and antinodal lines (related to y) would be increased.
D - True: Young's equation is often written as
W = y • d / (m • L) ... (where W=wavelength).
From the equation, one notices that wavelength (W) is directly related to y. So if the wavelength (W) is decreased, the distance between nodal and antinodal lines (related to y) would be decreased.
E - False: Antinodal points are points of maximum displacement; for a light interference pattern, these are the brightest points.
F - False: Nodal points are points of no displacement or no disturbance; for a light light interference pattern, these are the darkest points.
G - False: In this case the path difference is 1 wavelength; when two waves traveling to the same point have a difference in distance traveled of 1 wavelength, then a crest of one wave would meet up with a crest of the second wave. This condition leads to constructive interference and an antinodal point is formed.
H - True: In this case the path difference is 1.5 wavelengths; when two waves traveling to the same point have a difference in distance traveled of 1.5 wavelengths, then a crest of one wave would meet up with a trough of the second wave. This condition leads to destructive interference and a nodal point is formed.
I - False: In this case the path difference is 1 wavelength; when two waves traveling to the same point have a difference in distance traveled of 1 wavelength, then a crest of one wave would meet up with a crest of the second wave. This condition leads to constructive interference and an antinodal point is formed.
J - False: The first nodal line is designated as m = 0.5; the path difference is 4 cm. Substituting into the equation PD = m•Wavelength and solving for wavelength yields a value of 8 cm.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
3. Which of the following statements are true statements about nodal and antinodal points in light interference patterns?
- Antinodes result from constructive interference.
- Nodes result from destructive interference.
- The nodal points on an interference pattern are positioned along lines; these lines are called nodal lines.
- The central line on the interference pattern is a nodal line.
- Points on nodal lines would be represented by bright spots if projected onto a screen.
- The path difference for points on the central antinodal line would be 0.
- The path difference for points on the first antinodal line would be 1 cm.
- (This question presumes that the interference pattern is a water interference pattern.) If the path difference for points on the first antinodal line is 5 cm, then the path difference for points on the second antinodal line would be 7 cm.
- (This question presumes that the interference pattern is a water interference pattern.) If the path difference for points on the first antinodal line is 5 cm, then the path difference for points on the third antinodal line would be 15 cm.
- (This question presumes that the interference pattern is a water interference pattern.) If the path difference for points on the first antinodal line is 6 cm, then the path difference for points on the second nodal line would be 9 cm. (NOTE: the second nodal line is considered to be the second nodal line to the left or right from the central antinodal line.)
- (This question presumes that the interference pattern is a water interference pattern.) If the path difference for points on the first nodal line is 4 cm, then the path difference for points on the third nodal line would be 12 cm. (NOTE: the third nodal line is considered to be the third nodal line to the left or right from the central antinodal line.)
|
Answer: ABCFIJ
A - True: An antinode is a point where a crest meets a crest or a trough meets a trough; both are examples of constructive interference.
B - True: A node is a point where a crest meets a trough; this is an example of destructive interference and leads to a location of no displacement.
C - True: Nodal points all lie along lines. Question #21 illustrates this well.
D - False: The central line - that is, the line extending outward from the midpoint between the two sources - is a line upon which antinodes are formed; it is called an antinodal line. Question #21 illustrates this well.
E - False: Nodal lines are formed as a result of destructive interference. If projected onto a screen, the nodal points would appear as the darkest points on the interference pattern.
F - True: The path difference for points on the central antinodal line would be given be the equation: PD = m•W where W=wavelength and m=0 (for the central antinodal line). Substituting into this equation yields PD = 0•W which would be 0.
G - False: The path difference for points on the first antinodal line would be given be the equation: PD = m•W where W=wavelength and m=1 (for the first antinodal line). So the path difference for the first antinodal line would always be 1•W; but it would only be 1 cm for the case in which the wavelength is 1 cm.
H - False: The first antinodal line is numbered as the m=1 line. The path difference relates to the wavelength (W) by the equation PD = m•W. Substituting m=1 and PD=5 cm into this equation yields a wavelength value of 5 cm. The second antinodal line is numbered as the m=2 line. Re-using the equation for this line with m=2 and W=5 cm yields a path difference of 10 cm.
I - True: The first antinodal line is numbered as the m=1 line. The path difference relates to the wavelength (W) by the equation PD = m•W. Substituting m=1 and PD=5 cm into this equation yields a wavelength value of 5 cm. Re-using the equation for the third antinodal line with m=3 and W=5 cm yields a path difference of 15 cm.
J - True: The logic on this question is similar to the above question. The first antinodal line is numbered as the m=1 line. The path difference relates to the wavelength (W) by the equation PD = m•W. Substituting m=1 and PD=6 cm into this equation yields a wavelength value of 6 cm. The second nodal line is numbered as m=1.5. Re-using the equation for the second nodal line with m=1.5 and W=6 cm yields a path difference of 9 cm.
K - False: The first nodal line is numbered the m=0.5 line. If the path difference for a point on this line is 4 cm, then the wavelength is 8 cm (using the PD = m•W equation). The third nodal line is numbered as the m=2.5 line. Using the same equation to find the path difference yields a value of 20 cm.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
4. Which of the following statements are true statements about Thomas Young's experiment?
- Young's experiment provided evidence that light exhibits particle-like behavior.
- Young's experiment depends upon the use of white light from two sources.
- The two sources of light in Young's experiment could be two different light bulbs.
- For Young's equation to be geometrically valid, the distance from the sources to the screen must be much greater than the slit separation distance.
- For Young's equation to be geometrically valid, the wavelength of the light must be much greater than the slit separation distance.
- Thomas Young measured the distance from an antinodal point (of known number) to each of the two sources, computed a path difference and calculated the wavelength of light.
- Thomas Young was able to determine the wavelength of a light wave.
|
Answer: DG
a. - False: Young's experiment supports the wave-nature of light. Waves interfere and Young's experiment provided clear evidence that light undergoes interference.
b. - False: There are two requirements for the light which is utilized in Young's experiment: the two light sources must be coherent and monochromatic. Monochromatic means that the light sources must provide light of the same wavelength (and a single wavelength); using a white light bulb would produce light of many wavelengths. Second, coherent means that the light from the two sources must be vibrating together, experiencing a crest at the same time and a trough at the same time. Using two light bulbs (as opposed to a single light source shining on a double slit) would likely result in incoherent light.
c. - False: If two light bulbs emitting monochromatic light of the same color were used, one of the two requirements would be met. Yet there would still be the problem of incoherence. See explanation to part b.
d. - True: There are two geometric requirements for Young's experiment: the screen distance (L) must be much greater than the slit separation distance (d) and the slit separation distance must be much greater than the wavelength. That is L >>> d and d >>> W.
e. - False: Vice versa; d >>> W. See explanation to part d.
f. - False: Thomas Young used the equation W = y•d/m•L. Measurement of y, d, m, and L is much more practical since the size of these quantities is much larger. The error introduced in the measurement would not overwhelm the precision of the wavelength measurement. On the other hand, a measurement of the path difference would be very difficult since the only way to achieve this measurement is to measure the two distances. Given the fact that the slits are so close together, these two distances are so nearly identical that the error introduced in the measurement of one distance would overwhelm the actual difference in distance between the two measurements. That's why Young had to derive the equation W = y•d/m•L.
g. - True: Measuring the wavelength of a visible light wave was one of the main outcomes of Young's experiment.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
5. Light which is vibrating in a single plane is referred to as _____ light
|
a. electromagnetic
|
b. transverse
|
c. unpolarized
|
d. polarized
|
|
Answer: D
Unpolarized light is light whose vibrations are in a multitude of directions. To simplify matters, unpolarized light is light which can be thought of as vibrating in a vertical and a horizontal plane. If one of these planes of vibration is removed, then light would be vibrating in a single plane and said to be "polarized."
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
6. Light which is vibrating in a variety of planes is referred to as _____ light
|
a. electromagnetic
|
b. transverse
|
c. unpolarized
|
d. polarized
|
|
Answer: C
Unpolarized light is light whose vibrations are in a multitude of directions.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
7. Light usually vibrates in multiple vibrational planes. It can be transformed into light vibrating in a single plane of vibration. The process of doing this is known as ____.
|
a. translation
|
b. interference
|
c. polarization
|
d. refraction
|
|
Answer: C
Polarization is defined as the process of transforming unpolarized light (light whose vibrations are in a multitude of planes) into polarized light (light which can be thought of as vibrating in a single plane).
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
8. Light is passed through a Polaroid filter whose transmission axis is aligned horizontally. This will have the effect of ____.
a. making the light one-half as intense and aligning the vibrations into a single plane.
b. aligning the vibrations into a single plane without any effect on its intensity.
c. merely making the light one-half as intense; the vibrations would be in every direction.
d. ... nonsense! This will have no effect on the light itself; only the filter would be effected.
|
Answer: A
Polaroid filters have the effect of polarizing light - that is, aligning their vibrations into a specific plane. They can be thought of as performing this feat by removing the vibrations which occur within a plane perpendicular to the transmission axis.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
9. Light is passed through a Polaroid filter whose transmission axis is aligned horizontally. It then passes through a second filter whose transmission axis is aligned vertically. After passing through both filters, the light will be ______.
|
a. polarized
|
|
b. unpolarized
|
|
|
c. entirely blocked
|
|
d. returned to its original state.
|
|
Answer: C
The first filter serves the role of blocking one-half the light; the horizontal vibrations would emerge from the filter and the vertical vibrations would be blocked. The second filter would allow the vertical vibrations to pass through if there were any. However, since the vertical vibrations have already been filtered out, there is no light remaining after the second filter is used. This combination of two filters serves to block all the light.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
10. Which of the following are effective methods of polarization? Include all that apply.
a. Passing light through a Polaroid filter.
b. Reflection of light off a nonmetallic surface.
c. Passing light from water to air.
d. Passing light through a birefringent material such as Calcite.
e. Turning the light on and off at a high frequency.
f. Interfering light from one source with a second source.
|
Answer: AB
The use of a filter, the reflection of light off nonmetallic surfaces and the use of a birefringent material are all means of polarizing light. Refraction at an air-water surface would change the speed and the direction of light but would not have any effect upon its vibrational orientation. Turning a light on and off at a high frequency would only annoy or impress those present in the room. And light interference could create a pattern of bright and dark spots but would not have any effect upon light's vibrational orientation.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
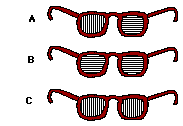 11. Consider the three pairs of sunglasses to the right. Which pair of glasses is capable of eliminating the glare from a road surface? (The transmission axes are shown by the straight lines.)
11. Consider the three pairs of sunglasses to the right. Which pair of glasses is capable of eliminating the glare from a road surface? (The transmission axes are shown by the straight lines.)
|
Answer: C
When light reflects off a road surface, a portion of the light vibrations becomes oriented in a plane which is horizontal to the road surface. This polarization often leads to an annoying glare. The glare can be reduced by blocking the polarized light. Since the light is polarized horizontally (assuming a horizontal road way - a good assumption), the sunglasses should be capable of blocking horizontal light and allowing the vertical vibrations to be transmitted. Selecting sunglasses C would make accomplish this feat.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
12. TRUE or FALSE:
White and black are actual colors of light.
|
Answer: B
Black is the absence of all light. Things appear black when they do not reflect or emit light. White is the presence of all colors of visible light. Objects appear white when they reflect or emit all wavelengths of visible light (or at least three wavelengths - Red, Blue and Green - in equal intensity).
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
13. The three primary colors of light are ____.
|
a. white, black, gray
|
b. blue, green, yellow
|
|
c. red, blue, green
|
d. red, blue, yellow
|
|
e. ... nonsense! There are more than three primary colors of light.
|
|
Answer: C
Yes, you must know this one! It forms the basis of most of our logic and reasoning about color, light and the appearance of objects.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
14. The three secondary colors of light are ____.
|
a. cyan, magenta, green
|
b. cyan, magenta, and yellow
|
|
c. orange, yellow, violet
|
d. red, blue, yellow
|
|
e. ... nonsense! There are more than three secondary colors of light.
|
|
Answer: B
The secondary colors of light are those colors which are formed when two primary colors are mixed in equal amounts. Mixing blue and green light results in cyan light. Mixing red and blue light results in magenta light. And mixing red and green light results in yellow light.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
15. Combining red and green light (with equal intensity) makes ____ light; combining red and blue light (with equal intensity) makes ____ light; and combining blue and green light (with equal intensity) makes ____ light. Choose the three colors in respective order.
|
a. brown, purple, aqua
|
b. brown, magenta, yellow
|
|
c. yellow, magenta, brown
|
d. yellow, magenta, cyan
|
|
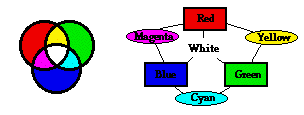 Answer: D Answer: D
You must know this for it forms the foundation of much of our reasoning. To assist in recalling the three primary colors of light, three secondary colors of light, and the means by which adding primaries form secondaries, develop some form of graphical reminder such as a color wheel or a diagram like those at the right.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
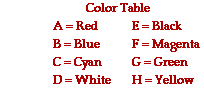 16. Demonstrate your understanding of color addition by completing the following color equations. Select colors from the Color Table at the right.
16. Demonstrate your understanding of color addition by completing the following color equations. Select colors from the Color Table at the right.
a. Red + Blue = _____
b. Red + Green = _____
c. Green + Blue = _____
d. Red + Blue + Green = _____
e. Blue + Yellow = _____
|
Answer: See table above.
A. Magenta is a secondary color of light formed by combining red light with blue light in equal amounts. Refer to graphic in previous question.
B. Yellow is a secondary color of light formed by combining red light with green light in equal amounts. Refer to graphic in previous question.
C. Cyan is a secondary color of light formed by combining green light with blue light in equal amounts. Refer to graphic in previous question.
D. White light is formed when all three primary colors of light are combined in equal amounts.
E. Yellow light is a combination of red and green light. So combining blue with yellow light is like combining blue light with red and green light. The result of combining these three primary colors of light is to produce white light.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
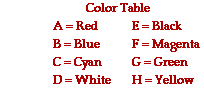 17. Demonstrate your understanding of color subtraction by completing the following color equations. Select colors from the Color Table at the right.
17. Demonstrate your understanding of color subtraction by completing the following color equations. Select colors from the Color Table at the right.
a. White - Blue = _____
b. White - Red = _____
c. White - Green = _____
d. White - Blue - Green = _____
e. White - Yellow = _____
f. Red + Green - Green = _____
g. Yellow - Green = _____
h. Yellow - Red = _____
i. White - Magenta = _____
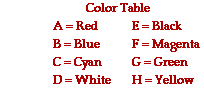 j. White - Cyan = _____
j. White - Cyan = _____
k. Yellow + Blue - Cyan = _____
l. Yellow + Cyan + Magenta = _____
m. Yellow + Cyan - Magenta = _____
n. Yellow + Cyan - Blue - Red = _____
|
Answer: See table above.
Each of these questions is best answered by first converting any secondary color of light into a mix of two primary colors of light. Then "do the arithmetic." If the result of the "arithmetic" is a combination of two primary colors, translate the combo into a secondary color of light. Here it goes:
a. White - Blue = R+G+B - B = R+G = Yellow
b. White - Red = R+B+G - R = G+B = cyan
c. White - Green = R+G+B - G = R+B = magenta
d. White - Blue - Green = R+G+B - B - G = R = red
e. White - Yellow = R+G+B - R+G = B = blue
f. Red + Green - Green = R + G - G = R = red
g. Yellow - Green = R+G - G = R = red (Note the similarity to part f.)
h. Yellow - Red = R+G - R = G = green
i. White - Magenta = R+G+B - R+B = G = green
j. White - Cyan = R+G+B - G+B = R = red
k. Yellow + Blue - Cyan = R+G + B - G+B = R = red
(Note the similarity to part j: R+G + B is the same as white; so this question is White - Cyan.)
l. Yellow + Cyan + Magenta = R+G + B+G + R+B = R+R+G+G+B+B = white + white (that is very bright white since there is double the red, green and blue added together)
m. Yellow + Cyan - Magenta = R+G + B+G - R+B = G+G = green
n. Yellow + Cyan - Blue - Red = R+G + G+B - B - R = G+G = green
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
18. Sunsets often have a reddish-orange color associated with them. This is attributable to the phenomenon of _____.
|
a. polarization
|
b. diffraction
|
c. dispersion
|
d. refraction
|
|
Answer: B
Sunsets are the result of the longer wavelengths of light diffracting around atmospheric particles and reaching our eyes, giving the reddish-orange appearance. More detail about the phenomenon can be accessed using the Useful Web Link below.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
19. A filter serves the function of ____.
a. subtracting color(s) from the light which is incident upon it
b. adding color(s) to the light which is incident upon it
c. removing nicotine from light so that we can live longer lives
d. confusing physics students who are studying color, causing them to live shorter lives
|
Answer: A
Filters can be thought of as absorbing one or more of the primary colors of light which are incident upon it, allowing remaining colors to be transmitted. For instance, a green filter will absorb all wavelengths except for green light. In this sense, filters subtract colors from the mix of incident light, allowing only selected colors to pass through.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
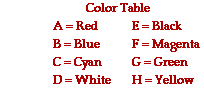 20. Express your understanding of filters by answering the following questions. Choose the best answer(s) from the Color Table shown at the right.
20. Express your understanding of filters by answering the following questions. Choose the best answer(s) from the Color Table shown at the right.
a. A red filter is capable of transmitting ____ light (if it is incident upon the filter).
b. A blue filter is capable of transmitting ____ light (if it is incident upon the filter).
c. A green filter is capable of transmitting ____ light (if it is incident upon the filter).
d. A red filter will absorb ____ light (if it is incident upon the filter).
e. A blue filter will absorb ____ light (if it is incident upon the filter).
f. A yellow filter will absorb ____ light (if it is incident upon the filter).
g. A magenta filter will absorb ____ light (if it is incident upon the filter).
h. A white object is illuminated with white light and viewed through a green filter. The object will appear _____.
i. A white object is illuminated with white light and viewed through a blue filter. The object will appear _____.
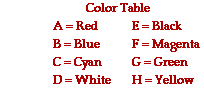 j. A white object is illuminated with white light and viewed through a cyan filter. The object will appear _____.
j. A white object is illuminated with white light and viewed through a cyan filter. The object will appear _____.
k. A blue object is illuminated with white light and viewed through a green filter. The object will appear _____.
l. A cyan object is illuminated with white light and viewed through a cyan filter. The object will appear _____.
m. A cyan object is illuminated with white light and viewed through a green filter. The object will appear _____.
n. A yellow object is illuminated with white light and viewed through a green filter. The object will appear _____.
o. A yellow object is illuminated with white light and viewed through a magenta filter. The object will appear _____.
p. A yellow object is illuminated with yellow light and viewed through a yellow filter. The object will appear _____.
q. A yellow object is illuminated with yellow light and viewed through a blue filter. The object will appear _____.
r. A yellow object is illuminated with blue light and viewed through a yellow filter. The object will appear _____.
s. A blue object is illuminated with blue light and viewed through a yellow filter. The object will appear _____.
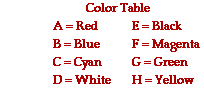 t. A yellow object is illuminated with yellow light and viewed through a red filter. The object will appear _____.
t. A yellow object is illuminated with yellow light and viewed through a red filter. The object will appear _____.
u. A yellow object is illuminated with yellow light and viewed through a green filter. The object will appear _____.
v. A yellow object is illuminated with green light and viewed through a yellow filter. The object will appear _____.
w. A yellow object is illuminated with green light and viewed through a green filter. The object will appear _____.
x. A yellow object is illuminated with green light and viewed through a red filter. The object will appear _____.
y. A yellow object is illuminated with green light and viewed through a cyan filter. The object will appear _____.
z. A red object is illuminated with yellow light and viewed through a cyan filter. The object will appear _____.
|
Answer: See sentences above.
Parts a-g target your understanding of the ability of filters to subtract colors of light from the mix of incident light that strikes it. A filter will absorb its complementary color of light. So a yellow filter absorbs blue light since blue is across from it on the color wheel. Whatever light is not absorbed will be transmitted; so yellow filters transmit red and green light (if incident upon it), also known as yellow light.
a. Red filters absorb cyan light (the complementary color of red). If white light (red + blue + green) shines on a red filter and cyan (blue + green) light is absorbed, all that is left to be transmitted is red light.
b. Blue filters absorb yellow light (the complementary color of blue). If white light (red + blue + green) shines on a blue filter and yellow (red + green) light is absorbed, all that is left to be transmitted is blue light.
c. Green filters absorb magenta light (the complementary color of green). If white light (red + blue + green) shines on a green filter and magenta (red + blue) light is absorbed, all that is left to be transmitted is green light.
d. Red filters absorb its complementary color - cyan. So this question could be answered as cyan. And since cyan light consists of blue + green light, this question could also be answered as blue + green.
e. Blue filters absorb its complementary color - yellow. So this question could be answered as yellow. And since yellow light consists of red + green light, this question could also be answered as red + green.
f. Yellow filters absorb its complementary color - blue. So this question must be answered as blue.
g. Magenta filters absorb its complementary color - green. So this question must be answered as green.
Parts h - z target your understanding of color subtraction for both pigments and filters. In each question, there is light incident upon an object. This light can be broken down into primary colors. Some light might be subtracted from this incident mix by either the object or the filter. The only possible color of light that could ultimately pass through the filter and effect the appearance of the object would be one of the primary colors in the incident light. For instance, suppose that an object is illuminated with yellow light (which is a combination of red and green primary colors of light. The object could appear yellow (if neither red nor green are subtracted away), or red (if green light subtracted is taken away) or green (if red light is subtracted away) or black (if both red and green light is subtracted away).
In the explanations below, each question will be approached by identifying the primary colors of light in the incident mix (the light used to illuminate the object) and then primaries will be successively subtracted away by the pigments in the object and by the filter. Here it goes:
h. RGB light (white light) hits a white object; white objects do not subtract (i.e., absorb) any colors; so RGB reflects off the object and heads towards a green filter. Green filters would subtract R and B (when present) and allow G to pass through. So RGB - nothing - GB = R = red.
i. RGB light (white light) hits a white object; white objects do not subtract (i.e., absorb) any colors; so RGB reflects off the object and heads towards a blue filter. Blue filters would subtract R and B (when present) and allow B to pass through. So RGB - nothing - RG = B = blue.
j. RGB light (white light) hits a white object; white objects do not subtract (i.e., absorb) any colors; so RGB reflects off the object and heads towards a cyan filter. Cyan filters would subtract R (when present) and allow G to pass through. So RGB - nothing - R = GB = cyan.
k. RGB light (white light) hits a blue object; blue objects subtract (i.e., absorb) R and G light (when present); so B light reflects off the object and heads towards a green filter. Green filters would subtract R and B (when present) and allow G to pass through; blue light is present so it will be subtracted. So RGB - GB - B = nothing = black.
l. RGB light (white light) hits a cyan object; cyan objects subtract (i.e., absorb) R light (when present); so GB light reflects off the object and heads towards a cyan filter. Cyan filters would subtract R (when present) and allow GB to pass through. So RGB - R = GB = cyan.
m. RGB light (white light) hits a cyan object; cyan objects subtract (i.e., absorb) R light (when present); so GB light reflects off the object and heads towards a green filter. Green filters would subtract RB (when present) and allow G to pass through; B is present so it will be subtracted. So RGB - R - B = G = green.
n. RGB light (white light) hits a yellow object; yellow objects subtract (i.e., absorb) B light (when present); so RG light reflects off the object and heads towards a green filter. Green filters would subtract RB (when present) and allow G to pass through; R is present so it will be subtracted. So RGB - B - R = G = green.
o. RGB light (white light) hits a yellow object; yellow objects subtract (i.e., absorb) B light (when present); so RG light reflects off the object and heads towards a magenta filter. Magenta filters would subtract G (when present) and allow RB to pass through; G is present so it will be subtracted. So RGB - B - G = R = red.
p. RG light (yellow light) hits a yellow object; yellow objects subtract (i.e., absorb) B light (when present); so RG light reflects off the object and heads towards a yellow filter. Yellow filters would subtract B (when present) and allow RG to pass through. So RG - nothing - nothing = RG = yellow.
q. RG light (yellow light) hits a yellow object; yellow objects subtract (i.e., absorb) B light (when present); so RG light reflects off the object and heads towards a blue filter. Blue filters would subtract RG (when present) and allow B to pass through; R and G are both present so they will be subtracted. So RG - nothing - RG = nothing = black.
r. B light (blue light) hits a yellow object; yellow objects subtract (i.e., absorb) B light (when present); so no light light reflects off the object and it wouldn't matter what type of filter is used. This object will appear black. So B - B - nothing = nothing = black.
s. B light (blue light) hits a blue object; blue objects subtract (i.e., absorb) RG light (when present); so B light reflects off the object and heads towards a yellow filter. Yellow filters would subtract B (when present) and allow RG to pass through (if present); neither R nor G are present and the B gets subtracted. So B - nothing - B = nothing = black.
t. RG light (yellow light) hits a yellow object; yellow objects subtract (i.e., absorb) B light (when present); so RG light reflects off the object and heads towards a red filter. Red filters would subtract GB (when present) and allow R to pass through (if present); G is present so it gets subtracted. So RG - nothing - G = R = red.
u. RG light (yellow light) hits a yellow object; yellow objects subtract (i.e., absorb) B light (when present); so RG light reflects off the object and heads towards a green filter. Green filters would subtract RB (when present) and allow G to pass through (if present); R is present so it gets subtracted. So RG - nothing - R = G = green.
v. G light (green light) hits a yellow object; yellow objects subtract (i.e., absorb) B light (when present); so G light reflects off the object and heads towards a yellow filter. Yellow filters would subtract B (when present) and allow RG to pass through (if present). So G - nothing - nothing = G = green.
w. G light (green light) hits a yellow object; yellow objects subtract (i.e., absorb) B light (when present); so G light reflects off the object and heads towards a green filter. Green filters would subtract RB (when present) and allow G to pass through (if present). So G - nothing - nothing = G = green.
x. G light (green light) hits a yellow object; yellow objects subtract (i.e., absorb) B light (when present); so G light reflects off the object and heads towards a red filter. Red filters would subtract GB (when present) and allow R to pass through (if present); G is present so it gets subtracted. So G - nothing - G = nothing = black.
y. G light (green light) hits a yellow object; yellow objects subtract (i.e., absorb) B light (when present); so G light reflects off the object and heads towards a cyan filter. Cyan filters would subtract R (when present) and allow GB to pass through (if present). So G - nothing - nothing = G= green.
z. G light (green light) hits a red object; red objects subtract (i.e., absorb) GB light (when present). G is present so it gets subtracted and it wouldn't matter what filter is used to view this object; there is no light reflecting off the object so it will appear black. So G - G - nothing = nothing = black.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
Part B: Diagramming, Analysis, Calculations
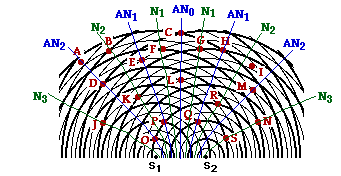 21. Two point sources are vibrating together (in phase) at the same frequency to produce a two-point source interference pattern. The diagram at the right depicts the two-point source interference pattern. The crests are represented by thick lines and the troughs by thin lines. Several points on the pattern are marked by a dot and labeled with a letter. Use the diagram to answer the following questions.
21. Two point sources are vibrating together (in phase) at the same frequency to produce a two-point source interference pattern. The diagram at the right depicts the two-point source interference pattern. The crests are represented by thick lines and the troughs by thin lines. Several points on the pattern are marked by a dot and labeled with a letter. Use the diagram to answer the following questions.
a. Which of the labeled points are antinodal points?
b. Which of the labeled points are nodal points?
c. Which of the labeled points are formed as a result of constructive interference?
d. Which of the labeled points are located on the central antinodal line?
e. Which of the labeled points are located on the first antinodal line?
f. Which of the labeled points are located on the second antinodal line?
g. Which of the labeled points are located on the third antinodal line?
h. Which of the labeled points are located on the first nodal line (using the notation that the first nodal line is the nodal line directly to the left or the right of the central antinodal line)?
i. Which of the labeled points are located on the second nodal line (using the notation that the second nodal line is the second nodal line directly to the left or the right of the central antinodal line)?
j. Which of the labeled points are located on the third nodal line (using the notation that the third nodal line is the third nodal line directly to the left or the right of the central antinodal line)?
|
Answers: See diagram above for a visual representation of many of the answers.
a. ACDEHLMOPQ are all antinodal points which lie on antinodal lines. They are formed as a result of either a crest meeting a crest (two thick lines) or a trough meeting a trough (two thin lines). At the moment in time depicted in the diagram, point A is not a crest-crest or a trough-trough interference point. However, as time progresses and the circular waves continue their motion outwards from the source, point A (and all points on the antinodal lines) will be locations of crest-crest (or trough-trough) interference. At some instant in time, all points falling upon antinodal lines will be locations of constructive interference.
b. BFGJKNRS are all nodal points. They are formed as a result of a crest (thick line) meeting a trough (thin line).
c. CDEHLMOPQ (and possibly A) are all formed by constructive interference. They are all antinodal points and as such, they are the result of constructive interference. Point A is certainly not an antinodal point; however it is likely the result of constructive interference - two waves meeting with their displacement in the same direction (just not two crests or two troughs).
d. CL are on the central antinodal line. The central antinodal line is marked on the diagram above as AN0. It is the line which extends from the midpoint of the line connecting the two sources.
e. EHPQ are on the first antinodal line. They lie on the first antinodal line to the left or right of the central antinodal line. See diagram above.
f. ADMO are on the second antinodal line. They lie on the second antinodal line to the left or right of the central antinodal line. See diagram above.
g. There is no third antinodal line. See diagram above.
h. FG are on the first nodal line. They lie on the first nodal line to the left or right of the central antinodal line. See diagram above.
i. BKR are on the second nodal line. They lie on the second nodal line to the left or right of the central antinodal line. See diagram above.
j. JNS are on the third nodal line. They lie on the third nodal line to the left or right of the central antinodal line. See diagram above.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
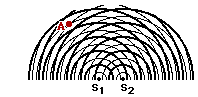 22. Consider the interference pattern at the right. (The crests are represented by thick lines and the troughs by thin lines.) If the distance from S1 to point A is 49.5 cm and the distance from S2 to point A is 60.5 cm, then what is the wavelength?
22. Consider the interference pattern at the right. (The crests are represented by thick lines and the troughs by thin lines.) If the distance from S1 to point A is 49.5 cm and the distance from S2 to point A is 60.5 cm, then what is the wavelength?
|
Answer: W = 11.0 cm
Given: S1A = 49.5 cm and S2A = 60.5 cm and m=1 (the point is on the first antinodal line to the right of center)
Find: W (wavelength)
Strategy: Find the path difference (PD) from the two distances and then use the PD = m • W equation to calculate the wavelength.
PD = | S2A - S1A | = | 60.5 cm - 49.5 cm | = 11.0 cm
Now substitute into the path difference-wavelength equation and solve for wavelength (W):
11.0 cm = 1 • W
W = 11.0 cm
An alternative strategy involves recognizing from the diagram that point A is a distance of 4.5 wavelengths from point S1. Thus, the distance 49.5 cm equals 4.5 • W. Solving for W yields 11.0 cm. The same strategy can be used for the distance from S2 to point A, yielding the same answer.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
2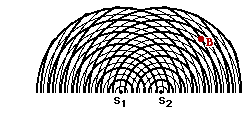 3. Consider the interference pattern at the right. (The crests are represented by thick lines and the troughs by thin lines.) If the distance from S1 to point B is 50.4 cm and the distance from S2 to point A is 34.5 cm, then what is the wavelength?
3. Consider the interference pattern at the right. (The crests are represented by thick lines and the troughs by thin lines.) If the distance from S1 to point B is 50.4 cm and the distance from S2 to point A is 34.5 cm, then what is the wavelength?
|
Answer: 6.28 cm
Given: S1B = 50.4 cm and S2B = 34.5 cm and m=2.5 (the point is on the third nodal line to the right of center)
Find: W (wavelength)
Strategy: Find the path difference (PD) from the two distances and then use the PD = m • W equation to calculate the wavelength.
PD = | S2B - S1B | = | 34.5 cm - 50.4 cm | = 15.7 cm
Now substitute into the path difference-wavelength equation and solve for wavelength (W):
15.7 cm = 2.50 • W
W = 6.28 cm
An alternative strategy involves recognizing from the diagram that point B is a distance of 8 wavelengths from point S1. Thus, the distance 50.4 cm equals 8 • W. Solving for W yields 6.28 cm. The same strategy can be used for the distance from S2 to point B, yielding the same answer.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
24. Two point sources are vibrating in phase to produce an interference pattern. The wavelength of the waves is 7.60 cm. Point C is a point on the third nodal line. The distance from S1 (the nearest source) to point C is 65.6 cm. Determine the distance from S2 to point C.
|
Answer: 84.6 cm
Given: S1C = 65.6 cm and W = 7.6 cm and m=2.5 (third nodal line)
Find: S2C
Strategy: Find the path difference (PD) using the equation PD = m • W. The path difference signifies the difference in distance from the sources to the nearest point. The S2C distance is larger than the S1C distance by an amount equal to the path difference.
First find the path difference:
PD = m • W = 2.50 • 7.60 cm = 19.0 cm
Now add the path difference to the S1C distance to determine S2C.
S2C = S1C + PD = 65.6 cm + 19.0 cm = 84.6 cm
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
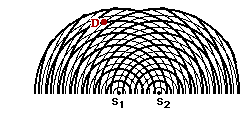 25. Consider the interference pattern at the right. (The crests are represented by thick lines and the troughs by thin lines.) The distance from S1 to point D is 47.2 cm. What is the wavelength? What is the distance from S2 to point D? (HINT: Use the diagram.)
25. Consider the interference pattern at the right. (The crests are represented by thick lines and the troughs by thin lines.) The distance from S1 to point D is 47.2 cm. What is the wavelength? What is the distance from S2 to point D? (HINT: Use the diagram.)
|
Answer: wavelength = 7.87 cm; S2D = 59.0 cm
Given: S1D = 47.2 cm and m = 1.50 (the second nodal line to the left of the central antinodal line)
Find: W and S2D
Strategy: Since neither a wavelength or a path difference is given or implicitly stated, the diagram will have to be used to determine the wavelength. The wavelength will then be used to determine the path difference and the path difference will be used to find the S2D distance.
From the diagram, it is observed that the point D is exactly 6 full wavelengths from S1. So S1D = 6.00 • W. Substituting and solving for W yields the following:
47.2 cm = 6.00 • W
W = (47.2 cm) / 6.00 = 7.87 cm
Now the path difference can be found using the relationship PD = m • W where m = 1.50 and W = 7.87 cm. Substituting and solving for PD yields
PD = m • W = 1.50 • (7.87 cm) = 11. 8 cm
This means that the point S2 is 11.8 cm further from the point D than S1's distance from point D. So adding 11.8 cm to 47.2 cm yields 59.0 cm.
|
26. Laser light is directed towards a pair of slits which are 2.50 x 10-2 mm apart. The light shines on a screen 8.20 meters away and an interference pattern is observed. A point on the 3rd antinode is observed to be 39.6 cm away from the central antinode. What is the wavelength of the laser light in units of nanometers? (1 m = 109 nm)
|
Answer: 402 nm
Given: d = 2.50 x 10-2 mm; L = 8.20 m; m = 3; y = 39.6 cm
Find: wavelength (W)
Strategy: Substitute into Young's equation and solve for W; be very careful with units - in fact, first perform conversions to get all quantities in unit of meters. Once the W is calculated, convert it to nanometers.
First the conversions of all given quantities to meters yields:
d = 2.50 x 10-5 m; L = 8.20 m; y = 0.396 m
Now substitute into Young's equation:
W = y • d / (m • L) = (0.396 m) • (2.50 x 10-5 m) / [(3) • (8.20 m)] = 4.02 x 10-7 m
Now convert to meters using the conversion factor: (1•109 nm/1 m). This yields 402 nm as the answer.
|
27. This same laser light (from #26) is reflected off of the grooves in a compact disc. The disc is 4.5 meters from the screen where its interference pattern is projected. Antinode 1 is found to be 1.2 meters from the central antinode. What is the spacing between the "grooves" of the C.D.?
|
Answer: 1.5 x 10-6 m
Given: W = 4.02 x 10-7 m; L = 4.5 m; m = 1; y = 1.2 m
Find: d
Strategy: Use Young's equation to solve for the unknown quantity.
Rearrange Young's equation to produce an equation with d expressed in terms of the known quantities.
d = m • L • W / y
Substitute and solve
d = (1) • (4.5 m) • (4.02 x 10-7 m) / (1.2 m) = 1.5 x 10-6 m
|
28. Different colors of paper are illuminated with different primary colors of light. Determine the colors of light absorbed by the paper (if any), the colors of light reflected by the paper (if any), and the appearance of the paper.
| |
Color of Light
|
Color of Paper
|
Colors Absorbed
|
Colors Reflected
|
Appearance
|
|
a.
|
White
|
White
|
None
|
RGB
|
White
|
|
b.
|
Cyan
(= GB)
|
White
|
None
|
GB
|
Cyan
|
|
c.
|
Yellow
(= RG)
|
White
|
None
|
RG
|
Yellow
|
|
d.
|
Red
|
Yellow
|
None
(B if present)
|
R
|
Red
|
|
e.
|
Red
|
Blue
|
R
(G if present)
|
None
|
Black
|
|
f.
|
Red
|
Cyan
|
R
|
None
|
Black
|
|
g.
|
Red
|
Red
|
None
(GB if present)
|
R
|
Red
|
|
h.
|
Magenta
(= RB)
|
Red
|
B
(G if present)
|
R
|
Red
|
|
i.
|
Yellow
(= RG)
|
Red
|
G
(B if present)
|
R
|
Red
|
|
j.
|
Cyan
(= GB)
|
Red
|
GB
|
None
|
Black
|
|
k.
|
Cyan
(= GB)
|
Blue
|
G
(R if present)
|
B
|
Blue
|
|
l.
|
Yellow
(= RG )
|
Blue
|
RG
|
None
|
Black
|
|
m.
|
Yellow
(= RG )
|
Green
|
R
(B if present)
|
G
|
Green
|
|
n.
|
Yellow
(= RG )
|
Cyan
|
R
|
G
|
green
|
|
o.
|
Yellow
(= RG)
|
Magenta
|
G
|
R
|
Red
|
|
Answer: See table above
In the first column, if a secondary color of light is shown, it is translated into the equivalent primaries. These primaries will strike the paper and may or may not be absorbed. The color which a paper pigment will absorb is the complementary color; this color is typically expressed in terms of the equivalent primary colors of light. The subtraction process is then done to determine what primary color of light is reflected. This/these reflected primaries determine the color appearance of the paper. They are added (if there are more than 2) to determine the resulting appearance. As an example of the entire process, consider row i:
Row i: Yellow light is equivalent to red and green (RG). Red paper contains pigments capable of absorbing both green and blue light if present. Only green light is present, so it is absorbed. So the subtraction process is
RG - G = R
Red light is reflected; this gives the paper the appearance of red.
The same process can be performed for all other parts of this question.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
Navigate to:
Review Session Home - Topic Listing
Light Waves and Color - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-#11 || #12-#20 || #21-#28
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Light Waves
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 5 of the series includes topics on Light Waves and Color.
Visit: MOP the App Home || MOP the App - Part 5