The Physics Classroom » Calculator Pad » Vectors and Projectiles » Equation Overview

Mechanics: Vectors and Projectiles

Problem Sets || Overview of Physics || Legacy Problem Set

Vectors and Projectiles: Problem Set Overview

There are 17 ready-to-use problem sets on the topic of Vectors and Projectiles. The problems target your ability to perform basic vector operations such as vector addition and vector resolution, to use right angle trigonometry and vector addition principles to analyze physical situations involving displacement vectors, and to combine a conceptual understanding of projectile motion with an ability to use kinematic equations in order to solve horizontally and non-horizontally launched projectile problems. Problems range in difficulty from the very easy and straight-forward to the very difficult and complex.

Direction: The Counter-Clockwise From East Convention

A vector is a quantity that has magnitude and direction. The direction can be described as being east, west, north, or south using the typical map convention. Most of us are familiar with the map convention for the direction of a vector. On a map, up on the page is usually in the direction of North and to the right on the page is usually in the direction of east. In Physics, we utilize the map convention to express the direction of a vector. When a vector is neither north or south or east or west, an additional convention must be used. One convention commonly used for expressing the direction of vectors is the counter-clockwise from east convention (CCW). The direction of a vector is represented as the counter-clockwise angle of rotation which the vector makes with due East. This video on the Direction of Vectors will provide much help on understanding direction conventions.

Vector Addition

Often times a motion involves several segments or legs. For instance, a person in a maze makes several individual displacements in order to finish some distance out of place from the starting position. Such individual displacement vectors can be added using a head-to-tail method of vector addition. If adding vector B to vector A, then vector A should be drawn first; then vector B should be added to it by drawing it so that the tail of vector B starts at the location where the head of vector A ends. The resultant vector is then drawn from the tail of A (starting point) to the head of B (finishing point). The resultant is equivalent to the sum of the individual vectors. In this set of problems, you will have to be able to read the word story problem and sketch an appropriate vector addition diagram. The diagram becomes an important tool in the solution of the problem. This video explains more about the Graphical Method of Vector Addition.

Adding Right Angle Vectors

Two vectors that are added at right angles to each other will sum to a resultant vector that is the hypotenuse of a right triangle. The Pythagorean theorem can be used to relate the magnitude of the hypotenuse to the magnitudes of the other two sides of the triangle. The angles within the right triangle can be determined from knowledge of the length of the sides using trigonometric functions. The mnemonic SOH CAH TOA can help one remember how the lengths of the opposite, adjacent and hypotenuse sides of the right triangle are related to the angle value. Use this video to learn more about Adding Right Angle Vectors.

Resolving an Angled Vector into Right Angle Components

If one of the vectors to be added is not directed due east, west, north or south, then vector resolution can be employed in order to simplify the addition process. Any vector which makes an angle to one of the axes can be projected onto the axes to determine its components. Trigonometric functions (remembered by SOH CAH TOA) can be used to resolve such a vector and to determine the magnitudes of its x- and y- components. By resolving an angled vector into x- and y-components, the components of the vector can be substituted for the actual vector itself and used in solving a vector addition diagram. The resolution of angled vectors into x- and y-components allows a student to determine the magnitude of the sides of the resultant vector by summing up all the east-west and north-south components. Need more help or some examples? Try the video on the Analytical Method of Vector Addition.

Relative Velocity Situations

Often times an object is moving within a medium that is moving relative to its surroundings. For instance, a plane moves through air which (due to winds) is moving relative to the land below. And a boat moves through water which (due to currents) is moving relative to the land on the shore. In such situations, an observer on land will observe the plane or the boat to move at a different velocity than an observer in the boat or the plane would observe. It's a matter of reference frame. One's perception of a motion is dependent upon one's reference frame - whether the person is in the boat, the plane or on land.

In a relative velocity problem, information is typically stated about the motion of the plane relative to the air (plane velocity) or the motion of the boat relative to the water (boat velocity). And information about the motion of the air relative to the ground (wind velocity or air velocity) or the motion of the water relative to the shore (water velocity or river velocity ) is typically stated. The problem centers around relating these two components of the plane or boat motion to the resulting velocity. The resulting velocity of the plane or boat relative to the land is simply the vector sum of the plane or boat velocity and the wind or river velocity.

The approach to such problems demands a careful reading (and re-reading) of the problem statement and a careful sketch of the physical situation. Efforts must be made to avoid mis-interpreting the physical situation. Once properly set-up, the algebraic manipulations become relatively simply and straight-forward. The crux of the problem is typically associated with the reading, interpreting and understanding of the problem statement. You can see examples in our video on Relative Velocity and River Boat Problems.

Projectile Motion

A projectile is an object upon which the only force of influence is the force of gravity. As a projectile moves through the air, its trajectory is effected by the force of gravity; air resistance is assumed to have a negligible effect upon the motion. Because gravity is the only force, the acceleration of a projectile is the acceleration caused by gravity - 9.8 m/s/s, down. As such, projectiles travel along their trajectory with a constant horizontal velocity and a changing vertical velocity. The vertical velocity changes by -9.8 m/s each second. (Here the - sign indicates that an upward velocity value would be decreasing and a downward velocity value would be increasing.)

A projectile has a motion that is both horizontal and vertical at the same time. These two independent components of motion can be described by kinematic equations. Since perpendicular components of motion are independent of each other, any motion in the horizontal direction is unaffected by a motion in a vertical direction (and vice versa). As such, two separate sets of equations are used to describe the horizontal and the vertical components of a projectile's motion. These equations are described below.

The VoxVoy Equations

Projectile problems in this set of problems can be divided into two types - those that are launched in a strictly horizontal direction and those that are launched at an angle to the horizontal. A horizontally launched projectile has an original velocity which is directed only horizontally; there is no vertical component to the original velocity. It is sometimes said that v_oy = 0 m/s for such problems. (The v_oy is the y-component of the original velocity.)

A non-horizontally launched projectile (or angled-launched projectile) is a projectile that is launched at an angle to the horizontal. Such a projectile has both a horizontal and vertical component to its original velocity. The magnitudes of the horizontal and vertical components of the original velocity can be calculated from knowledge of the original velocity and the angle of launch (theta or Θ) using trigonometric functions. The equations for such calculations are

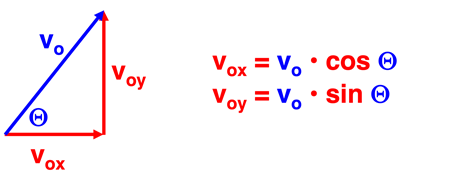
VoxVoy Equations

The quantities v_ox and v_oy are the x- and y-components of the original velocity. The values of v_ox and v_oy are related to the original velocity (v_o) and the angle of launch (Θ). Here the angle of launch is defined as the angle with respect to the horizontal. This relationship is depicted in the diagram.

Try our 8-minute video on the Mathematics of Projectile Motion for a thorough overview of the formulas and approach for solving projectile problems.

The Known and Unknown Variables

It is highly suggested that you utilize an x-y table to organize your known and unknown information. An x-y table lists kinematic quantities in terms of horizontal and vertical components of motion. The horizontal displacement, initial horizontal velocity. and horizontal acceleration are all listed in the same column. A separate column is used for the vertical components of displacement, initial velocity and acceleration. In this problem set, you will have to give attention to the following kinematic quantities and their corresponding symbols.

Given these symbols for the basic kinematic quantities, an x-y table for a projectile problem would have the following form:

Horizontal	Vertical
x = __________________ v_ox = __________________ a_x = __________________ v_fx = __________________ t = __________________	y = __________________ v_oy = __________________ a_y = __________________ v_fy = __________________ t = __________________

Known values would be inserted into the blanks.

Try our 8-minute video on the Mathematics of Projectile Motion for a thorough overview of the formulas and approach for solving projectile problems.

The Formulas

Of the nine quantities listed above, eight are vectors that have a specific direction associated with them. Time is the only quantity that is a scalar. As a scalar, time can be listed in an x-y table in either the horizontal or the vertical columns. In a sense, time is the one quantity that bridges the gap between the two columns. While horizontal and vertical components of motion are independent of each other, both types of quantities are dependent upon time. This is best illustrated when inspecting the kinematic equations that are used to solve projectile motion problems. The graphic below shows how the four 1-dimensional kinematic equations can be used to describe the horizontal and the vertical motion of a projectile. Subscripts of x (for horizontal) and y (for vertical) have been inserted after each vector quantity in the equations.

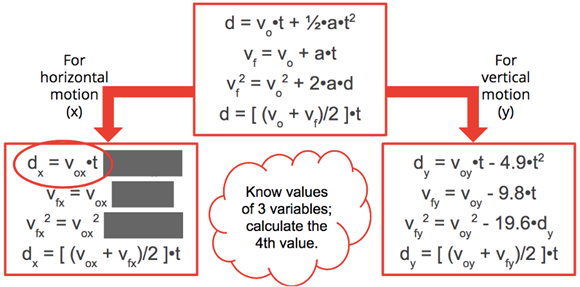
If the understanding that a projectile is an object upon which the only force is gravity is applied to these projectile situations, then it is clear that there is no horizontal acceleration. Gravity only accelerates projectiles vertically, so the horizontal acceleration is 0 m/s/s. Any term containing the a_x variable will thus cancel. There are three equations on the left side of the graphic for horizontal motion that contain the a_x variable; these have thus been greyed out. The first equation listed for horizontal motion (circled in red) is the equation that is most often used.

Try our 8-minute video on the Mathematics of Projectile Motion for a thorough overview of the formulas and approach for solving projectile problems.

Trajectory Diagram and Characteristics

Non-horizontally launched projectiles (or angle-launched projectiles) move horizontally above the ground as they move upward and downward through the air. One special case is a projectile which is launched from ground level, moves upwards towards a peak position, and subsequently falls from the peak position back to the ground. A trajectory diagram is often used to depict the motion of such a projectile. The diagram below depicts the path of the projectile and also displays the components of its velocity at regular time intervals.

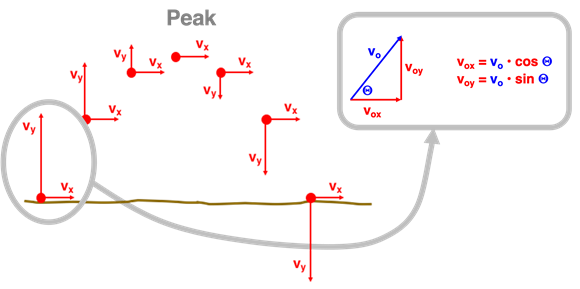
The v_x and v_y vectors in the diagram represent the horizontal and vertical components of the velocity at each instant during the trajectory. A careful inspection shows that the v_x values remain constant throughout the trajectory. The v_y values decrease as the projectile rises from its initial location towards the peak position. As the projectile falls from its peak position back to the ground, the v_y values increase. In other words, the projectile slows down as it rises upward and speeds up as it falls downward. This information is consistent with the definition of a projectile - an object whose motion is influenced solely by the force of gravity; such an object will experience a vertical acceleration only.

At least three other principles are observed in the trajectory diagram which apply to this special case of an angle-launched projectile problem.

The time for a projectile to rise to the peak is equal to the time for it to fall to the peak. (The peak, the highest point, is labeled on the diagram.) The total time (t_total) is thus the time up (t_up) to the peak multiplied by two:

t_total = 2 • t_up
At the peak of the trajectory, there is no vertical velocity for a projectile. The equation v_fy = v_oy + a_y • t can be applied to the first half of the trajectory of the projectile. In such a case, t represents t_up and the v_fy at this instant in time is 0 m/s. By substituting and re-arranging, the following derivation is performed.

v_fy = v_oy + ay • t

0 m/s = v_oy + (-9.8 m/s/s) • t_up

t_up = v_oy / (9.8 m/s/s)
The projectile strikes the ground with a vertical velocity that is equal in magnitude to the vertical velocity with which it left the ground. That is,

v_fy = v_oy

Try our 8-minute video on the Mathematics of Projectile Motion for a thorough overview of the formulas, concepts, and approach for solving projectile problems.

The Basic Strategy

The basic approach to solving projectile problems involves reading the problem carefully and visualizing the physical situation. A well-constructed diagram is often a useful means of visualizing the situation. Then list and organize all known and unknown information in terms of the symbols used in the projectile motion equations. An x-y table is a useful organizing scheme for listing such information. Inspect all known quantities, looking for either three pieces of horizontal information or three pieces of vertical information. Since all kinematic equations list four variables, knowledge of three variables allows you to determine the value of a fourth variable. For instance, if three pieces of vertical information are known, then the vertical equations can be used to determine a fourth (and a fifth) piece of vertical information. Often times, the fourth piece of information is the time. In such instances, the time can then be combined with two pieces of horizontal information to calculate another horizontal variable using the ...

Try our 8-minute video on the Mathematics of Projectile Motion for a thorough overview of the formulas, concepts, and approach for solving projectile problems.

Habits of an Effective Problem-Solver

An effective problem solver by habit approaches a physics problem in a manner that reflects a collection of disciplined habits. While not every effective problem solver employs the same approach, they all have habits that they share in common. These habits are described briefly here. An effective problem-solver...

...reads the problem carefully and develops a mental picture of the physical situation. If needed, they sketch a simple diagram of the physical situation to help visualize it.
...identifies the known and unknown quantities in an organized manner, often times recording them on the diagram itself. They equate given values to the symbols used to represent the corresponding quantity (e.g., v_ox = 12.4 m/s, v_oy = 0.0 m/s, d_x = 32.7 m, d_y = ???).
...plots a strategy for solving for the unknown quantity; the strategy will typically centers around the use of physics equations and is heavily dependent upon an understanding of physics principles.
...identifies the appropriate formula(s) to use, often times writing them down. Where needed, they perform the needed conversion of quantities into the proper unit.
...performs substitutions and algebraic manipulations in order to solve for the unknown quantity.

Additional Readings/Study Aids:

The following pages from The Physics Classroom tutorial may serve to be useful in assisting you in the understanding of the concepts and mathematics associated with these problems.

Watch a Video

We have developed and continue to develop Video Tutorials on introductory physics topics. You can find these videos on our YouTube channel. We have an entire Playlist on the topic of Vectors and Projectiles.