Mechanics: Work, Energy and Power
Calculator Pad, Version 2
You are viewing the Legacy Version of The Calculator Pad. We have recently revised and improved The Calculator Pad.
Version 2 is now LIVE! We have more than tripled the number of problems, broken each unit into several smaller, single-topic problem sets, and utilized a random number generator to provide numerical information for each problem. Student answers are automatically evaluated and feedback is instant. And we've maintained the same commitment to providing help via links to existing resources. While the FREE version does all the above, teachers with a Task Tracker subscription can take things a step further. They can modify our pre-made problem sets, write their own problems with our easy-to-use Problem Builder, and use the Calculator Pad to design their own program that expresses their emphasis on the use of mathematics in Physics.
Return to the
Main Page to link into Version 2. Learn more
About Version 2. Or visit the
Store to make a Task Tracker purchase.
Work, Energy and Power: Problem Set
Problem 1:
Renatta Gass is out with her friends. Misfortune occurs and Renatta and her friends find themselves getting a workout. They apply a cumulative force of 1080 N to push the car 218 m to the nearest fuel station. Determine the work done on the car.
Problem 2:
Hans Full is pulling on a rope to drag his backpack to school across the ice. He pulls upwards and rightwards with a force of 22.9 Newtons at an angle of 35 degrees above the horizontal to drag his backpack a horizontal distance of 129 meters to the right. Determine the work (in Joules) done upon the backpack.
Problem 3:
Lamar Gant, U.S. powerlifting star, became the first man to deadlift five times his own body weight in 1985. Deadlifting involves raising a loaded barbell from the floor to a position above the head with outstretched arms. Determine the work done by Lamar in deadlifting 300 kg to a height of 0.90 m above the ground.
Problem 4:
Sheila has just arrived at the airport and is dragging her suitcase to the luggage check-in desk. She pulls on the strap with a force of 190 N at an angle of 35° to the horizontal to displace it 45 m to the desk. Determine the work done by Sheila on the suitcase.
Problem 5:
While training for breeding season, a 380 gram male squirrel does 32 pushups in a minute, displacing its center of mass by a distance of 8.5 cm for each pushup. Determine the total work done on the squirrel while moving upward (32 times).
Problem 6:
During the Powerhouse lab, Jerome runs up the stairs, elevating his 102 kg body a vertical distance of 2.29 meters in a time of 1.32 seconds at a constant speed.
a. Determine the work done by Jerome in climbing the stair case.
b. Determine the power generated by Jerome.
Problem 7:
A new conveyor system at the local packaging plan will utilize a motor-powered mechanical arm to exert an average force of 890 N to push large crates a distance of 12 meters in 22 seconds. Determine the power output required of such a motor.
Problem 8:
The Taipei 101 in Taiwan is a 1667-foot tall, 101-story skyscraper. The skyscraper is the home of the world’s fastest elevator. The elevators transport visitors from the ground floor to the Observation Deck on the 89th floor at speeds up to 16.8 m/s. Determine the power delivered by the motor to lift the 10 passengers at this speed. The combined mass of the passengers and cabin is 1250 kg.
Problem 9:
The ski slopes at Bluebird Mountain make use of tow ropes to transport snowboarders and skiers to the summit of the hill. One of the tow ropes is powered by a 22-kW motor which pulls skiers along an icy incline of 14° at a constant speed. Suppose that 18 skiers with an average mass of 48 kg hold onto the rope and suppose that the motor operates at full power.
a. Determine the cumulative weight of all these skiers.
b. Determine the force required to pull this amount of weight up a 14° incline at a constant speed.
c. Determine the speed at which the skiers will ascend the hill.
Problem 10:
The first asteroid to be discovered is Ceres. It is the largest and most massive asteroid is our solar system’s asteroid belt, having an estimated mass of 3.0 x 1021 kg and an orbital speed of 17900 m/s. Determine the amount of kinetic energy possessed by Ceres.
Problem 11:
A bicycle has a kinetic energy of 124 J. What kinetic energy would the bicycle have if it had …
a. … twice the mass and was moving at the same speed?
b. … the same mass and was moving with twice the speed?
c. … one-half the mass and was moving with twice the speed?
d. … the same mass and was moving with one-half the speed?
e. … three times the mass and was moving with one-half the speed?
Problem 12:
A 78-kg skydiver has a speed of 62 m/s at an altitude of 870 m above the ground.
a. Determine the kinetic energy possessed by the skydiver.
b. Determine the potential energy possessed by the skydiver.
c. Determine the total mechanical energy possessed by the skydiver.
Problem 13:
Lee Ben Fardest (esteemed American ski jumper), has a mass of 59.6 kg. He is moving with a speed of 23.4 m/s at a height of 44.6 meters above the ground. Determine the total mechanical energy of Lee Ben Fardest.
Problem 14:
Chloe leads South’s varsity softball team in hitting. In a game against New Greer Academy this past weekend, Chloe slugged the 181-gram softball so hard that it cleared the outfield fence and landed on Lake Avenue. At one point in its trajectory, the ball was 28.8 m above the ground and moving with a speed of 19.7 m/s. Determine the total mechanical energy of the softball.
Problem 15:
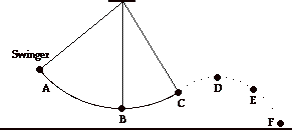
Olive Udadi is at the park with her father. The 26-kg Olive is on a swing following the path as shown. Olive has a speed of 0 m/s at position A and is a height of 3.0-m above the ground. At position B, Olive is 1.2 m above the ground. At position C (2.2 m above the ground), Olive projects from the seat and travels as a projectile along the path shown. At point F, Olive is a mere picometer above the ground. Assume negligible air resistance throughout the motion. Use this information to fill in the table.
| Position |
Height (m) |
PE (J) |
KE (J) |
TME (J) |
Speed (m/s) |
| A |
3.0 |
|
|
|
0.0 |
| B |
1.2 |
|
|
|
|
| C |
2.2 |
|
|
|
|
| F |
0 |
|
|
|
|
Problem 16:
Suzie Lavtaski (m=56 kg) is skiing at Bluebird Mountain. She is moving at 16 m/s across the crest of a ski hill located 34 m above ground level at the end of the run.
a. Determine Suzie's kinetic energy.
b. Determine Suzie's potential energy relative to the height of the ground at the end of the run.
c. Determine Suzie's total mechanical energy at the crest of the hill.
d. If no energy is lost or gained between the top of the hill and her initial arrival at the end of the run, then what will be Suzie's total mechanical energy at the end of the run?
e. Determine Suzie's speed as she arrives at the end of the run and prior to braking to a stop.
Problem 17:
Nicholas is at The Noah's Ark Amusement Park and preparing to ride on The Point of No Return racing slide. At the top of the slide, Nicholas (m=72.6 kg) is 28.5 m above the ground.
a. Determine Nicholas' potential energy at the top of the slide.
b. Determine Nicholas's kinetic energy at the top of the slide.
c. Assuming negligible losses of energy between the top of the slide and his approach to the bottom of the slide (h=0 m), determine Nicholas's total mechanical energy as he arrives at the bottom of the slide.
d. Determine Nicholas' potential energy as he arrives at the bottom of the slide.
e. Determine Nicholas' kinetic energy as he arrives at the bottom of the slide.
f. Determine Nicholas' speed as he arrives at the bottom of the slide.
Problem 18:
Ima Scaarred (m=56.2 kg) is traveling at a speed of 12.8 m/s at the top of a 19.5-m high roller coaster loop.
a. Determine Ima's kinetic energy at the top of the loop.
b. Determine Ima's potential energy at the top of the loop.
c. Assuming negligible losses of energy due to friction and air resistance, determine Ima's total mechanical energy at the bottom of the loop (h=0 m).
d. Determine Ima's speed at the bottom of the loop.
Problem 19:
Justin Thyme is traveling down Lake Avenue at 32.8 m/s in his 1510-kg 1992 Camaro. He spots a police car with a radar gun and quickly slows down to a legal speed of 20.1 m/s.
a. Determine the initial kinetic energy of the Camaro.
b. Determine the kinetic energy of the Camaro after slowing down.
c. Determine the amount of work done on the Camaro during the deceleration.
Problem 20:
Pete Zaria works on weekends at Barnaby's Pizza Parlor. His primary responsibility is to fill drink orders for customers. He fills a pitcher full of Cola, places it on the counter top and gives the 2.6-kg pitcher a 8.8 N forward push over a distance of 48 cm to send it to a customer at the end of the counter. The coefficient of friction between the pitcher and the counter top is 0.28.
a. Determine the work done by Pete on the pitcher during the 48 cm push.
b. Determine the work done by friction upon the pitcher .
c. Determine the total work done upon the pitcher .
d. Determine the kinetic energy of the pitcher when Pete is done pushing it.
e. Determine the speed of the pitcher when Pete is done pushing it.
Problem 21:
The Top Thrill Dragster stratacoaster at Cedar Point Amusement Park in Ohio uses a hydraulic launching system to accelerate riders from 0 to 53.6 m/s (120 mi/hr) in 3.8 seconds before climbing a completely vertical 420-foot hill.
a. Jerome (m=102 kg) visits the park with his church youth group. He boards his car, straps himself in and prepares for the thrill of the day. What is Jerome's kinetic energy before the acceleration period?
b. The 3.8-second acceleration period begins to accelerate Jerome along the level track. What is Jerome's kinetic energy at the end of this acceleration period?
c. Once the launch is over, Jerome begins screaming up the 420-foot, completely vertical section of the track. Determine Jerome's potential energy at the top of the vertical section. (GIVEN: 1.00 m = 3.28 ft)
d. Determine Jerome's kinetic energy at the top of the vertical section.
e. Determine Jerome's speed at the top of the vertical section.
Problem 22:
Paige is the tallest player on South's Varsity volleyball team. She is in spiking position when Julia gives her the perfect set. The 0.226-kg volleyball is 2.29 m above the ground and has a speed of 1.06 m/s. Paige spikes the ball, doing 9.89 J of work on it.
a. Determine the potential energy of the ball before Paige spikes it.
b. Determine the kinetic energy of the ball before Paige spikes it.
c. Determine the total mechanical energy of the ball before Paige spikes it.
d. Determine the total mechanical energy of the ball upon hitting the floor on the opponent's side of the net.
e. Determine the speed of the ball upon hitting the floor on the opponent's side of the net.
Problem 23:
According to ABC's Wide World of Sports show, there is the thrill of victory and the agony of defeat. On March 21 of 1970, Vinko Bogataj was the Yugoslavian entrant into the World Championships held in former West Germany. By his third and final jump of the day, heavy and persistent snow produced dangerous conditions along the slope. Midway through the run, Bogataj recognized the danger and attempted to make adjustments in order to terminate his jump. Instead, he lost his balanced and tumbled and flipped off the slope into the dense crowd. For nearly 30 years thereafter, footage of the event was included in the introduction of ABC's infamous sports show and Vinco has become known as the agony of defeat icon.
a. Determine the speed of 72-kg Vinco after skiing down the hill to a height which is 49 m below the starting location.
b. After descending the 49 m, Vinko tumbled off the track and descended another 15 m down the ski hill before finally stopping. Determine the change in potential energy of Vinko from the top of the hill to the point at which he stops.
c. Determine the amount of cumulative work done upon Vinko's body as he crashes to a halt.
Problem 24:
Nolan Ryan reportedly had the fastest pitch in baseball, clocked at 100.9 mi/hr (45.0 m/s) If such a pitch had been directed vertically upwards at this same speed, then to what height would it have traveled?
Problem 25:
In the Incline Energy lab, partners Anna Litical and Noah Formula give a 1.00-kg cart an initial speed of 2.35 m/s from a height of 0.125 m above the lab table. Determine the speed of the cart when it is located 0.340 m above the lab table.
Problem 26:
In April of 1976, Chicago Cub slugger Dave Kingman hit a home run which cleared the Wrigley Field fence and hit a house located 530 feet (162 m) from home plate. Suppose that the 0.145-kg baseball left Kingman's bat at 92.7 m/s and that it lost 10% of its original energy on its flight through the air. Determine the speed of the ball when it cleared the stadium wall at a height of 25.6 m.
Problem 27:
Dizzy is speeding along at 22.8 m/s as she approaches the level section of track near the loading dock of the Whizzer roller coaster ride. A braking system abruptly brings the 328-kg car (rider mass included) to a speed of 2.9 m/s over a distance of 5.55 meters. Determine the braking force applied to Dizzy's car.
Problem 28:
A 6.8-kg toboggan is kicked on a frozen pond, such that it acquires a speed of 1.9 m/s. The coefficient of friction between the pond and the toboggan is 0.13. Determine the distance which the toboggan slides before coming to rest.
Problem 29:
Connor (m=76.0 kg) is competing in the state diving championship. He leaves the springboard from a height of 3.00 m above the water surface with a speed of 5.94 m/s in the upward direction.
a. Determine Connor's speed when he strikes the water.
b. Connor's body plunges to a depth of 2.15 m below the water surface before stopping. Determine the average force of water resistance experienced by his body.
Problem 30:
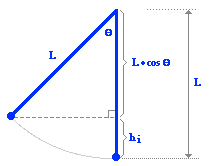
Gwen is baby-sitting for the Parker family. She takes 3-year old Allison to the neighborhood park and places her in the seat of the children's swing. Gwen pulls the 1.8-m long chain back to make a 26° angle with the vertical and lets 14-kg Allison (swing mass included) go. Assuming negligible friction and air resistance, determine Allison's speed at the lowest point in the trajectory.
Problem 31:
Sheila (m=56.8 kg) is in her saucer sled moving at 12.6 m/s at the bottom of the sledding hill near Bluebird Lake. She approaches a long embankment inclined upward at 16° above the horizontal. As she slides up the embankment, she encounters a coefficient of friction of 0.128. Determine the height to which she will travel before coming to rest.
Problem 32:
Matthew starts from rest on top of 8.45 m high sledding hill. He slides down the 32-degree incline and across the plateau at its base. The coefficient of friction between the sled and snow is 0.128 for both the hill and the plateau. Matthew and the sled have a combined mass of 27.5 kg. Determine the distance which Matthew will slide along the level surface before coming to a complete stop.
Return to Overview
View Audio Guided Solution for Problem:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32