Lesson 2: Concentration

Part d: Solution Stoichiometry

Part a: Molarity
Part b: Dilution
Part c: Percent by Mass and by Volume
Part d: Solution Stoichiometry

 

 

Determining the Moles of Solute

The concept of molarity or molar concentration was introduced in Lesson 2a. Molarity is the ratio of the moles of solute to the liters of solution. Its units are mol/L, abbreviated as M.
 
For aqueous solutions, the solute is dissolved in water. As we have seen numerous times, aqueous-state substances are often involved in chemical reactions. We know from the Stoichiometry chapter that the mathematical analysis of reactions is based on the ratio by which moles of reactants and products are involved in the reaction. For aqueous state reactants, the moles of the reactant can be determined from the volume and molarity of the solution. We learned in Lesson 2a that

Moles of solute = Volume of solute • Molarity of solute

 

When using the factor label method, the molarity is utilized as a conversion factor for converting from volume of solution to the moles of the solute. For instance, the moles of NaCl present in 250.0 mL of 0.500 M NaCl(aq) is calculated as follows:

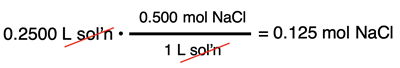
In Lesson 2d, we will revisit the topic of stoichiometry and learn how to incorporate molarity into the stoichiometric calculations for aqueous state reactants and products.
 
 
 

Stoichiometry Revisited

We introduced the topic of Stoichiometry in Chapter 9 of our Chemistry Tutorial. Stoichiometry will be a sub-topic of nearly every Chapter for the remainder of our Tutorial. Why? Because stoichiometry pertains to the quantitative nature of chemical reactions and chemical reactions is central part of what Chemistry is all about.
 
Stoichiometry is the study of the quantitative relationship between the amounts of reactants and products involved in a chemical reaction. It focuses on the How much? questions of chemical reactions. Those How much? questions require a student to relate the amount of reactants to the amount of products. In Chapter 9, those amounts, or How much? quantities, included …

1. moles of a reactant
2. moles of a product
3. mass of a reactant (in grams)
4. mass of a product (in grams)

 
In this chapter, we can add
 
5.   volume and molarity of a reactant (for aqueous-state reactants)
6.   volume and molarity of a product (for aqueous-state products)
 
to the list of How much? quantities.
 
The task of solving a stoichiometry problem requires an understanding of what is related to what? and how are they related?
 
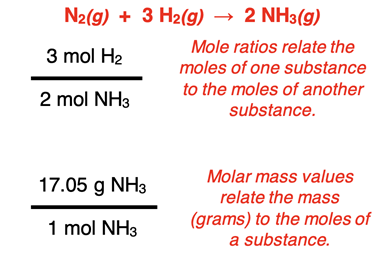
In Chapter 9, success at stoichiometry required an understanding and ability to use mole ratios and molar mass as conversion factors. A molar mass value relates the grams to the moles for any substance involved in the reaction. And the mole ratios (i.e., coefficients of the balanced chemical equation) relate the moles of one substance to the moles of a different substance involved in the reaction. Mole ratios and molar mass values provide the answers to what is related to what? type questions.
 
Coefficients (mole ratios), molar mass values, and the factor label method are the tools used to answer the how much? questions of stoichiometry. Their use was demonstrated through numerous examples in Chapter 9. If you find yourself a bit rusty on the topic, we encourage you to make a return visit to Chapter 9 and tool up.
 
   
 

Incorporating a New Conversion Pathway

The component of stoichiometry that we are adding in this chapter is the moles-molarity-volume relationship. As discussed above, molarity is a ratio that can be used as a conversion factor for converting between the liters of an aqueous solution and the moles of solute in that solution. The graphic organizer below illustrates how our new Chapter 13 relationship fits into our existing stoichiometry understanding. The boxes represent the how much? quantities. The arrows represent a conversion between those quantities. Conversion factors that are suitable for each conversion are shown next to the arrows. (MM = molar mass; M = molarity; X and Y are coefficients)
   
As we have seen in previous chapters, many problems will involve multiple steps. For instance, a problem may provide information about the molarity and volume of the aqueous solution of a reactant and ask you to determine the mass of one of the products. To use the graphic organizer to guide your factor label solution, identify the starting location (given information) on the diagram and the final destination (quantity to be determined). The arrows connecting the starting location to the final destination will guide your conversion. The number of conversion steps, the nature of each step, and the factor label used in each step are indicated on the graphic organizer. An example is shown below.
   
 
 
In the examples that follow, we will use the graphic organizer as we plan out the solution to each problem. Once the solution is planned, we will set up conversion factors with units (no numbers) in order to cancel the unit of the given quantity and acquire the unit of the desired quantity. Then we will place numbers in the numerators and denominators of our conversion factors. Finally, we will use our calculator to determine the numerical answer. This sequence of steps – Plan, Units, Numbers, Calculations – is an effective sequence for any Chemistry student wishing to master stoichiometry.
   

Example 1 - A Precipitation Reaction

Aqueous solutions of ammonium hydroxide and copper(II) chloride react to form a copper(II) hydroxide precipitate. The molecular equation is:
   
What mass of copper(II) hydroxide is produced by the reaction of 50.0 mL of a 0.500 M solution of NH₄OH with excess copper(II) chloride?
 
 

Solution

We are given the volume and molarity of a reactant and asked to determine the mass of a product.
 
Given: 50.0 mL NH₄OH(aq) solution, [NH₄OH] = 0.500 M
Determine: grams Cu(OH)₂
 
Using our graphic organizer to plan our solution, we recognize that there will be three conversion steps involved. The conversion pathway is represented by the blue arrows on the graphic.
   
The conversions involve:

1. Volume NH₄OH(aq) solution to moles NH₄OH using molarity
2. Moles NH₄OH to moles Cu(OH)₂ using the mole ratio (coefficients)
3. Moles Cu(OH)₂ to grams Cu(OH)₂ using the molar mass

 
As is our usual custom, we will string the three conversion factors together into a single 3-factor conversion. The molar mass of Cu(OH)₂ is 97.561 g/mol. This will be used in our third conversion step. We will begin by setting up the conversion factors with units (no numbers) to ensure that we are cancelling units.
 

 
Observe how the units are cancelling. A unit in the numerator or on the given quantity will be cancelled by the identical unit in a denominator of another conversion factor. The unit that does not get cancelled is the unit on our answer.
 
Setting up the problem appropriately with units guides you as you decide where to put the numbers. There is no need to memorize when to divide or multiply by a molarity. You simply need to know how the numbers and units are related. The first conversion factor involves a molarity. Since the molarity is 0.500 mol/L, the 0.500 will be placed in the numerator with the moles. A 1 will be placed in the denominator with L solution. The second conversion factor involves a mole ratio (coefficients). Since there is coefficient of 2 in front of NH₄OH in the balanced chemical equation, a 2 will be placed in the denominator with mole NH₄OH. The coefficient in front of Cu(OH)₂ is a 1; this 1 will be placed in the numerator with mol Cu(OH)₂. The third conversion factor is a molar mass. Molar mass is defined as the mass in grams per 1 mole of the substance. So, a 1 goes with mol Cu(OH)₂. The 97.561 goes with g Cu(OH)₂.
   
Insert the numbers in the appropriate locations. Then retrieve your calculator. Multiply the number of the given quantity (0.0500) by all the numbers in the numerators and divide by all the numbers in the denominators. The result - 122 g Cu(OH)₂ - is your answer.
 
 
 

Example 2 - Relating the Volume of Two Reactants

Aqueous solutions of calcium chloride and sodium phosphate are added to a flask. A precipitate is formed. The molecular equation for the reaction is:
   
What volume of 0.250 M Na₃PO₄(aq) will react completely with 100.0 mL of 0.500 M  CaCl₂(aq)? 
 
 

Solution

This problem is different than Example 1 in that it focuses on the relationship between two reactant amounts. We are given the molarities of both reactants and the volume one reactant. We are asked to determine the volume of the second reactant.
 
Given: 100.0 mL CaCl₂(aq) solution, [CaCl₂] = 0.500 M, [Na₃PO₄] = 0.250 M,
Determine: volume of Na₃PO₄(aq).  
 
We have made a slight modification of our graphic organizer to reflect that the problem focuses on the two reactants. We have noted the starting point and the final destination on the graphic.
   
The conversion pathway is indicated by the blue arrows. There will be three conversions involved. They are:

1. Volume CaCl₂(aq) solution to moles CaCl₂ using molarity of CaCl₂
2. Moles CaCl₂ to moles Na₃PO₄ using the mole ratio (coefficients)
3. Moles Na₃PO₄ to volume Na₃PO₄ using the molarity of Na₃PO₄

 
We will string the three conversion factors together into a single 3-factor conversion. We will begin by setting up the conversion factors with units (no numbers) to ensure that we are cancelling units.
   
Observe how the units cancel. The unit that does not get cancelled (L of Na₃PO₄ solution) is the unit on our answer.
 
Once satisfied with the set-up of the conversion factors, numbers are substituted into the conversion factors. There are two molarities (first and third conversion factor) and a mole ratio (coefficients).
   
Finally, our calculator is used to compute the final answer. It is 0.133 L or 133 mL. (We have rounded to the third significant digit.)
 
 
 
 

Example 3 – Solid Reactant + Solution

Rust stains (Fe₂O₃) can be removed by washing a surface with a dilute solution of oxalic acid (H₂C₂O₄). This Chemistry for Better Living hint is based by the following balanced chemical equation:
   
What volume of a 0.500 M oxalic acid is needed to remove 0.450 g of rust from a shirt? 
 
 

Solution

In the planning stage of the problem, we identify what we know – mass of the solid reactant (Fe₂O₃) and molarity of the aqueous state reactant (H₂C₂O₄). We also identify what we wish to determine (volume of H₂C₂O₄ solution). On the graphic organizer, the starting point is the mass of Fe₂O₃ and the final destination is the volume of H₂C₂O₄. The blue arrows between the starting point and the final destination represent the conversion pathway.
   
There are three conversion steps in the pathway from the starting point to the destination. The conversions involve:
 

1. Mass Fe₂O₃ to moles Fe₂O₃ using molar mass of Fe₂O₃
2. Moles Fe₂O₃ to moles H₂C₂O₄ using the mole ratio (coefficients)
3. Moles H₂C₂O₄ to volume H₂C₂O₄(aq) using molarity of H₂C₂O₄

 
The molar mass of Fe₂O₃ (from a Periodic Table) is 159.69 g/mol; this will be used in the first conversion factor.
 
We begin by setting up the conversion factors. This means we focus on units and postpone the entry of the numbers. The numbers will always follow the units into the right location (numerator or denominator) of the set up.
   
All units cancel except for the Liters of solution. This is the unit on our answer. Once satisfied with the factor label set up, we insert the numbers for the molar mass (from a Periodic Table), the mole ratio (coefficients from the balanced chemical equation), and the molarity (given in the problem statement). This is shown below.
   
The numerical answer to this problem is the result of multiplying the numerical value of the given quantity by all the numerators and dividing by all the denominators. The final answer – 0.0338 L or 33.8 mL – has been rounded to the third significant digit.
 
 
 
 

Some Final Words

Our solutions to the above examples relied on the PUNC approach. This order is extremely important. Our observation is that the most frequent student frustrations with stoichiometry occur when the early steps are skipped and students rush to their calculator without planning and setting up the solution. The calculator part should be easy. If you are finding it difficult, stalling in the midst of using it, or impulsively tapping number and operator buttons in hopes of hitting the jackpot, then you’re probably skipping the first two or three steps of P-U-N-C.
 
Finally, stoichiometry is a skill that is acquired through practice. It helps to see some worked out examples like the those above. We provided several additional problems in our Check Your Understanding section; these also have thorough solutions. BUT watching someone else generate a solution to a problem is inferior to generating you own solution to a problem. You do not want the first time that you own a solution to be on test day. So, take advantage of the opportunities described in our Before You Leave section to acquire the skill of solving solution stoichiometry problems.
 
 
 
 
 

Before You Leave

• Download our Study Card on Solution Stoichiometry. Save it to a safe location and use it as a review tool. (Coming Soon.)
• When it comes to solving Chemistry problems, our Calculator Pad is an awesome location for perfecting your skills. Try any one of the following sets of problems to level up you solution stoichiometry skills: Solution Stoichiometry 1 || Solution Stoichiometry 2 || Solution Stoichiometry 3
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.

 
 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. Example 1 was based on this reaction:
   
Suppose several trials are performed with varying amounts of NH₄OH(aq) solution having varying concentrations. Express your understanding of the relationships by filling in the blanks of the table below. Use 97.6 as the molar mass of Cu(OH)₂.
   
 
 
 
 
2. Substances AB and CD2 react according to the following double displacement reaction.
   
The molar mass of CB₂ is 38.0 g/mol.
 
a. Determine the moles of AB that react with 2.00 L of a 1.50 M solution of CD₂. 



b. Determine the mass of CB₂ produced by the reaction of a 0.500 L solution of 1.50 M of AB. 

 

 

3. Aqueous solutions of silver nitrate and potassium chloride react to form a white precipitate - AgCl. The molecular equation is …
   
What volume of 0.150 M KCl(aq) is required to completely react with 18.0 mL of 0.200 M AgNO₃(aq) ?
 


 
 
4. A Limiting Reactant Problem:
Mrs. Haber's class is performing a lab in which aqueous solutions of lead(II) nitrate and potassium iodide react to produce a lead(II) iodide precipitate. The molecular equation is
   
Antwon and Rosetta use 25.0 mL of 0.100 M Pb(NO₃)₂ and 30.0 mL of 0.150 M KI(aq).

1. How many moles of Pb(NO₃)₂ are available in their trial?
2. How many moles of KI are available in their trial?
3. Which is the limiting reactant and why?
4. What mass of lead(II) iodide will precipitate in this trial?