Lesson 2: Concentration

Part b: Dilution

Part a: Molarity
Part b: Dilution
Part c: Percent by Mass and by Volume
Part d: Solution Stoichiometry

 

What is Dilution?

Aqueous solutions are typically stored in Chemistry labs as relatively concentrated solutions known as stock solutions. When a solution is needed for any given reason, it is often made from the stock solution. A portion of the stock solution is retrieved and then diluted by adding water. The act of reducing the concentration of a solution by adding additional solvent is known as dilution.
 
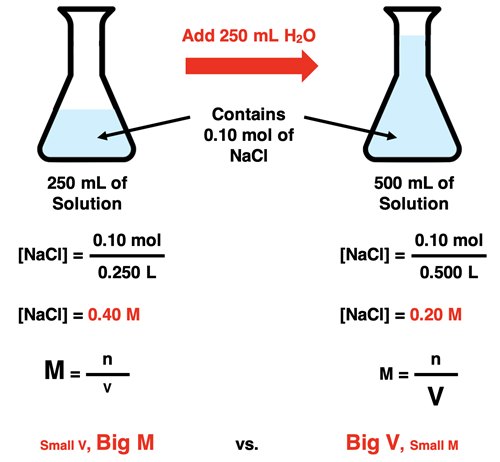
Dilution involves adding additional solvent to a sample of a solution. The process does not involve a change in the amount of solute. It is the volume of the solution that changes. Because the number of moles remains constant while the volume of the solution increases, the molarity decreases. 

 

 

A Dilution Example

A lab activity involves diluting a 1.50 M stock solution of Na₂SO₄(aq) in an effort to prepare a more dilute Na₂SO₄(aq) solution. Students are instructed to pipet 20.0 mL of the stock solution into a 100.0-mL volumetric flask. Once the stock solution has been transferred to the flask, students are to add water, mix, and then fill the flask to the 100.0 mL mark by adding more water.

 
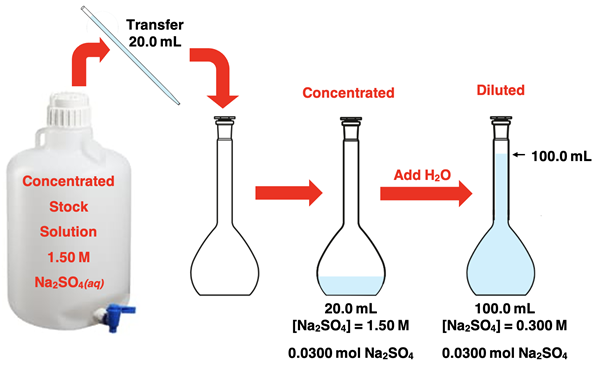
Before the dilution begins, the students have 0.0200 L of 1.50 M Na₂SO₄(aq).  The solute is Na₂SO₄. The number of moles of Na₂SO₄ initially present is 0.0300 moles:

 
The process involved adding water to the original sample. There was no change in the amount of Na₂SO₄. There was only a change in the volume of the solution from 20.0 mL (0.0200 L) to 100.0 mL (0.1000 L). When the dilution is complete, the solution contains 0.0300 mol Na₂SO₄ in 0.1000 L of solution. The final molarity is …

 

 

The Dilution Equation

The BIG principle behind dilution is that the process does not change the number of moles of solute. The number of moles of solute in the initial solution (e.g., the sample of stock solution that will be diluted) is equal to the number of moles in the final solution (the diluted solution).

Initial # of moles of solute = Final # of moles of solute

 

We learned in Lesson 2a that the moles of solute can be determined by multiplying the molarity of the solution (M) by the volume of the solution (V). That is,

# of moles of solute = M • V

When we put these two ideas together, we can generate a dilution equation that relates the volumes and molarities of the concentrated solution and the diluted solution:

M_initial • V_initial  =  M_final • V_final

where M_initial and V_initial are the molarity and volume of the original solution (before dilution) and M_final and V_final are the molarity and volume of the diluted solution. Knowing the values of any three of the four variables in the equation allows one to calculate the value of the fourth variable. The use of this equation and other dilution principles are illustrated in the following three examples.
 
 
 

Example 1

Jill Lushian is doing a chemistry lab. She has a 50.0-mL sample of iron(II) chloride with a concentration of 0.822 M.

1. How many moles of iron(II) chloride are in this solution? 
2. Jill then adds 200.0 mL of water to this solution until its final volume is 250.0 mL How many moles of iron(II) chloride are now in this solution?
3. What is the molarity of the iron(II) chloride in this final solution?

 

Solution

This three-part problem emphasizes the big principle of dilution – the number of moles of solute is not changed by diluting a solution. In part a, the moles of FeCl₂ are calculated:
 
a. # of moles FeCl₂ = (0.0500 L) • (0.822 mol FeCl₂ / 1 L) = 0.0411 mol FeCl₂
 
The part a calculation is simply the left side of the dilution equation - M_initial • V_initial. In part b, you will need to determine the number of moles in the final solution. The number of moles of solute in the diluted solution equals the initial moles of solute (from part a).
 
b. # of moles FeCl₂ = 0.0411 mol FeCl₂
 
In part c, the molarity of FeCl₂ is calculated using the molarity equation from Lesson 2a. Molarity is the moles of solute divided by the volume of solution in liters.
 
c. [FeCl₂] = moles of FeCl₂ / volume of solution = (0.0411 mol) / (0.2500 L) = 0.164 M
(The answer has been rounded to three significant digits.)
 
 

Example 2

On Day 1 of a multi-day lab, partners Ray Ahn and Polly Ester prepare a 2.10 M aqueous solution of NaOH. On Day 2, Ray and Polly take 10.0 mL of this stock solution and dilute it with water in a 125.0-mL volumetric flask.

1. How many moles of NaOH did Ray and Polly withdraw from the stock solution?
2. What is the final molar concentration of this Day 2 solution?

 

Solution

Similar to the first example, this two part problem emphasizes the big principle that the number of moles of solute does not change during the dilution process. In part a, we calculate the number of moles in the initial solution -  - M_initial • V_initial.
 
a. # of moles NaOH = (0.0100 L) • (2.10 mol NaOH / 1 L) = 0.0210 mol NaOH
 
In Part b, the molarity of NaOH is calculated using the molarity equation from Lesson 2a. Molarity is the moles of solute divided by the volume of solution in liters. The number of moles in the final solution equals the number of moles in the initial solution (calculated in Part a).
 
b. [NaOH] = moles of NaOH / volume of solution = (0.0210 mol) / (0.1250 L) = 0.168 M
 
 
 

Example 3

Jackson and Jillian have been given instructions by Mr. Tooker to make a 75.0 mL solution of 0.600 M NaCl by diluting a 3.00 M stock solution. What volume of stock solution (in mL) should they use in the process of preparing this final solution?
 
 

Solution

This is a one-part problem in which three of the four quantities in the dilution equation are given:
M_initial = 3.00 M
M_final = 0.600 M
V_final = 0.075 L
 
The goal is to determine the value of the fourth variable – the initial volume of the solution (V_initial).
V_initial = ???
 
The titration equation can be used to solve for V_initial. Begin by substituting known values into the equation.
   
To solve for V_initial, divide both sides of the equation through by 3.00 M. This isolates V_initial by itself on one side of the equation and results in …
   
Now evaluate the right side of the equation to determine the answer:
   
 
 
 

Before You Leave

• Download our Study Card on Dilution. Save it to a safe location and use it as a review tool. (Coming soon.)
• When it comes to solving Chemistry problems, our Calculator Pad is an awesome location for perfecting your skills. Try any one of the following sets of problems to level up you dilution problem-solving skills: Dilution Problems 1  ||  Dilution Problems 2
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.

 
 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
For Questions #1-3:
A sample of a stock solution of CuCl₂ is retrieved and diluted such that the final volume is 10 times greater than the sample’s original volume. Answer questions #1-3 based on this information.

1. The number of moles of CuCl₂ in the original sample is ______ the number of moles of CuCl₂ in the final sample.

1. the same as
2. 10 times greater than
3. 10 times less than
4. None of these

 


 
2. The molarity of CuCl₂ in the original sample is ______ the molarity of CuCl₂ in the final sample.

1. the same as
2. 10 times greater than
3. 10 times less than
4. None of these

 


 
3. When diluting a sample, a 10-fold increase in the volume of solution results in _____.

1. a 10-fold decrease in the number of moles of solute
2. a 10-fold increase in the number of moles of solute
3. a 10-fold decrease in the molarity of solute in the solution
4. a 10-fold increase in the molarity of solute in the solution
5. … Come on now! You can’t be certain about any of these things. It’s chemistry.

 
 

 
 
For Questions #4-5:
Three different diluted solutions - A, B, and C - are made by removing samples of varying volume from the same stock bottle and diluting it to a different final volume. The diagram below shows how Solutions A, B, and C are made. Answer questions #4-5 based on this information.
   
4. Rank the three solutions in order of the increasing number of moles of solute.
 



 
5. Rank the three solutions in order of the increasing molarity.

 


 
6. Mrs. Mandochino dissolves 5.52 grams of copper(II) nitrate – Cu(NO₃)₂ - in 500.0 mL of aqueous solution.

1. What is the molarity of the solution? 
   
   Check Answer
   Answer: 0.589 M
   
   This is a two-part problem. First, determine the moles of solute from the mass and the molar mass. Second, determine the molarity by dividing the moles of solute by the folume of solution - 0.5000 L.
   
   Cu(NO₃)₂ has a molar mass of 187.56 g/mol. The number of moles can be determined using molar mass as a conversion factor:
   
   5.52 g Cu(NO₃)₂ • (1 mol Cu(NO₃)₂ ) / (187.56 g Cu(NO₃)₂ ) = 0.02943058 ... mol Cu(NO₃)₂
   
   Now the molarity can be calculated from the moles and the volume (0.5000 L):
   
   [Cu(NO₃)₂] = (0.02943058 ... mol Cu(NO₃)₂) / (0.5000 L) = 0.58861 ... M = 0.589 M
   
    
   
    
2. She then draws 25.0 mL of the solution into a pipet. How many moles of copper(II) nitrate are in the pipet? 
   
   Check Answer
   Answer: 0.00147 mol Cu(NO₃)₂
   
   The molarity (unrounded) from Part a was 0.58861 ... M. The number of moles in 25.0 mL (0.0250 L) can be calculated as by using the molarity value - 0.58861 ... moles / 1 L - as a conversion factor:
   
   0.0250 L • (0.58861 ... mol) / (1 L solution) = 0.001471529 ... mol Cu(NO₃)₂ = 0.00147 mol Cu(NO₃)₂
   
    
   
    
3. Mrs. Mandochino empties the 25.0 mL into an empty volumetric flask and fills it to the 200.0 mL mark with distilled water. What is the molarity of this new solution? 
   
   Check Answer
   Answer: 0.00736 M
   
   The dilution equation can be used here:
   M_initial • V_initial = M_final • V_final
   
   We know: 
   M_initial = 0.058861164 ... M (unrounded, from Part b)
   V_initial = 0.0250 L
   V_final = 0.2000 L
   and we are looking to determing M_final.
   
   (0.058861164 ... M) • (0.0250 L) = M_final • (0.2000 L)
   
   Using a calculator, we get ...
   
   M_final = 0.007357646 ... M = 0.00736 M
   
   NOTE: an alternative means of determining the final molarity is to divide the number of moles from Part B by the final volume of 0.2000 L.
   
    
   
    

 
 
 
7. Mr. Glynch needs 800.0 mL of 1.500 M HCl solution for a lab. He will make the solution by diluting a concentrated solution (12.1 M) of HCl from a storeroom stock bottle. What volume (in mL) of 12.1 M HCl solution should he use?