Lesson 1: Atomic Mass and Atom Counting

Part a: Atomic Mass

Part a: Atomic Mass
Part b: Measuring Atomic Mass
Part c: The Mole
Part d: Grams-Moles-Atoms Relationship

 

The Amount of a Substance

As discussed in Chapter 1, Chemistry is a quantitative science. Numbers matter. Amounts are important. Chemists often need to know the amount of a substance in a particular sample. It’s a rather routine idea. A cook needs to know the amount of ingredients to combine to make an upcoming meal. And a chemist needs to know the amount of reactants to combine to make an intended product.
 
Amounts can be expressed in a number of ways. If you go to the hardware store to acquire some items for a home project, you might purchase a bag of items (a volume), two kilograms of items (a mass), or simply 10 items (a number). A cook may express amounts as a cup, a quart, a tablespoon, a teaspoon, and a pinch. A chemist can express amounts in terms of the mass of the sample, the volume of the sample, or the number of particles (atoms, molecules, or formula units) in the sample. In Lesson 1 of this chapter, we will learn how to determine the amount of a substance. Specific attention will be given to the amounts by mass and by atoms.
 
 
 

Atomic Mass

We first learned about isotopes in Chapter 3 of this Chemistry Tutorial. Elements consist of atoms. Every atom of an element has the same number of protons. This number is referred to as the atomic number. Atoms of an element may have a varying number of neutrons. The number of protons plus the number of neutrons is known as the mass number. Two atoms of the same element that have different numbers of neutrons are referred to as isotopes. The atomic number always identifies the type of atom – that is, the element. But the mass number will provide a measure of the mass of the atom.
 
Each cell of a Periodic Table lists the elemental symbol, the associated atomic number, the name of the element (sometimes), and the average atomic mass of the element. The average atomic mass is the number displayed below the symbol. Unlike the atomic number, the atomic mass is not a whole number. The average atomic mass value indicates the mass of an average atom of that element. We use the word average because an atom of any element has several isotopes. For example, carbon can have six neutrons (¹²C), seven neutrons (¹³C), or eight neutrons (¹⁴C). A sample of carbon will contain approximately 98.9% carbon-12, 1.1% carbon-13, and a very small amount of carbon-14. The average atomic mass value of carbon is 12.01. This is the weighted average based on the percent abundance of each isotope. You cannot find a carbon atom with a mass of 12.01. But the average atom (meaning an atom with a mass that is the weighted average of all the atoms) has a mass of 12.01.
 
 

 

 

The Carbon-12 Standard

You may have noticed something missing in the previous paragraph. Units!! There are no units mentioned for 12.01. The reason there are no units is the values mentioned for average atomic mass are relative values. They are values that are relative to all the other atomic mass values. We chemists are no fans of naked numbers. We think numbers should wear clothing and the units are the clothing. So we call the unit an atomic mass unit, abbreviated amu. Carbon has an average atomic mass of 12.01 amu. Now we no longer have to blush.
 

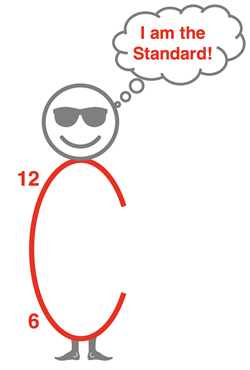
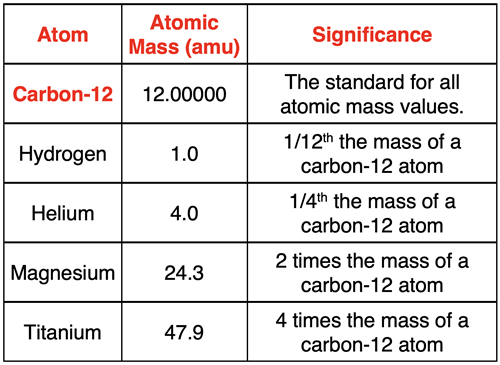
When expressing a collection of relative values, there must be some value that serves as the designated standard. All other values are expressed relative to that designated standard. The standard for the periodic table is the mass of the carbon-12 isotope. Carbon-12 with six protons and six neutrons is assigned the value of 12.000000 amu (exactly). All other atomic mass values are relative to the mass of carbon-12.
 
The average atomic mass of helium is 4.0 amu. So, the mass of an average helium atom is 1/3^rd the mass of a carbon-12 atom. The average atomic mass of hydrogen is 1.0 amu. So, the mass of an average hydrogen atom is 1/12^th the mass of a carbon-12 atom. The average atomic mass of a magnesium atom is 24.3 amu. So, the mass of an average magnesium atom is two times the mass of a carbon-12 atom. The average mass of a titanium atom is 47.9 amu, just short of 48 amu. So, the mass of an average titanium atom is about four times the mass of a carbon-12 atom. By designating a standard, we can compare the mass of atoms of various elements to one another … even though we cannot measure the mass of a single atom.
 

 
 

 
 

It’s All Relative

Because the carbon-12 isotope is the standard for all atomic mass values, the mass of all elements can be compared to carbon-12. But the comparisons don’t stop there. It logically follows that the mass of an atom of any element can be compared to the mass of an atom of any other element. For example, consider the following four elements:

 
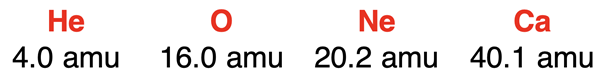
Based on the atomic mass values, the following assertions can be made:

• The mass of an O atom is ~4X the mass of a He atom.
• The mass of a Ne atom is ~5X the mass of a He atom.
• The mass of a Ca atom is ~10X the mass of a He atom.
• The mass of a Ca atom is ~2X the mass of a Ne atom.

 
These comparisons are just a few examples of the countless comparisons that can be made regarding the mass of one atom relative to another atom.
 
 
 

Comparing the Mass of a Collection of Atoms

The logic of comparing the mass of single atoms of different elements can be extended to comparisons of the mass of a collection of atoms. For example, let’s consider carbon with an average atomic mass of 12.01 amu and helium with an average atomic mass of 4.00 amu. The mass of an average carbon atom is three times the mass of an average helium atom. So, the mass of 1000 carbon atoms is approximately three times the mass of 1000 helium atoms. The mass of a million carbon atoms is approximately three times the mass of a million helium atoms. The mass of 6x10²³ carbon atoms is approximately three times the mass of a 6x10²³ helium atoms.
 
Let’s consider the following four elements again:
 

 

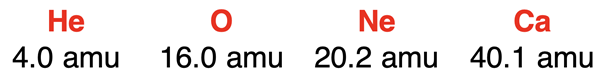
The following assertions can be made based on these atomic mass values:

• The mass of 1000 O atoms is approximately four times the mass of 1000 He atoms.
• The mass of 1000 Ne atoms is approximately five times the mass of 1000 He atoms.
• The mass of 1000 Ca atoms is approximately 10 times the mass of 1000 He atoms.
• The mass of 1000 Ca atoms is approximately two times the mass of 1000 Ne atoms.
• The mass of 6.0x10²³ O atoms is approximately four times the mass of 6.0x10²³ He atoms.
• The mass of 6.0x10²³ Ne atoms is approximately five times the mass of 6.0x10²³ He atoms.

 
 
The logic also works for comparing the mass of a different number of atoms of two different elements. Let’s consider carbon and helium once more. The mass of 1000 carbon atoms is approximately equal to the mass of 3000 helium atoms. The mass of a 10 million carbon atoms is approximately equal to the mass of 30 million helium atoms. The mass of 2x10²³ carbon atoms is approximately equal to the mass of a 6x10²³ helium atoms.
 
Let’s consider the following four elements again:
 

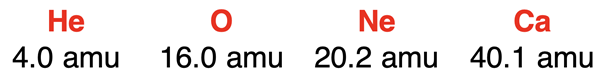
The following assertions can be made based on these atomic mass values:

• The mass of 1000 O atoms is approximately equal to the mass of 4000 He atoms.
• The mass of 1000 Ne atoms is approximately equal to the mass of 5000 He atoms.
• The mass of 1000 Ca atoms is approximately equal to the mass of 10 000 He atoms.
• The mass of 1000 Ca atoms is approximately equal to the mass of 2000 Ne atoms.
• The mass of 1.5x10²³ O atoms is approximately equal to the mass of 6.0x10²³ He atoms.
• The mass of 1.2x10²³ Ne atoms is approximately equal to the mass of 6.0x10²³ He atoms.

 
 
 

What About the Number of Atoms?

If you’re thinking (always recommended), then you might be saying under your breath (also recommended) something like …
   
That’s a great point. And you’re right!!! But we’re only on the first page of the Lesson. So, hang with us. Next, we will discuss how this mass information is determined. Then we will address your question – how can we use atomic mass to count the actual number of atoms?
 
 
 

Before You Leave

• Download our Study Card on Atomic Mass. Save it to a safe location and use it as a review tool. 
• Our Calculator Pad section has a set of Practice Problems on the topic. Your answers are evaluated and feedback is provided; you have infinite opportunites to correct your mistakes. Try Problem Set PMG2.
• The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.

 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. The atomic mass unit (amu) is particularly useful for expressing the mass of ______.

1. a single atom
2. samples of chemicals measured in labs
3. quantities of chemicals used in factories
4. ... nonsense! It's utterly useless.

 


 
2. Knowing the average atomic mass of carbon, scientists can count the number of atoms in a sample of any carbon with a known mass. Determine the number of carbon atoms in a sample of carbon having a mass of ...

1. ... 12.01 amu: ________________ atoms 
   
   Check Answer
   Answer: 1
   
   The atomic mass (mass of an average atom) of carbon is 12.01 amu.
   
    
   
    
2. ... 24.02 amu: ________________ atoms 
   
   Check Answer
   Answer: 2
   
   The atomic mass (mass of an average atom) of carbon is 12.01 amu. 24.01 amu is twice as much mass so it corresponds to twice the number of atoms.
   
    
   
    
3. ... 120.1 amu: ________________ atoms 
   
   Check Answer
   Answer: 10
   
   The atomic mass (mass of an average atom) of carbon is 12.01 amu. 120.1 amu is ten times as much mass so it corresponds to ten times the number of atoms.
   
    
   
    
4. ...865 amu: ________________ atoms 
   
   Check Answer
   Answer: 72
   
   The atomic mass (mass of an average atom) of carbon is 12.01 amu. 865 amu is 72 times as much mass so it corresponds to 72 times the number of atoms.
   
    
   
    

 
 
3. Compared to the mass of a helium atom, the mass of a …

1. … beryllium (Be) atom is ________ times greater. 
   
   Check Answer
   Answer: 2.25
   
   Use their average atomic masses and take the ratio:  9.01 / 4.00.
   
    
   
    
2. … nitrogen (N) atom is ________ times greater. 
   
   Check Answer
   Answer: 3.5
   
   Use their average atomic masses and take the ratio:  14.00 / 4.00.
   
    
   
    
3. … silicon (Si) atom is ________ times greater. 
   
   Check Answer
   Answer: ~7.02
   
   Use their average atomic masses and take the ratio:  28.08 / 4.00.
   
    
   
    
4. … sulfur (S) atom is ________ times greater. 
   
   Check Answer
   Answer: ~8.02
   
   Use their average atomic masses and take the ratio:  32.07 / 4.00.
   
    
   
    

 
 
4. For the following A/B comparisons, identify which has the greater mass and how many times greater the mass is.

1. A: 1 atom of nitrogen  vs.  B: 1 atom of silicon 
   
   Check Answer
   Answer: B; ~2 times greater
   
   Divide their atomic mass values: 28.08 /14.01
   
    
   
    
2. A: 1000 atoms of nitrogen  vs.  B: 1000 atoms of silicon 
   
   Check Answer
   Answer: B; ~2 times greater
   
   Since there is the same number of atoms of each element, divide their atomic mass values: 28.08 /14.01.
   
    
   
    
3. A: 1000 atoms of nitrogen  vs.  B: 2000 atoms of silicon 
   
   Check Answer
   Answer: B; ~4 times greater
   
   For equal number of atoms, there would be two times the mass for the silicon since the atomic mass ratio is : 28.08 /14.01. Since there are twice as many silicon atoms, you must multiply this ratio by 2.
   
    
   
    
4. A: 1000 atoms of nitrogen  vs.  B: 10 000 atoms of silicon 
   
   Check Answer
   Answer: B; ~20 times greater
   
   For equal number of atoms, there would be two times the mass for the silicon since the atomic mass ratio is : 28.08 /14.01. Since there are ten times as many silicon atoms, you must multiply this ratio by 10.
   
    
   
    
5. A: 2000 atoms of nitrogen  vs.  B: 1000 atoms of silicon 
   
   Check Answer
   Answer: The same
   
   For equal number of atoms, there would be two times the mass for the silicon since the atomic mass ratio is : 28.08 /14.01. Since there are two times as many nitrogen atoms, this offsets the fact that nitrogen has one-half the mass.
   
    
   
    
6. A: 10 000 atoms of nitrogen  vs.  B: 1000 atoms of silicon 
   
   Check Answer
   Answer: A, 5 times greater
   
   Nitrogen is one-half the mass of silicon. But with 10 times as many nitrogen atoms, multiply the one-half ratio by 10.
   
    
   
    

 
 
5. Consider the average atomic mass of neon (20.2 amu), argon (39.9 amu), and bromine (79.9 amu).

1. Approximately how many atoms of argon would have the same mass as 20 atoms of neon? 
   
   Check Answer
   Answer: ~10
   
   Argon has twice the mass as neon. So you only need one-half as many atoms to match the mass of the 20 atoms of neon.
   
    
   
    
2. Approximately how many atoms of bromine would have the same mass as 20 atoms of neon? 
   
   Check Answer
   Answer: ~5
   
   Bromine has four the mass as neon. So you only need one-fourth as many atoms to match the mass of the 20 atoms of neon.
   
    
   
    
3. Approximately how many atoms of bromine would have the same mass as 10 atoms of argon? 
   
   Check Answer
   Answer: ~5
   
   Bromine has twice the mass as argon. So you only need one-half as many atoms to match the mass of the 10 atoms of argon.
   
    
   
    
4. Approximately how many atoms of bromine would have the same mass as 100 atoms of argon? 
   
   Check Answer
   Answer: ~50
   
   Bromine has twice the mass as argon. So you only need one-half as many atoms to match the mass of the 100 atoms of argon.