Lesson 1: Physics in the Early 20th Century

Part b: The Photon

Part 1a: Emission Spectrum of the Elements
Part 1b: The Photon
Part 1c: Bohr's Quantized Energy Levels
Part 1d: Wave-Particle Duality
 

Blackbody Radiation

One of the puzzles confronting physicists at the end of the 19^th century was a phenomenon known as blackbody radiation. A blackbody is an object that absorbs all the electromagnetic energy that strikes it, thus increasing its temperature. The increase in temperature causes particles to vibrate or oscillate. These vibrating particles release energy as electromagnetic radiation of varying wavelengths (and frequencies). In a less-than-ideal way, most objects behave in a way that resembles a blackbody - absorbing energy, warming up, and radiating electromagnetic radiation to the surroundings. A classic example of an ordinary object radiating energy would be the red-hot glow of a wood log in a fireplace.
 
A blackbody radiates energy across a broad range of wavelengths. The peak wavelength is related to the glow color of the object. The peak wavelength and color changes as the temperature of the blackbody increases. Most objects at ordinary temperatures emit radiation in the infrared region and do not have a visible glow. As temperatures increase past 500°C, a visible glow begins to appear. Physicists were very aware of the data. The trouble spot was that the data did not agree with their theories regarding the electromagnetic radiation being released by the blackbody.
 
In 1900, German physicist Max Planck approached the problem quite differently than the classical approach. Planck proposed that the radiation emitted by blackbodies was quantized. Instead of releasing a continuous range of energies, blackbodies released only certain discrete energy values. The energy (E) is directly proportional to the frequency (f) and inversely proportional to the wavelength (λ), following the equations

 
In Planck’s equations, h is a constant known as Planck’s constant. It has a value of 6.626x10^-34 J•s. The unit J represents the standard metric unit of energy, the joule. The symbol c is the speed of light, known to be 3.00x10⁸ m/s. Finally, n in the equations is known as a quantum number and has integer values of 1, 2, 3, … . The inclusion of the quantum number in the equation means that the energy emitted by a blackbody is restricted to being some whole number multiple of h•f or of h•c/λ. It is the quantum number that quantizes the energy radiated by blackbodies so that there are only certain allowed values.
 

 
 

 

Quantized Light Energy

After hearing of Planck’s concept of quantized energy, Albert Einstein proposed that light has a particle nature to it. After all, it the energy released by matter is quantized, then the light itself must exist as quanta of light. Einstein imagined a beam of light as being a stream of particles. He referred to the particles as photons and indicated that a photon was simply a bundle of energy, h•f. A bright beam was concentrated with many photons, each having an energy of h•f. And a dim beam had much fewer photons, but each having an energy of h•f. The variables were thus the frequency, f, and the number of photons, n, present in a beam. A violet beam would have a have photons with a greater frequency than the photons of a red beam. The energy of every photon would be h•f where the frequency is associated with the color of the light.

 
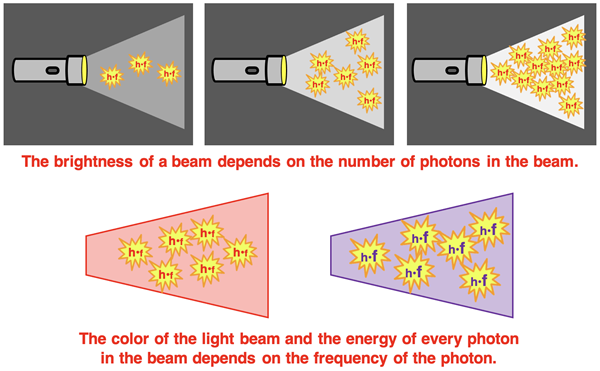
Einstein’s particle view was in stark contrast to the classical wave view of light. Waves spread across space, do not have mass or volume, and are described by a wavelength and a frequency. Particles were perceived as being exclusive to waves. Particles are not described by a wavelength or a frequency, but as having a mass and a volume, and as occupying a distinct location in space. So, what was Einstein up to in suggesting that light consisted of particles, bundles of energy in the amount h•f? We will approach this question later in Lesson 1. But for now, let’s examine how Einstein used the idea to solve another problem troubling physicists – the photoelectric effect.
 

 
 

 

The Photoelectric Effect

If you shine light upon a metal surface, an electron may be ejected from the metal surface. This is known as the photoelectric effect. The effect can be studied with an apparatus similar to that shown at the right. Electrons are ejected with a range of kinetic energies. Those ejected from surface atoms have the maximum kinetic energy. The kinetic energy of the ejected electrons can be measured by adjusting the voltage.
 
 
The classical thought on the photoelectric effect had two basic flaws:

1. Flaw #1: It was believed that any frequency of light would be capable of ejecting an electron as long as it was intense enough. This was not found to be the case. There was a minimum frequency that was required in order to eject the electron. Increasing intensity had no effect upon whether an electron was ejected or not.
2. Flaw #2: It was believed that increasing the intensity of the light would increase the maximum kinetic energy of the electron. This was not found to the case. Increasing the intensity only caused more electrons to be ejected; intensity had no effect upon the kinetic energy of the ejected electron.

 
Einstein used the idea of a photon to explain the unexpected results. Ejecting an electron from a metal requires a minimum amount of energy. The amount of energy possessed by a photon depends on its frequency and is given by h•f. Photons of higher frequency possess more energy. So, a photon of violet light has more energy than a photon of red light. A red light’s photon energy may not be enough to eject an electron from a given material. Increasing the intensity of the red light beam does not increase the energy of the red photon. It simply concentrates more red photons in the beam, each of which has insufficient energy to eject an electron from the metal. A less intense violet beam may be quite capable of ejecting the electrons since violet photons have sufficient energy. Increasing the intensity of the violet beam causes more electrons to be ejected. But since intensity does not affect the energy of the photon, it doesn’t cause the kinetic energy of the electron to be changed.
   
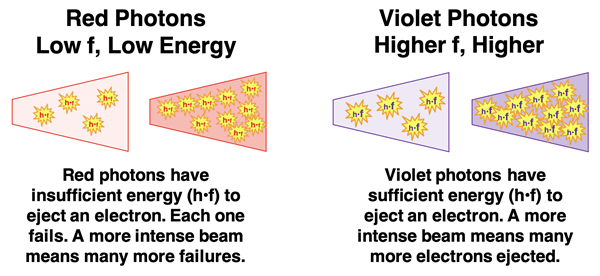
Einstein’s analysis comes down to photons and energy conservation. Suppose it takes 500 units of energy to eject an electron from a surface atom of the metal. If the incoming photon has 300 units of energy (red photon), then an electron will not be ejected. Having more photons with this energy won’t produce any better results. But suppose the incoming photon has 600 units of energy (violet photon). An electron will be ejected from the surface atom (using up 500 units of energy), and it will have a kinetic energy of 100 units. Increasing the intensity of the violet beam (i.e., the number of photons with 600 units of energy) will cause more electrons to be ejected from the surface atoms. But each electron still has 100 units of kinetic energy.
       

Energy Changes in Atoms

Max Planck birthed the quantum model. Albert Einstein promoted it. Einstein modeled most behaviors using the concept of light consisting of photons and photons being bundles of energy. It made perfect sense to Einstein that if a photon strikes an atom with 200 units of energy, then there must be a change of 200 units of energy within the atom. An electron could transition from energy level to another energy level that is 200 units higher. Or if the material is a metal and 150 units is all that is required to eject an electron, Einstein expects an electron to be ejected with 50 units of kinetic energy.
 
Similarly, if an electron in an excited energy state transitions to an energy state that is 300 units lower in energy, then Einstein believes a photon will be released with 300 units of energy. If an electron in an excited energy state transitions to a ground state that is 500 units lower in energy, then Einstein believes a photon will be released with 500 units of energy. And the photon with 500 units of energy will have a different frequency than the photon with 300 units of energy. For Einstein this is simple accounting. The currency is energy. The photon is the carrier of that energy.
 
Now all that is needed is for a scientist to implement the idea of energy quanta in order to explain the structure of the atom and the emission spectra of the elements. That’s the topic of the next page of Lesson 1.
 
 
 
 
 

Before You Leave

• Try our simulation on The Photoelectric Effect. Change a variable and observe an effect or non-effect.
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.

 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. In what way does increasing temperature affect the peak wavelength of blackbody radiation?

1. Increasing temperature increases the peak wavelength.
2. Increasing temperature decreases the peak wavelength.
3. Increasing temperature has no effect on the peak wavelength.

 


 
2. In what way does increasing temperature affect the peak frequency of blackbody radiation?

1. Increasing temperature increases the peak frequency.
2. Increasing temperature decreases the peak frequency.
3. Increasing temperature has no effect on the peak frequency.

   ​


 
3. Astronomers spot two stars in a distant galaxy – one is glowing red and the other has a blue glow to it. What can be concluded about the temperatures of these stars?

1. The red star has a higher temperature.
2. The blue star has a higher temperature.
3. We could never be sure about the temperature of anything that far away.

  ​


 
4. According to Einstein, a photon can best be described as a ______.

1. light wave with a wavelength and a frequency
2. light wave with a frequency but no wavelength
3. light particle that contains a discrete quantity of energy

  ​


 
5. Suppose electromagnetic radiation is directed towards a sheet of metal but there are no electrons ejected. Which one of the following changes would likely produce the hoped-for result of electrons being emitted?

1. Increase the intensity of the radiation.
2. Decrease the intensity of the radiation.
3. Increase the frequency of the radiation.
4. Decrease the frequency of the radiation.

 

​


 
6. It is known that electrons will be ejected from a metal surface if photons having 250 units of energy are shone on the surface. What will be the maximum kinetic energy of an ejected electron if 300 units are shone of the surface?
 
  ​