The Physics Classroom » The Review Session » 1-D Kinematics » Answers

One-Dimensional Kinematics Review

Navigate to:

Review Session Home - Topic Listing

1D Kinematics - Home || Printable Version || Questions and Links

Answers to Questions: #1-7 || #8-#28 || #29-#42 || #43-#50
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 ]

Part A: Multiple TRUE/FALSE

1. Which of the following statements about vectors and scalars are TRUE? List all that apply.

A vector is a large quantity and a scalar is a small quantity.
A scalar quantity has a magnitude and a vector quantity does not.
A vector quantity is described with a direction and a scalar is not.
Scalar quantities are path dependent quantities and vector quantities are not.
A scalar quantity depends only upon the initial and final values of the quantity; this is not the case for vector quantities.
The quantity 20 m/s, north is a speed and as such is a scalar quantity.
The quantity 9.8 m/s/s is an acceleration value and as such is a vector quantity.

Answer: CD

a. FALSE - This would never be the case. Vectors simply are direction-conscious, path-independent quantities which depend solely upon the initial and final state of an object. Vectors are always expressed fully by use of a magnitude and a direction.

b. FALSE - Both scalar and vector quantities have a magnitude or value expressed with a given unit; additionally, a vector quantity requires a direction in order to fully express the quantity.

c. TRUE - Vectors are fully described by magnitude AND direction; scalars are not described with a direction.

d. TRUE - Scalars such as distance would depend upon the path taken from initial to final location. If you run around the track one complete time, your distance will be different than if you take a step forward and a step backwards. The path MATTERS; distance (like all scalars) depends upon it. On the other hand, the displacement (a vector quantity) is the same for both paths.

e. FALSE - Vectors are the types of quantities which depend only upon initial and final state of the object. For instance, the vector quantity displacement depends only upon the starting and final location.

f. FALSE - This is certainly not a speed quantity; though the unit is appropriate for speed, the statement of the direction is inconsistent with speed as a scalar quantity.

g. FALSE (a rather picky FALSE) - If a direction was included, then this would be an acceleration value. The unit is characteristic of acceleration but the lack of direction is inconsistent with acceleration being a vector quantity.

Useful Web Link

Vectors and Scalars

[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 ]

2. Which of the following statements about distance and/or displacement are TRUE? List all that apply.

Distance is a vector quantity and displacement is a scalar quantity.
A person makes a round-trip journey, finishing where she started. The displacement for the trip is 0 and the distance is some nonzero value.
A person starts at position A and finishes at position B. The distance for the trip is the length of the segment measured from A to B.
If a person walks in a straight line and never changes direction, then the distance and the displacement will have exactly the same magnitude.
The phrase "20 mi, northwest" likely describes the distance for a motion.
The phrase "20 m, west" likely describes the displacement for a motion.
The diagram below depicts the path of a person walking to and fro from position A to B to C to D. The distance for this motion is 100 yds.
For the same diagram below, the displacement is 50 yds.

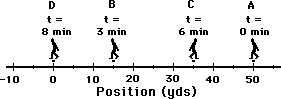
Answer: BDF

a. FALSE - Distance is the scalar and displacement is the vector. Know this one!

b. TRUE - Displacement is the change in position of an object. An object which finishes where it started is not displaced; it is at the same place as it started and as such has a zero displacement. On the other hand, the distance is the amount of ground which is covered. And if it was truly a journey, then there is definitely a distance.

c. FALSE - This would only be the case if the person walk along a beeline path from A to B. But if the person makes a turn and veers left, then right and then ..., then the person has a distance which is greater than the length of the path from A to B. Distance refers to the amount of ground which is covered.

d. TRUE - If a person never changes direction and maintains the same heading away from the initial position, then every step contributes to a change in position in the same original direction. A 1 m step will increase the displacement (read as out of place-ness) by 1 meter and contribute one more meter to the total distance which is walked.

e. FALSE - Distance is a scalar and is ignorant of direction. The "northwest" on this quantity would lead one to believe that this is a displacement (a vector quantity) rather than a distance.

f. TRUE - The unit is an appropriate displacement unit (length units) and the direction is stated. Since there is both magnitude and direction expressed, one would believe that this is likely a displacement.

g. FALSE - The distance from A to B is 35 yds; from B to C is 20 yds; and from C to D is 35 yds. The total distance moved is 90 yds.

h. FALSE (a rather picky FALSE) - Technically, this is not a displacement since displacement is a vector and fully described by both magnitude and direction. The real expression of displacement is 50 yds, left (or west or -)

Useful Web Link

Distance vs. Displacement

3. Which of the following statements about velocity and/or speed are TRUE? List all that apply.

Velocity is a vector quantity and speed is a scalar quantity.
Both speed and velocity refer to how fast an object is moving.
Person X moves from location A to location B in 5 seconds. Person Y moves between the same two locations in 10 seconds. Person Y is moving with twice the speed as person X.
The velocity of an object refers to the rate at which the object's position changes.
For any given motion, it is possible that an object could move very fast yet have an abnormally small velocity.
The phrase "30 mi/hr, west" likely refers to a scalar quantity.
The average velocity of an object on a round-trip journey would be 0.
The direction of the velocity vector is dependent upon two factors: the direction the object is moving and whether the object is speeding up or slowing down.
The diagram below depicts the path of a person walking to and fro from position A to B to C to D. The entire motion takes 8 minutes. The average speed for this motion is approximately 11.3 yds/min.
For the same diagram below, the average velocity for this motion is 0 yds/min.

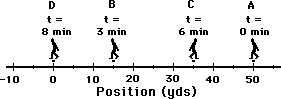
Answer: ADEGI

a. TRUE - Yes! Speed is a scalar and velocity is the vector. Know this one!

b. FALSE - Speed refers to how fast an object is moving; but velocity refers to the rate at which one's motion puts an object away from its original position. A person can move very fast (and thus have a large speed); but if every other step leads in opposite directions, then that person would not have a large velocity.

c. FALSE - Person Y has one-half the speed of Person X. If person Y requires twice the time to do the same distance, then person Y is moving half as fast.

d. TRUE - Yes! That is exactly the definition of velocity - the rate at which position changes.

e. TRUE - An Indy Race car driver is a good example of this. Such a driver is obviously moving very fast but by the end of the race the average velocity is essentially 0 m/s.

f. FALSE - The presence of the direction "west" in this expression rules it out as a speed expression. Speed is a scalar quantity and direction is not a part of it.

g. TRUE - For a round trip journey, there is no ultimate change in position. As such, the average velocity is 0 m/t seconds. Regardless of the time, the average velocity will be 0 m/s.

h. FALSE - The direction of the velocity vector depends only upon the direction that the object is moving. A westward moving object has a westward velocity.

i. TRUE - As discussed in #2g, the distance traveled is 90 meters. When divided by time (8 minutes), the average speed is 11.25 yds/min.

j. FALSE - The average velocity would be 0 yds/min only if the person returns to the initial starting position. In this case, the average velocity is 50 yds/8 min, west (6.25 yds/min, west).

Useful Web Link

Speed vs. Velocity

4. Which of the following statements about acceleration are TRUE? List all that apply.

Acceleration is a vector quantity.
Accelerating objects MUST be changing their speed.
Accelerating objects MUST be changing their velocity.
Acceleration units include the following; m/s², mi/hr/sec, cm/s², km/hr/m.
The direction of the acceleration vector is dependent upon two factors: the direction the object is moving and whether the object is speeding up or slowing down.
An object which is slowing down has an acceleration.
An object which is moving at constant speed in a circle has an acceleration.
Acceleration is the rate at which the velocity changes.
An object that is accelerating is moving fast.
An object that is accelerating will eventually (if given enough time) be moving fast.
An object that is moving rightward has a rightward acceleration.
An object that is moving rightward and speeding up has a rightward acceleration.
An object that is moving upwards and slowing down has an upwards acceleration.

Answer: ACEFGHL (and maybe J)

a. TRUE - Yes it is. Acceleration is direction-conscious.

b. FALSE - Accelerating objects could be changing their speed; but it is also possible that an accelerating object is only changing its direction while maintaining a constant speed. The race car drivers at Indy might fit into this category (at least for certain periods of the race).

c. TRUE - Accelerating object MUST be changing their velocity -either the magnitude or the direction of the velocity.

d. FALSE - The first three sets of units are acceleration units - they include a velocity unit divided by a time unit. The last set of units is a velocity unit divided by a length unit. This is definitely NOT an acceleration.

e. TRUE - This is the case and something important to remember. Consider its application in the last three parts of this question.

f. TRUE - Accelerating objects are either slowing down, speeding up or changing directions.

g. TRUE - To move in a circle is to change one's direction. As such, there is a change in the velocity (not magnitude, but the direction part); this constitutes an acceleration.

h. TRUE - This is the very definition of acceleration. Know this one - its the beginning point of all our thoughts about acceleration.

i. FALSE - Accelerating objects are not necessarily moving fast; they are merely changing how fast they are moving (or the direction they are moving).

j. FALSE - If the accelerating object is slowing down, then it will eventually stop and not reach a fast speed. And if that doesn't convince you, then consider an object that is accelerating by moving in a circle at constant speed forever; it will accelerate the entire time but never being going any faster than at the beginning.

k. FALSE - If an object is moving rightward and slowing down, then it would have a leftward acceleration.

l. TRUE - If an object is speeding up, then the direction of the acceleration vector is in the direction which the object is moving.

m. FALSE - If an object is slowing down, then the acceleration vector is directed opposite the direction of the motion; in this case the acceleration is directed downwards.

Useful Web Link

Acceleration

5. Which of the following statements about position-time graphs are TRUE? List all that apply.

Position-time graphs cannot be used to represent the motion of objects with accelerated motion.
The slope on a position-time graph is representative of the acceleration of the object.
A straight, diagonal line on a position-time graph is representative of an object with a constant velocity.
If an object is at rest, then the position-time graph will be a horizontal line located on the time-axis.
Accelerated objects are represented on position-time graphs by curved lines.
An object with a positive velocity will be represented on a position-time graph by a line with a positive slope.
An object with a negative velocity will be represented on a position-time graph by a line with a negative slope.
An object with a positive acceleration will be represented on a position-time graph by a line which curves upwards.
An object with a negative acceleration will be represented on a position-time graph by a line which curves downwards.

Answer: CEFG

a. FALSE - Position-time graphs represent accelerated motion by curved lines.

b. FALSE - The slope of a position-time graph is the velocity of the object. Some things in this unit are critical things to remember and internalize; this is one of them.

c. TRUE - A straight diagonal line is a line of constant slope. And if the slope is constant, then so is the velocity.

d. FALSE - Not necessarily true. If the object is at rest, then the line on a p-t graph will indeed be horizontal. However, it will not necessarily be located upon the time axis.

e. TRUE - Accelerating objects (if the acceleration is attributable to a speed change) are represented by lines with changing slope - i.e., curved lines.

f. TRUE - Since slope on a p-t graph represents the velocity, a positive slope will represent a positive velocity.

g. TRUE - Since slope on a p-t graph represents the velocity, a negative slope will represent a negative velocity.

h. FALSE - (This is confusing wording here since we might not all agree on what "curving up" means.) A line that slopes upward and has a curve (perhaps you call that "curving up" as I do) has a positive velocity (due to its positive slope). If the curve is "concave down" (you might say leveling off to a horizontal as time progresses) then the object is slowing down and the acceleration is negative.

i. FALSE - (Once more, there is confusing wording here since we might not all agree on what "curving downwards" means.) A line that slopes downwards and has a curve (perhaps you call that "curving downwards " as I do) has a negative velocity (due to its negative slope). If the curve is "concave up" (you might say leveling off to a horizontal as time progresses) then the object is slowing down and the acceleration is positive.

Useful Web Link

The Meaning of Shape for a p-t Graph | The Meaning of Slope for a p-t Graph

6. Which of the following statements about velocity-time graphs are TRUE? List all that apply.

The slope on a velocity-time graph is representative of the acceleration of the object.
The area on a velocity -time graph is representative of the change in position of the object.
An accelerated object's motion will be represented by a curved line on a velocity-time graph.
Objects with positive acceleration will be represented by upwardly-curved lines on a velocity-time graph.
If an object is at rest, then the velocity-time graph will be a line with zero slope.
A line with zero slope on a velocity-time graph will be representative of an object which is at rest.
A line with a negative slope on a velocity-time graph is representative of an object with negative velocity.
If an object changes its direction, then the line on the velocity-time graph will have a changing slope.
An object which is slowing down is represented by a line on a velocity-time graph which is moving in the downward direction.

Answer: ABE (and almost D)

a. TRUE - Now this is important! It is the beginning point of much of our discussion of velocity-time graphs. The slope equals the acceleration.

b. TRUE - This is equally important. The area is the displacement.

c. FALSE - An object which has an acceleration will be represented by an line that has a slope. It may or may not curve, but it must have a slope other than zero.

d. FALSE - An object with positive acceleration will have an positive or upward slope on a v-t graph. It does not have to be a curved line. A curved line indicates an object that is accelerating at a changing rate of acceleration.

e. TRUE - An object that is at rest has a 0 velocity and maintains that zero velocity. The permanence of its velocity (not the fact that it is zero) gives the object a zero acceleration. and as such, the line on a v-t graph would have a slope of 0 (i.e., be horizontal).

f. FALSE - A line with zero slope is representative of an object with an acceleration of 0. It could be at rest or it could be moving at a constant velocity.

g. FALSE - A negative slope indicates a negative acceleration. The object could be moving in the positive direction and slowing down (a negative acceleration).

h. FALSE - An object which changes its direction will be represented by a line on a v-t graph that crosses over the time-axis from the + velocity region into the - velocity region.

i. FALSE - An object which is slowing down has a velocity which is approaching 0 m/s. And as such, on a v-t graph, the line must be approaching the v=0 m/s axis.

Useful Web Link

The Meaning of Shape for a v-t Graph | The Meaning of Slope for a v-t Graph | Relating the Shape to the Motion

7. Which of the following statements about free fall and the acceleration of gravity are TRUE? List all that apply.

An object that is free-falling is acted upon by the force of gravity alone.
A falling skydiver which has reached terminal velocity is considered to be in a state of free fall.
A ball is thrown upwards and is rising towards its peak. As it rises upwards, it is NOT considered to be in a state of free fall.
An object in free fall experiences an acceleration which is independent of the mass of the object.
A ball is thrown upwards, rises to its peak and eventually falls back to the original height. As the ball rises, its acceleration is upwards; as it falls, its acceleration is downwards.
A ball is thrown upwards, rises to its peak and eventually falls back to the original height. The speed at which it is launched equals the speed at which it lands. (Assume negligible air resistance.)
A very massive object will free fall at the same rate of acceleration as a less massive object.
The value of g on Earth is approximately 9.8 m/s².
The symbol g stands for the force of gravity.

Answer: ADFGH

a. TRUE - Yes! This is the definition of free fall.

b. FALSE - Skydivers which are falling at terminal velocity are acted upon by large amounts of air resistance. They are experiencing more forces than the force of gravity. As such, they are NOT free-falling.

c. FALSE - Any object - whether rising, falling or moving horizontally and vertically simultaneously - can be in a state of free fall if the only force acting upon it is the force of gravity. Such objects are known as projectiles and often begin their motion while rising upwards.

d. TRUE - The unique feature of free-falling objects is that the mass of the object does not effect the trajectory characteristics. The acceleration, velocity, displacement, etc. is independent of the mass of the object.

e. FALSE - The acceleration of all free-falling objects is directed downwards. A rising object slows down due to the downward gravity force. An upward-moving object which is slowing down is said to have a downwards acceleration.

f. TRUE - If the object is truly in free-fall, then the speed of the object will be the same at all heights - whether its on the upward portion of its trajectory or the downwards portion of its trajectory. For more information, see the Projectiles page at The Physics Classroom.

g. TRUE - The acceleration of free-falling objects (referred to as the acceleration of gravity) is independent of mass. On Earth, the value is 9.8 m/s/s (the direction is down). All objects - very massive and less massive - experience this acceleration value.

h. TRUE - Yes! Know this one!

i. FALSE - Nope. A careful physics teacher will never call g the force of gravity. g is known as the acceleration of gravity. It might be best to call it the acceleration caused by gravity. When it comes to the force of gravity, we have yet another symbol for that - F_grav. But that's a topic to be discussed in a later unit.

Useful Web Link

Introduction to Free Fall | The Acceleration of Gravity

Part B: Multiple Choice

8. If an object has an acceleration of 0 m/s², then one can be sure that the object is not ____.

a. moving

b. changing position

c. changing velocity

Answer: C

The object could be moving and could be at rest; however, whether moving or not, it must not have a changing velocity.

Useful Web Link

Acceleration

9. If car A passes car B, then car A must be ____.

accelerating.
accelerating at a greater rate than car B.
moving faster than car B and accelerating more than car B.
moving faster than car B, but not necessarily accelerating.

Answer: D

All that is necessary is that car A has a greater speed (is moving faster). If so, it will eventually catch up and pass car B. Acceleration is not necessary to overcome car B; a car going 60 mi/hr at a constant speed will eventually pass a car going 50 mi/hr at a constant speed. Surely you have witnessed that while driving down a local highway.

Useful Web Link

Acceleration | Speed vs. Velocity

10. Which one of the following is NOT consistent with a car which is accelerating?

A car is moving with an increasing speed.
A car is moving with a decreasing speed.
A car is moving with a high speed.
A car is changing direction.

Answer:

An accelerating object must be changing its velocity by either slowing down, speeding up or changing direction. Moving fast merely means that the velocity is high; it says nothing about the acceleration.

Useful Web Link

Acceleration

11. A fullback is running down the football field in a straight line. He starts at the 0-yard line at 0 seconds. At 1 second, he is on the 10-yard line; at 2 seconds, he is on the 20-yard line; at 3 seconds, he is on the 30-yard line; and at 4 seconds, he is on the 40-yard line. This is evidence that

he is accelerating
he is covering a greater distance in each consecutive second.
he is moving with a constant speed (on average).

Answer: C

The fullback is moving 10 yards every second. He has a constant speed and thus covers the same distance (10 yd) in each consecutive second. He is not accelerating.

Useful Web Link

Acceleration | Speed vs. Velocity

12. A fullback is running down the football field in a straight line. He starts at the 0-yard line at 0 seconds. At 1 second, he is on the 10-yard line; at 2 seconds, he is on the 20-yard line; at 3 seconds, he is on the 30-yard line; and at 4 seconds, he is on the 40-yard line. What is the player's acceleration?

Answer: 0 m/s/s

The fullback is moving 10 yards every second. He has a constant speed. He also is running in a straight line, so he is not changing direction. Thus, his acceleration is 0 m/s/s. Only objects with changing velocity have a nonzero acceleration.

Useful Web Link

Acceleration | Speed vs. Velocity

13. Olympic gold medalist Michael Johnson runs one time around the track - 400 meters - in 38 seconds. What is his displacement? ___________ What is his average velocity? ___________

Answer: d = 0 m and v = 0 m/s

Michael finishes where he started, so he is not "out of place." His displacement is 0 meters. Since average velocity is displacement over time, his average velocity is also 0 m/s.

Useful Web Link

Distance vs. Displacement | Speed vs. Velocity

14. If an object is moving eastward and slowing down, then the direction of its velocity vector is ____.

a. eastward

b. westward

c. neither

d. not enough info to tell

Answer: A

The direction of the velocity vector is always in the same direction as the direction which the object moves.

Useful Web Link

Speed vs. Velocity

15. If an object is moving eastward and slowing down, then the direction of its acceleration vector is ____.

a. eastward

b. westward

c. neither

d. not enough info to tell

Answer: B

If an object is slowing down, then the direction of the acceleration vector is in the opposite direction as the direction which the object moves. (If the object were speeding up, the acceleration would be eastward.)

Useful Web Link

Acceleration

16. Which one of the following quantities is NOT a vector?

a. 10 mi/hr, east

b. 10 mi/hr/sec, west

c. 35 m/s, north

d. 20 m/s

Answer: D

A vector has both magnitude and direction. Only choice d does not show a direction; it must be a scalar.

Useful Web Link

Scalars vs. Vectors

17. Which one of the following quantities is NOT a speed?

a. 10 mi/hr

b. 10 mi/hr/sec

c. 35 m/s

d. 20 m/s

Answer: B

You can often tell a quantity by its units. 10 mi/hr/sec is an acceleration since there are two time units involved. In fact, the units are velocity change units (mi/hr) per time units (seconds). The quantity speed has units of distance/time.

Useful Web Link

Speed vs. Velocity

18. Which one of the following statements is NOT true of a free-falling object? An object in a state of free fall ____.

falls with a constant speed of -10 m/s.
falls with a acceleration of -10 m/s/s.
falls under the sole influence of gravity.
falls with downward acceleration which has a constant magnitude.

Answer: A

A free-falling object is an object upon which the only force is gravity. As it falls, it accelerates at a rate of approx. 10 m/s/s. This acceleration value is constant during the entire trajectory of the motion. Since this is the case, the speed can not be constant.

Useful Web Link

Introduction to Free Fall | The Acceleration of Gravity

19. The average speed of an object which moves 10 kilometers (km) in 30 minutes is ____.

a. 10 km/hr

b. 20 km/hr

c. 30 km/hr

d. more than 30 km/hr

Answer: B

The average speed is distance/time. In this case the distance is 10 km and the time is 0.5 hr (30 minutes). Thus

average speed = (10 km)/(0.5 hr) = 20 km/hr

Useful Web Link

Speed vs. Velocity

20. What is the acceleration of a car that maintains a constant velocity of 55 mi/hr for 10.0 seconds?

a. 0

b. 5.5 mi /hr/s

c. 5.5 mi /s/s

d. 550 mi/hr/s

Answer: A

If the velocity is constant, then there is no acceleration. That is, the value of the acceleration is 0.

Useful Web Link

Acceleration

21. As an object freely falls, its ____.

a. speed increases	b. acceleration increases
c. both of these	d. none of these

Answer: A

As an object falls, it accelerates; this means that the speed will be changing. While falling, the speed increases by 10 m/s every second. The acceleration is a constant value of 10 m/s/s; thus, choice b should not be chosen.

Useful Web Link

Introduction to Free Fall | The Acceleration of Gravity

22. A speedometer is placed upon a free-falling object in order to measure its instantaneous speed during the course of its fall. Its speed reading (neglecting air resistance) would increase each second by ____.

a. about 5 m/s	b. about 10 m/s	c. about 15 m/s
d. a variable amount	e. depends on its initial speed.

Answer: B

The acceleration of gravity is approximately 10 m/s/s. Acceleration represents the rate at which the velocity changes - in this case, the velocity changes by 10 m/s every second. So the speed will increase by the amount of 10 m/s every second.

Useful Web Link

The Acceleration of Gravity | Kinematic Equations and Free Fall

23. Ten seconds after being dropped from rest, a free-falling object will be moving with a speed of ____.

a. about 10 m/s.

b. about 50 m/s.

c. about 100 m/s.

d. more than 100 m/s.

Answer: C

Since the speed of a free-falling object increases by 10 m/s every second, the speed after ten of these seconds will be 100 m/s. You could use the kinematic equation

v_f = v_i + a*t

where v_i=0 m/s and a = -10 m/s/s and t=10 s

Useful Web Link

The Acceleration of Gravity | Kinematic Equations and Free Fall

24. A baseball pitcher delivers a fast ball. During the throw, the speed of the ball increases from 0 to 30.0 m/s over a time of 0.100 seconds. The average acceleration of the baseball is ____ m/s².

a. 3.00

b. 30.0

c. 300.

d. 3000

e. none of these

Answer: C

Acceleration is velocity change over time. In this problem, the velocity change is +30.0 m/s and the time is 0.100 s. Thus,

a = (+30.0 m/s)/(0.100 s) = 300. m/s/s.

Useful Web Link

Acceleration

25. On takeoff, a rocket accelerates from rest at a rate of 50.0 m/s² for exactly 1 minute. The rocket's speed after this minute of steady acceleration will be ____ m/s.

a. 50.0

b. 500.

c. 3.00 x 10³

d. 3.60 x 10³

e. none of these

Answer: C

Use the equation

v_f= v_i + a*t

v_f = 0 + (50.0 m/s/s)*(60.0 s) = 3.00 x 10³ m/s

(Note that the unit on time must be the same as the time units for which the acceleration is given.)

Useful Web Link

Acceleration

26. When a rock is dropped, it will accelerate downward at a rate of 9.8 m/s². If the same rock is thrown downward (instead of being dropped from rest), it acceleration will be ____. (Ignore air resistance effects.)

a. less than 9.8 m/s²

b. 9.8 m/s²

c. more than 9.8 m/s²

Answer: B

Whether rising or falling, if the sole force acting upon the object is gravity, then the acceleration is 9.8 m/s/s (often approximated as 10 m/s/s).

Useful Web Link

Introduction to Free Fall | The Acceleration of Gravity

27. Consider drops of water that leak from a dripping faucet at a constant rate. As the drops fall they ____.

a. get closer together	b. get farther apart
c. remain at a relatively fixed distance from one another

Answer: B

Since the drops of water are falling (and probably free-falling), they should be getting farther apart as they fall. This is because the free-falling drops are accelerating and thus gaining speed.

Useful Web Link

Introduction to Free Fall | The Acceleration of Gravity

28. Renatta Oyle is again found driving her '86 Yugo down Lake Avenue, leaving the following trail of oil drops on the pavement.

If her car is moving from right to left, then ...

her velocity has a rightward direction and her acceleration has a rightward direction.
her velocity has a rightward direction and her acceleration has a leftward direction.
her velocity has a leftward direction and her acceleration has a rightward direction.
her velocity has a leftward direction and her acceleration has a leftward direction.

Answer: D

The car is heading leftward and the velocity is always in the same direction as the direction which the object moves. Since the car is speeding up, the acceleration is leftward. Whenever an object speeds up, its acceleration is in the same direction which the object moves. Whenever an object slows down, its acceleration is in the opposite direction which the object moves.

Useful Web Link

Ticker Tape Diagrams | The Acceleration

Part C: Diagramming

29. On the diagrams below, construct a dot diagram representing the motion of an object with a ... .

constant rightward velocity
rightward velocity and a rightward acceleration
rightward velocity and a leftward acceleration
rightward velocity, first slow and constant, and then accelerating to a high speed
rightward velocity, first decelerating from a high speed to a rest position, then maintaining the rest position, and finally accelerating at a lower rate than the initial deceleration.

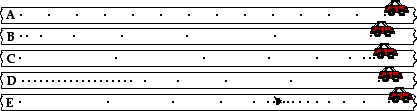
Answer: See diagram above; explanations are given below.

a. A constant velocity is depicted by dots which are spaced the same distance apart.

b. An object which is accelerating in the same direction as the velocity (both are rightward in this case) is speeding up. And so as you trace your eye from left to right across the diagram (rightward), the dots should be spaced further and further apart to indicate that the object is speeding up.

c. An object that moves rightward (i.e., rightward velocity) and accelerating leftwards must be slowing down. And so as you trace your eye from left to right across the diagram (rightward), the dots should be spaced closer and closer together to indicate that the object is slowing down.

d. The dots begin by being equally spaced (constant speed) and close together (slow); then the spacing between dots become gradually further and further apart to indicated the speeding up nature of the motion.

e. The object is moving rightwards so you will need to trace your eye from left to right across the diagram (rightward). As you do you will note that the dots become closer and closer to indicate that the object is slowing down. Then the dots are piled onto the same location to indicate that the object is at rest. Finally, the dots are spread further and further apart; the rate at which the distance between dots is very gradual - consistent with the statement that the rate of acceleration is less than the original rate of deceleration.

30. On a dot diagram, how does the motion of an object moving to the right and slowing down differ from an object moving to the left and speeding up? Explain.

Answer: There is no difference!

The two diagrams would be indistinguishable from each other as indicated by the following two diagrams.

There are two ways to accelerate leftward; and regardless of how it happens, the oil drop trace would be identical. A leftward acceleration is a leftward acceleration.

Useful Web Link

Ticker Tape Diagrams

Part D: Kinematic Graphing

31. On the position-time graph below, sketch a plot representing the motion of an object which is ... . Label each line with the corresponding letter (e.g., "a", "b", "c", etc.)

at rest.
moving in the positive direction with constant speed
moving in the negative direction and speeding up
moving in the positive direction and slowing down
moving in the positive direction at a constant speed (slow) and then later fast at constant speed
moving with a negative velocity and a negative acceleration
moving with a negative velocity and a positive acceleration

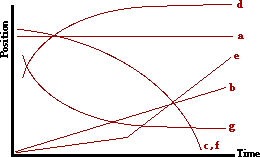
Answer: See diagram above; explanations are given below.

The governing principle in this problem is that the slope of a position-time graph is equal to the velocity of the object.

a. An object at rest (v = 0 m/s) is represented by a line with 0 slope (horizontal line).

b. An object with a constant, positive velocity is represented by a straight line (constant slope) which slopes upward (positive slope).

c. An object moving in the - direction and speeding up is represented by a line which slopes downward (- slope) and increases its steepness (increasing slope).

d. An object moving in the + direction and slowing down is represented by a line which slopes upward (+ slope) and increases its steepness (increasing slope).

e. An object moving in the positive direction at constant speed would be represented by a straight diagonal line (constant speed) which slopes upward (+ velocity). So in this case, there will be two straight diagonal lines; the second line will slope more than the first line.

f. An object moving in the negative direction with negative acceleration is speeding up (since the a vector is in the same direction as the motion). So on a p-t graph, this object will be represented by a line which slopes downwards (- velocity) and increases its slope over time (speeding up).

g. An object moving in the negative direction with positive acceleration is slowing down (since the a vector is in the opposite direction as the motion). So on a p-t graph, this object will be represented by a line which slopes downwards (- velocity) and levels off or becomes more horizontal over time (slowing down).

Useful Web Link

The Meaning of Shape for a p-t Graph | The Meaning of Slope for a p-t Graph | The Meaning of Shape for a v-t Graph |Relating the Shape to the Motion

32. On the velocity-time graph below, sketch a plot representing the motion of an object which is ... . Label each line with the corresponding letter (e.g., "a", "b", "c", etc.)

at rest
moving in the positive direction at constant speed
moving in the negative direction from slow to fast
moving in the negative direction from fast to slow
moving with a positive velocity and a positive acceleration
moving with a positive velocity and a negative acceleration
moving with a positive velocity at constant speed and then decelerating to a rest position
moving in the positive direction while slowing down, changing directions and moving in the negative directions while speeding up

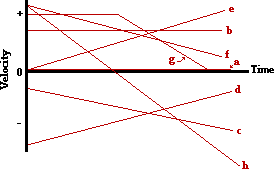
Answer: See diagram above; explanations are given below.

The governing principle in this problem is that the slope of a velocity-time graph is equal to the acceleration of the object. Furthermore, a negative velocity would be a line plotted in the negative region of the graph; a positive velocity would be a line plotted in the positive region of the graph.

a. An object at rest (v = 0 m/s) is represented by a line located on the time axis (where v = 0 m/s).

b. An object moving in the positive direction at constant speed will be represented on a v-t graph by a horizontal line (slope = a = 0 m/s/s) positioned in the + velocity region.

c. An object moving in the negative direction and speeding up will be represented on a v-t graph by a sloped line located in the - velocity region. Since such an object has a - acceleration, the line will slope downwards (- acceleration).

d. An object moving in the negative direction and slowing down will be represented on a v-t graph by a sloped line located in the - velocity region. Such an object has a positive acceleration (since it is slowing down, the a vector will be in the opposite direction of the motion). The + acceleration would be consistent with a line that slopes upwards.

e. An object moving with a + velocity and a + acceleration would be represented on a v-t graph by a sloped line located in the + velocity region. The + acceleration would be consistent with a line that slopes upwards.

f. An object moving with a + velocity and a - acceleration would be represented on a v-t graph by a sloped line located in the + velocity region. The - acceleration would be consistent with a line that slopes downwards.

g. An object moving with a constant + velocity would be represented on a v-t graph by a horizontal line (slope = a = 0 m/s/s) located in the + velocity region. The slowing down to rest portion of the graph would be represented by a line which slopes downwards (- acceleration) towards the time axis.

Useful Web Link

The Meaning of Shape for a p-t Graph | The Meaning of Slope for a p-t Graph | The Meaning of Shape for a v-t Graph |Relating the Shape to the Motion

33. Consider the position-time plots below. Sketch the shape of the corresponding velocity-time graphs.

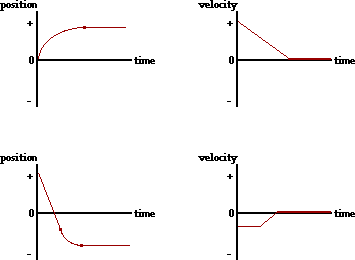
Answer: See diagram above; explanations are given below.

In the top graph, the object moves in the + direction with an acceleration from fast to slow until it finally stops. Then the object remains at rest. This means there is a positive velocity and a negative acceleration; the final velocity of the object is 0 m/s. So on a v-t graph, the line needs to be in the +velocity region and the slope needs to be - (for a negative acceleration). The line should end on the v=0 m/s axis (corresponding to its final rest position).

In the bottom graph, the object is moving in the - direction with a constant speed. It then gradually slows down until it stops; it then remains at rest. So on a v-t graph, there should be a horizontal line (a=0 m/s/s) in the -velocity region of the graph. Then the line should slope upwards (for the + acceleration that is characteristic of objects moving in the - direction and slowing down). The line should end on the v=0 m/s axis (corresponding to its final rest position).

Useful Web Link

The Meaning of Shape for a p-t Graph | The Meaning of Slope for a p-t Graph | The Meaning of Shape for a v-t Graph |Relating the Shape to the Motion

34. Consider the velocity-time plots below. Sketch the shape of the corresponding position-time graphs.

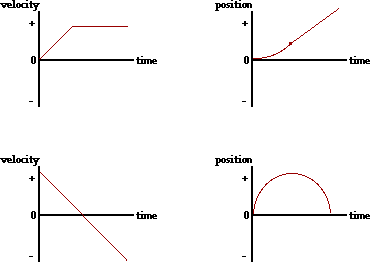
Answer: See diagram above; explanations are given below.

In the top graph, the object moves in the + direction with an acceleration from slow to fast. Then the object maintains a constant speed by walking in the same direction (+ direction). On a p-t graph, this would correspond to a line with positive slope (for moving in the + direction) which eventually straightens out into a diagonal line with constant slope (constant speed) in the positive direction (positive velocity).

In the bottom graph, the object is moving in the + direction and slowing down from a high speed to a slow speed until it finally changes direction; the object then moves in the - direction and speeds up. On a p-t graph, this would correspond to a line with positive slope (for moving in the + direction) which gradually levels off to a horizontal (for slowing down); then the line begins to slope downwards (for moving in the - direction) and gradually becomes steeper and steeper (for speeding up).

Useful Web Link

The Meaning of Shape for a p-t Graph | The Meaning of Slope for a p-t Graph | The Meaning of Shape for a v-t Graph |Relating the Shape to the Motion

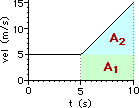
The velocity-time graph below depicts the motion of an automobile as it moves through Glenview during rush hour traffic. Use the graph to answer questions #35 - #39.

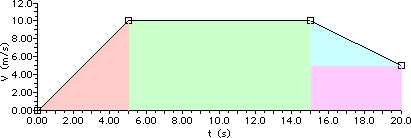
35. Determine the displacement of the automobile during the following intervals of time. PSYW

Answer: See diagram above and calculations below.

Use area calculations to determine the displacement of the object.

t = 0 s - 5 s	t = 5 s - 15 s	t = 15 s - 20 s
Area of the pink triangle: A = 0.5bh A = 0.5(5 s)(10 m/s) A = 25 m	Area of the green rectangle: A = bh A = (10 s)(10 m/s) A = 100 m	Area of the blue triangle plus purple rectangle: A = 0.5b₁h₁ + b₂h₂ A = 0.5(5 s)(5 m/s) + (5 s)(5 m/s) A = 12.5 m + 25 m A = 37.5 m

Useful Web Link

Determining the Area on a v-t Graph

36. Determine the velocity of the automobile at the following instant(s) in time.

Answer: See calculations below.

It is a velocity graph; so merely read the velocity values off the graph.

t = 3 s

t = 8 s

t = 17 s

v = 6.0 m/s

v = 10.0 m/s

v = 8.0 m/s

37. Determine the acceleration of the automobile during the following intervals of time.

Answer: See calculations below.

Do slope calculations to determine the acceleration. Slope is rise/run.

t = 0 s - 5 s	t = 5 s - 15 s	t = 15 s - 20 s
a = slope = rise/run a = (10 m/s)/(5 s) a = 2.0 m/s/s	a = slope = rise/run a = (0 m/s)/(10 s) a = 0.0 m/s/s	a = slope = rise/run a = (-5 m/s)/(5 s) a = -1.0 m/s/s

Useful Web Link

The Meaning of Slope for a v-t Graph | Determining the Slope on a v-t Graph

38. Using complete sentences and the language of physics, describe the motion of the automobile during the entire 20.0 seconds. Explicitly describe any changes in speed or direction which might occur; identify intervals of time for which the automobile is at rest, the automobile is moving with constant speed, or the automobile is accelerating.

Answer:

During the first 5 seconds, the auto is moving with a + velocity and a + acceleration, increasing its speed from slow to fast. From 5 s to 15 s, the auto is moving with a constant speed and a zero acceleration. From 15 s to 20 s, the auto is moving with a +velocity and a - acceleration, decreasing its speed from fast to slow.

Useful Web Link

The Meaning of Shape for a v-t Graph | Relating the Shape to the Motion

39. Supposing the automobile has an oil leak, demonstrate your understanding of its motion by drawing an oil drop diagram for the 20.0 seconds of motion. Divide the diagram into three distinct time intervals (0.0 - 5.0 seconds, 5.0 - 15.0 seconds, 15.0 - 20.0 seconds).

Answer: See Diagram and explanation below.

In the first five seconds, the object is speeding up so the spacing between dots will gradually increase. In the next ten seconds (5-15 s) the object is maintaining a constant velocity so the spacing between dots remains the same. In the last 5 seconds (15-20 s) the object is slowing down so the spacing between dots is gradually decreasing.

Useful Web Link

The Meaning of Slope for a v-t Graph | Determining the Slope on a v-t Graph | Ticker Tape Diagrams

40. For the plots below, determine the velocity of the object ... .

a. from 0.0 - 5.0 seconds	b. from 5.0 - 10.0 seconds	c. at 13.0 seconds

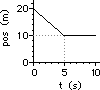
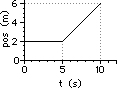
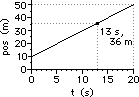
Answer: See explanations and calculations below.

For a position-time graph, the velocity is determined from a slope calculation. So in each case, two points must be picked and slope calculation must be performed.

a. Pick the two points: (0 s, 20 m) and (5 s, 10 m)

slope = rise/run = (-10 m)/(5 s) = -2.0 m/s

b. Pick the two points: (5 s, 2 m) and (10 s, 6 m)

slope = rise/run = (4 m)/(5 s) = +0.80 m/s

c. From 0 to 20 s, the slope is a constant value. So determining the slope at 13 seconds is as simple as merely determining the slope of the line choosing any two points. So just pick the two points: (0 s, 10 m) and (20 s, 50 m)

slope = rise/run = (40 m)/(20 s) = +2.0 m/s

Useful Web Link

The Meaning of Slope for a p-t Graph | Determining the Slope for a p-t Graph

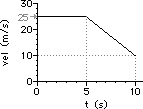
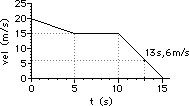
41. For the plots below, determine the acceleration of the object ... .

a. from 0.0 - 5.0 seconds	b. from 5.0 - 10.0 seconds	c. at 13.0 seconds

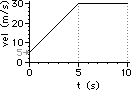
Answer: See explanations and calculations below.

For a velocity-time graph, the acceleration is determined from a slope calculation. So in each case, two points must be picked and slope calculation must be performed.

a. Pick the two points: (0.0 s, 5.0 m/s) and (5.0 s, 30.0 m/s)

slope = rise/run = (25.0 m/s)/(5.0 s) = +5.0 m/s²

b. Pick the two points: (5.0 s, 25.0 m/s) and (10.0 s, 10.0 m/s)

slope = rise/run = (-15 m/s)/(5.0 s) = -3.0 m/s²

c. From 10.0 to 15.0 s, the slope is a constant value. So determining the slope at 13 seconds is as simple as merely determining the slope of the line choosing any two points. So just pick the two points: (10.0 s, 15.0 m/s) and (15.0 s, 0.0 m/s)

slope = rise/run = (-15.0 m/s)/(5.0 s) = -3.0 m/s

Useful Web Link

The Meaning of Slope for a v-t Graph | Determining the Slope on a v-t Graph

42. For the plots below, determine the displacement of the object ... .

a. from 0.0 - 5.0 seconds	b. from 5.0 - 10.0 seconds	c. from 0.0 - 15.0 seconds

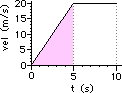
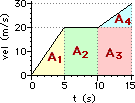
Answer: See explanations and calculations below.

For velocity-time graphs, the displacement of an object is found by computing the area between the line and the time axis. The shape is typically a rectangle (area = base*height), a triangle (area = 0.5*base*height) or a trapezoid (which can typically be transformed into a rectangle and a triangle or the area can be computed as 0.5*(h₁ + h₂)*base).

a. Area = 0.5*base*height = 0.50*(5.0 s)*(20.0 m/s) = 50. m

b. Area = A₁ + A₂ (see diagram) = (5.0 s)*(5.0 m/s) + 0.50*(5.0 s)*(10.0 m/s) = 25 m + 25 m = 50. m

c. Area = A₁ + A₂ + A₃ + A₄ (see diagram)

Area = 0.5*(5.0 s)*(20.0 m/s) + (5.0 s)*(20.0 m/s) + (5.0 s)*(20.0 m/s) + 0.5*(5.0 s)*(10.0 m/s)

Area = 50 m + 100 m + 100 m + 25 m = 275 m

Useful Web Link

The Meaning of Slope for a v-t Graph | Determining the Slope on a v-t Graph

Part E: Computational Problems

43. Determine the acceleration (in m/s²) of an object which ... .

moves in a straight line with a constant speed of 20.0 m/s for 12.0 seconds
changes its velocity from 12.1 m/s to 23.5 m/s in 7.81 seconds
changes its velocity from 0.0 mi/hr to 60.0 mi/hr in 4.20 seconds
accelerates from 33.4 m/s to 18.9 m/s over a distance of 109 m

Answer: See answers, explanations and calculations below.

a. If the speed and direction of an object is constant, then the acceleration is 0 m/s².

b. The acceleration is the velocity change per time ratio:

a = (Velocity Change)/t = (23.5 m/s - 12.1 m/s) / (7.81 s) = 1.46 m/s².

c. The acceleration is the velocity change per time ratio:

a = (Velocity Change)/t = (60.0 mi/hr - 0.0 mi/hr) / (4.20 s) = 14.3 mi/hr/s.

14.3 mi/hr/s * (1.0 m/s) / (2.24 mi/hr) = 6.38 m/s².

d. The acceleration value can also be calculated using kinematic equations if three other kinematic quantities are known. In this case, the know information is: v_o = 33.4 m/s; v_f = 18.9 m/s; and d = 109 m. Using the equation v_f² = v_o² + 2*a*d, the acceleration can be computed.

a = (v_f² - v_o²) / (2*d) = [(18.9 m/s)² - (33.4 m/s)² ] / (2 * 109 m) = -3.48 m/s².

Useful Web Link

Acceleration | The Kinematic Equations | Kinematic Equations and Problem-Solving | Sample Problems and Solutions

44. Determine the magnitude of the displacement (in meters) of an object which ... .

moves from Hither to Yon (with an average speed of 28.0 m/s) and then back to Hither (with an average speed of 28.0 m/s) if both the forward and the return trip take 46 minutes each.
moves at a constant speed of 8.30 m/s in a straight line for 15.0 seconds.
decelerates at a rate of -4.35 m/s/s from a speed of 38.1 m/s to a speed of 17.6 m/s
accelerates from rest at a rate of 3.67 m/s² for 12.1 seconds
is moving at 12.2 m/s and then accelerates at a rate of +1.88 m/s² for 17.0 seconds

Answer: See answers, explanations and calculations below.

a. Since this is a round-trip journey, the overall displacement is 0 m.

b. Since the velocity is constant, the displacement can be found by multiplying the velocity by the time.

d = v*t = (8.30 m/s) * (15.0 s) = 125 m

c. A displacement value can also be calculated using kinematic equations if three other kinematic quantities are known. In this case, the know information is: v_o = 38.1 m/s; v_f = 17.6 m/s; and a = -4.35 m/s/s. Using the equation v_f² = v_o² + 2*a*d, the displacement can be computed.

d = (v_f² - v_o²) / (2*a) = [(17.6 m/s)² - (38.1 m/s)² ] / (2 * -4.35 m/s/s) = 131 m.

d. A displacement value can be calculated using other kinematic equations if a different set of kinematic quantities is known. Here we know that: v_o = 0.0 m/s; t = 12.1 s; and a = 3.67 m/s/s. Using the equation d = v_o* t + 0.5*a*t², the displacement can be computed.

d = ~~(0 m/s)*(12.1 s)~~ + 0.5*(3.67 m/s/s)*(12.1 s)²= 269 m.

e. Here the displacement value is calculated using the same kinematic equation. We know that: v_o = 12.2 m/s; t = 17.0 s; and a = 1.88 m/s/s. Using the equation d = v_o* t + 0.5*a*t², the displacement can be computed.

d = (12.2 m/s)*(17.0 s) + 0.5*(1.88 m/s/s)*(17.0 s)²= 479 m.

Useful Web Link

Distance and Displacement | The Kinematic Equations | Kinematic Equations and Problem-Solving | Sample Problems and Solutions

45. The hare is sleeping at a location that is 1200 m from the finish line. The tortoise passes him at a steady speed of 5.0 cm/s. If the hare finally wakes up 6.5 hours later, then what minimum acceleration (assumed constant) must he have in order to pass the tortoise before the finish line.

Answer: 0.0067 m/s²

Like a lot of physics word problems, there is more than one path to the final answer. In all such problems, the solution involves thought and good problem-solving strategies (draw a picture, list what you know, list pertinent equations, etc.).

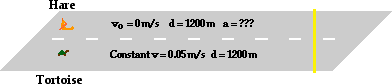
The tortoise, moving at a constant speed, will cover the 1200 m in a time of:

t_tortoise = d/v_tortoise = (1200 m) / (0.050 m/s) = 24000 s = 6.666... hrs

The hare will sleep for 6.5 hrs (23400 s) before starting, and so will have only 0.1666... hrs (600 s) to accelerate to the finish line. So the acceleration of the hare can be determine using a kinematic equation. The know information about the hare's motion is: t = 600 s; d = 1200 m; v_o = 0 m/s. The best equation is d = v_o* t + 0.5*a*t². The v_o* t term cancels and the equation can be algebraically rearranged and solved for a:

a = 2*d / t² = 2 * (1200 m) / (600 s)² = 0.0067 m/s².

Useful Web Link

The Kinematic Equations | Kinematic Equations and Problem-Solving | Sample Problems and Solutions

46. A Gold Car moving at 12.0 m/s passes a Green Car while the Green Car is at rest at a stoplight. The Green Car immediately accelerates at a rate of +1.80 m/s/s for 11.0 seconds seconds and then maintains a constant speed. After how much time (relative to the initial starting time) must the Green Car drive before catching up with the Gold Car.

Answer: 14.0 s

(As mentioned in the previous problem ...) Like a lot of physics word problems, there is more than one path to the final answer. In all such problems, the solution involves thought and good problem-solving strategies (draw a picture, list what you know, list pertinent equations, etc.).

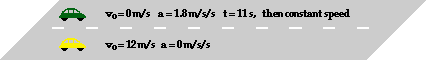
Here the gold car travels with a constant speed for a time of t seconds (where t is the total time of travel for both cars). The distance traveled by the gold car is given by the kinematic equation d = v_o* t + 0.5*a*t². The second term cancels and the distance can be expressed as

d = v_o* t ~~+ 0.5*a*t²~~ = (12.0 m/s)*t, or

d_gold = 12.0* t

For the green car, there is an accelerated period and then a constant speed period. The distance traveled during the accelerated period (d_1green) is found from the same kinematic equation. For the green car, the first term cancels and the distance is

d_1green = ~~v_o* t +~~ 0.5*a*t² = 0.5*(1.80 m/s²)*(11.0 s)², or

d_1green = 108.9 m

Once the green car has accelerated for 11 seconds, it maintains a constant speed for the remaining time, given by the expression t - 11 s. The speed at which the green car is traveling during this time can be computed using the equation:

v_fgreen = v_o + a*t = (1.80 m/s²) *(11.0 s) = 19.8 m/s

The distance traveled by the green car during this constant speed portion of its motion (d_2green) can be computed using the kinematic equation. d = v_o* t + 0.5*a*t². The second term cancels and the distance can be expressed as

d_2green = v_o* t ~~+ 0.5*a*t²~~ = (19.8 m/s) * (t - 11 s) = 19.8*t - 217.8, or

d_2green= 19.8*t - 217.8

So the total distance traveled by the green car is given by the expression:

d_green = d_1green + d_2green = 108.9 + 19.8*t - 217.8

d_green = 19.8*t - 108.9

When the green car catches up to the gold car their distance traveled will be the same. So the time t can be determined by setting the two expressions for distance equal to each other and solving for t.

12.0* t = 19.8*t - 108.9

108.9 = 7.80*t

t = (108.9) / (7.80)

t = 13.96 s = 14.0 s

Useful Web Link

The Kinematic Equations | Kinematic Equations and Problem-Solving | Sample Problems and Solutions

47. Ima Rilla Saari is cruising at 28.0 m/s down Lake Avenue and through the forest preserve. She notices a deer jump into the road at a location 62.0 m in front of her. Ima first reacts to the event, then slams on her brakes and decelerates at -8.10 m/s², and ultimately stops a picometer in front of the frozen deer. What is Ima's reaction time? (i.e., how long did it take Ima to react to the event prior to decelerating?)

Answer: 0.486 s

Ima's total distance traveled (62.0 m) can be broken into two segments - a reaction distance (d_rxn) and a braking distance (d_braking). The reaction distance is the distance Ima moves prior to braking; she will move at constant speed during this time of t_rxn. The braking distance is the distance which Ima moves when her foot is on the brake and she decelerates from 28.0 m/s to 0.0 m/s. The braking distance can be computed first using the following kinematic equation: v_f² = v_o² + 2*a*d. The known information for this braking period is: v_o = 28 m/s; v_f = 0 m/s; and a = -8.10 m/s/s. The substitutions and solution are shown below.

d_braking = (v_f² - v_o²) / (2*a) = [(0 m/s)² - (28.0 m/s)² ] / (2 * -8.10 m/s/s) = 48.40 m.

Since Ima's car requires 48.40 m to brake, she can travel a maximum of 13.6 m during the reaction period. The relationship between reaction time, speed and reaction distance is given by the equation

d_rxn = v * t_rxn

Substituting 13.6 m for d_rxn and 28.0 m/s for v, the reaction time can be computed:

t_rxn = (13.6 m) / (28.0 m/s) = 0.486 s

Useful Web Link

The Kinematic Equations | Kinematic Equations and Problem-Solving | Sample Problems and Solutions

48. A two-stage rocket accelerates from rest at +3.57 m/s/s for 6.82 seconds. It then accelerates at +2.98 m/s/s for another 5.90 seconds. After the second stage, it enters into a state of free fall. Determine:

the maximum speed
the maximum altitude
the height of the rocket after 20.0 seconds
the total time the rocket is in the air (assuming it is launched from the ground)

Answer: See answers and explanations below.

This problem can be approached by either the use of a velocity-time graph or the use of kinematic equations (or a combination of each). Whatever the approach, it is imperative to break the multistage motion up into its three different acceleration periods. The use of kinematic equations is only appropriate for constant acceleration periods. For this reason, the complex motion must be broken up into time periods during which the acceleration is constant. These three time periods can be seen on the velocity-time graph by three lines of distinctly different slope. The diagram at the right provides a depiction of the motion; strategic points are labeled. These points will be referred to in the solutions below. The velocity-time plot below will be used throughout the solution; note that the same strategic points are labeled on the plot.

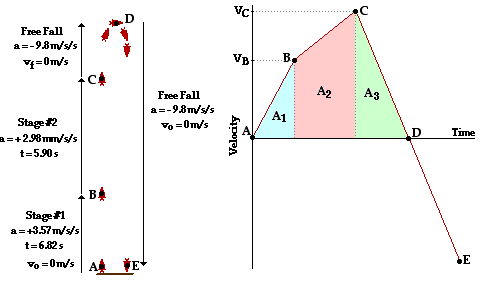
a. The maximum speed occurs after the second stage or acceleration period (point C). After this time, the upward-moving rocket begins to slow down as gravity becomes the sole force acting upon it. To determine this speed (v_c), the kinematic equation v_f = v_o + a*t will be used twice - once for each acceleration period.

First Stage: v_B = v_A + a*t = 0 m/s + (3.57 m/s/s) * (6.82 s) = 24.3 m/s

Second Stage: v_C = v_B + a*t = 24.3 m/s + (2.98 m/s/s) * (5.90 s) = 41.9 m/s

b. The maximum altitude occurs at point D, sometime after the second stage has ceased and the rocket finally runs out of steam. The velocity at this point is 0 m/s (it is at the peak of its trajectory). The altitude at this point is the cumulative distance traveled from t = 0 s to t = t_D. This distance is the distance for the first stage, the second stage and the deceleration period (C to D). These distances correspond to the area on the v-t graph; they are labeled A₁, A₂, and A₃ on the graph. They are calculated and summed below.

A₁= 0.5*b*h = 0.5 * (24.3 m/s) * (6.82 s) = 82.86 m

A₂= b*h + 0.5*b*h (a triangle on top of a square)

A₂= (24.3 m/s) * (5.9 s) + 0.5 * (41.9 m/s - 24.3 m/s) * (5.9 s) = 195.42 m

It will be necessary to know the time from point C to point D in order to determine A₃. This time can be determined using the kinematic equation v_f = v_o + a*t for which v_f = 0 m/s and v_o = 41.9 m/s and a = -9.8 m/s/s.

v_D = v_C + a*t

0 m/s = 41.9 m/s + (-9.8 m/s/s) * t

t = 4.28 s

Now A₃ can be determined using the v-t graph. The area is a triangle and is calculated as

A₃= 0.5*b*h = 0.5 * (41.9 m/s) * (4.82 s) = 89.57 m

The maximum altitude is the sum of the three distances (areas)

Max. altitude = 82.86 m + 195.42 m + 89.57 m = 368 m

c. When the rocket reaches point D, the time is 17.0 seconds. The altitude at 20.0 seconds will be the 368 meters risen above the launch pad from point A to point D minus the distance fallen from the peak from 17.0 to 20.0 seconds. This distance would be represented by a negative area on the velocity-time graph. The area is a triangle and can be computed if the velocity at 20 seconds is known. It can be calculated using a kinematic equation and then used to determine the area of a triangle. Alternatively, a kinematic equation can be used to determine the distance fallen during these 3.0 seconds. The work is shown below:

d = ~~v_o* t~~ + 0.5*a*t² = 0.5 * (-9.8 m/s/s) * (3.0 s)² = 44.1 m

The altitude at 20 seconds is therefore the ~369 m risen in the first 17 seconds minus the ~44 m fallen in the next 3 seconds. The answer is 325 m.

d. The rocket rises 369 m in the first 17.0 seconds. In the time subsequent of this, the rocket must fall 369 meters. The time to fall 369 m can be found from the same kinematic equation used in part c.

d = ~~v_o* t~~ + 0.5*a*t²

-368 m = 0.5 * (-9.8 m/s/s) * t²

t = 8.67 seconds

This time can be added onto the 17.0 seconds to determine the time at which the rocket lands: 25.7 seconds.

Useful Web Link

The Kinematic Equations | Kinematic Equations and Problem-Solving | Sample Problems and Solutions

49. In a 200.0-m relay race (each leg of the race is 50.0 m long), one swimmer has a 0.450 second lead and is swimming at a constant speed of 3.90 m/s towards the opposite end of the pool. What minimum speed must the second swimmer have in order to catch up with the first swimmer by the end of the pool?

Answer: 4.04 m/s

Both swimmers swim the same distance (50 m) at constant speed. Swimmer A (who was just arbitrarily named) gets a 0.450 second head start. So swimmer B must travel faster in order to finish the race in less time than swimmer A. First, the time required of swimmer A to complete the 50l0 m at 3.90 m/s can be computed. The time is

t_A = d/v_A = (50.0 m) / (3.90 m/s) = 12.82 s

Thus, swimmer B must finish the same 50.0 m in 12.37 seconds (12.82s - 0.45 s). So the speed of swimmer B can be computed as

v_B = d/t_B = (50.0 m) / (12.37 s) = 4.04 m/s

Useful Web Link

The Kinematic Equations | Kinematic Equations and Problem-Solving | Sample Problems and Solutions

50. A drag racer accelerates from rest at an average rate of +13.2 m/s² for a distance of 100. m. The driver coasts for 0.500 seconds and then uses the brakes and parachute to decelerate until the end of the track. If the total length of the track is 180. m, what minimum deceleration rate must the racer have in order to stop prior to the end of the track?

Answer: -24 m/s/s

This problem can be approached by first determining the distance over which the dragster decelerates. This distance will be less than 80. meters by an amount equal to the distance which the dragster coasts after crossing the finish line. See diagram.

The distance traveled by the dragster prior to braking is 100 m plus the coasting distance. The coasting distance can be determined if the speed of the dragster at the end of 100 m is determined. So first, a kinematic equation will be used to determine the speed and then the coasting distance will be computed.

Using the equation v_f² = v_o² + 2*a*d, the speed after 100 m can be determined. This substitution and solution is shown below.

v_f² = ~~v_o²~~ + 2*a*d = 2*(13.2 m/s/s)*(100. m) = 2640 m²/s²

v_f = 51.4 m/s

Coasting at 51.38 m/s for 0.500 s will lead to a distance traveled of 25.7 m.

Once the coasting period is over, there is a short distance left to decelerate to a stop. This distance is

180. m - 100. m - 25.7 m = 54 m

Now the same kinematic equation can be used to determine the deceleration rate during the last 54 m of the track. Known information is: v_o = 51.4 m/s; v_f = 0 m/s; and d = 54 m. Using the equation v_f² = v_o² + 2*a*d, the acceleration can be computed.

a = (v_f² - v_o²) / (2*d) = = [(51.4 m/s)² - (0 m/s)² ] / (2 * 54 m) = -24 m/s².

Useful Web Link

The Kinematic Equations | Kinematic Equations and Problem-Solving Sample Problems and Solutions

Navigate to:

Review Session Home - Topic Listing

1D Kinematics - Home || Printable Version || Questions and Links

Answers to Questions: #1-7 || #8-#28 || #29-#42 || #43-#50

You Might Also Like ...

Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:

The Calculator Pad

The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.

Visit: The Calculator Pad Home | Calculator Pad - Kinematics
Minds On Physics the App Series

Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 1 of the series includes Kinematic Concepts and Kinematic Graphing.

Visit: MOP the App Home || MOP the App - Part 1