Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 As mentioned earlier in Lesson 4, a standing wave pattern is an interference phenomenon. It is formed as the result of the perfectly timed interference of two waves passing through the same medium. A standing wave pattern is not actually a wave; rather it is the pattern resulting from the presence of two waves of the same frequency with different directions of travel within the same medium.
As mentioned earlier in Lesson 4, a standing wave pattern is an interference phenomenon. It is formed as the result of the perfectly timed interference of two waves passing through the same medium. A standing wave pattern is not actually a wave; rather it is the pattern resulting from the presence of two waves of the same frequency with different directions of travel within the same medium.
What are Nodes and Antinodes?
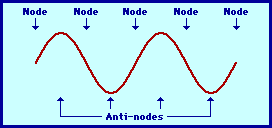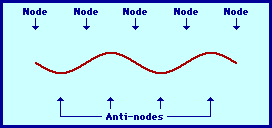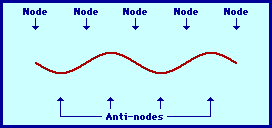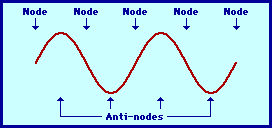
One characteristic of every standing wave pattern is that there are points along the medium that appear to be standing still. These points, sometimes described as points of no displacement, are referred to a s nodes. There are other points along the medium that undergo vibrations between a large positive and large negative displacement. These are the points that undergo the maximum displacement during each vibrational cycle of the standing wave. In a sense, these points are the opposite of nodes, and so they are called antinodes. A standing wave pattern always consists of an alternating pattern of nodes and antinodes. The animation shown below depicts a rope vibrating with a standing wave pattern. The nodes and antinodes are labeled on the diagram. When a standing wave pattern is established in a medium, the nodes and the antinodes are always located at the same position along the medium; they are standing still. It is this characteristic that has earned the pattern the name standing wave.
s nodes. There are other points along the medium that undergo vibrations between a large positive and large negative displacement. These are the points that undergo the maximum displacement during each vibrational cycle of the standing wave. In a sense, these points are the opposite of nodes, and so they are called antinodes. A standing wave pattern always consists of an alternating pattern of nodes and antinodes. The animation shown below depicts a rope vibrating with a standing wave pattern. The nodes and antinodes are labeled on the diagram. When a standing wave pattern is established in a medium, the nodes and the antinodes are always located at the same position along the medium; they are standing still. It is this characteristic that has earned the pattern the name standing wave.
Flickr Physics Photo
A standing wave is established upon a vibrating string using a harmonic oscillator and a frequency generator. A strobe is used to illuminate the string several times during each cycle. The finger is pointing at a nodal position.

Standing Wave Diagrams
The positioning of the nodes and antinodes in a standing wave pattern can be explained by focusing on the interference of the two waves. The nodes are produced at locations where destructive interference occurs. For instance, nodes form at locations where a crest of one wave meets a trough of a second wave; or a half-crest of one wave meets a half-trough of a second wave; or a quarter-crest of one wave meets a quarter-trough of a second wave; etc. Antinodes, on the other hand, are produced at locations where constructive interference occurs. For instance, if a crest of one wave meets a crest of a second wave, a point of large positive displacement results. Similarly, if a trough of one wave meets a trough of a second wave, a point of large negative displacement results. Antinodes are always vibrating back and forth between these points of large positive and large negative displacement; this is because during a complete cycle of vibration, a crest will meet a crest; and then one-half cycle later, a trough will meet a trough. Because antinodes are vibrating back and forth between a large positive and large negative displacement, a diagram of a standing wave is sometimes depicted by drawing the shape of the medium at an instant in time and at an instant one-half vibrational cycle later. This is done in the diagram below.
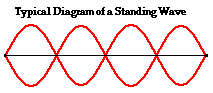
Nodes and antinodes should not be confused with crests and troughs. When the motion of a traveling wave is discussed, it is customary to refer to a point of large maximum displacement as a crest and a point of large negative displacement as a trough. These represent points of the disturbance that travel from one location to another through the medium. An antinode on the other hand is a point on the medium that is staying in the same location. Furthermore, an antinode vibrates back and forth between a large upward and a large downward displacement. And finally, nodes and antinodes are not actually part of a wave. Recall that a standing wave is not actually a wave but rather a pattern that results from the interference of two or more waves. Since a standing wave is not technically a wave, an antinode is not technically a point on a wave. The nodes and antinodes are merely unique points on the medium that make up the wave pattern.

Watch It!
A physics instructor demonstrates and explains the formation of a longitudinal standing wave in a spring.
We Would Like to Suggest ...

Why just read about it and when you could be interacting with it? Interact - that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Standing Wave Patterns Interactive. You can find it in the Physics Interactives section of our website. The
Standing Wave Patterns Interactive provides the learner an environment for exploring the formation of standing waves, standing wave patterns, and mathematical relationships for standing wave patterns.
Check Your Understanding
1. Suppose that there was a ride at an amusement park that was titled The Standing Wave. Which location - node or antinode - on the ride would give the greatest thrill?
2. A standing wave is formed when ____.
a. a wave refracts due to changes in the properties of the medium.
b. a wave reflects off a canyon wall and is heard shortly after it is formed.
c. red, orange, and yellow wavelengths bend around suspended atmospheric particles.
d. two identical waves moving different directions along the same medium interfere.
|
3. The number of nodes in the standing wave shown in the diagram at the right is ____.
|

|
4. The number of antinodes in the standing wave shown in the diagram above right is ____.
Consider the standing wave pattern at the right in answering these next two questions.
|
5. The number of nodes in the entire pattern is ___.
|

|
6. Of all the labeled points, destructive interference occurs at point(s) ____.
|
a. B, C, and D
|
b. A, E, and F
|
c. A only
|
|
d. C only
|
e. all points
|
|