Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 An object placed on a tilted surface will often slide down the surface. The rate at which the object slides down the surface is dependent upon how tilted the surface is; the greater the tilt of the surface, the faster the rate at which the object will slide down it. In physics, a tilted surface is called an inclined plane. Objects are known to accelerate down inclined planes because of an unbalanced force. To understand this type of motion, it is important to analyze the forces acting upon an object on an inclined plane. The diagram at the right depicts the two forces acting upon a crate that is positioned on an inclined plane (assumed to be friction-free). As shown in the diagram, there are always at least two forces acting upon any object that is positioned on an inclined plane - the force of gravity and the normal force. The force of gravity (also known as weight) acts in a downward direction; yet the normal force acts in a direction perpendicular to the surface (in fact, normal means "perpendicular").
An object placed on a tilted surface will often slide down the surface. The rate at which the object slides down the surface is dependent upon how tilted the surface is; the greater the tilt of the surface, the faster the rate at which the object will slide down it. In physics, a tilted surface is called an inclined plane. Objects are known to accelerate down inclined planes because of an unbalanced force. To understand this type of motion, it is important to analyze the forces acting upon an object on an inclined plane. The diagram at the right depicts the two forces acting upon a crate that is positioned on an inclined plane (assumed to be friction-free). As shown in the diagram, there are always at least two forces acting upon any object that is positioned on an inclined plane - the force of gravity and the normal force. The force of gravity (also known as weight) acts in a downward direction; yet the normal force acts in a direction perpendicular to the surface (in fact, normal means "perpendicular").
The Abnormal Normal Force
The first peculiarity of inclined plane problems is that the normal force is not directed in the direction that we are accustomed to. Up to this point in the course, we have always seen normal forces acting in an upward direction, opposite the direction of the force of gravity. But this is only because the objects were always on horizontal surfaces and never upon inclined planes. The truth about normal forces is not that they are always upwards, but rather that they are always directed perpendicular to the surface that the object is on.

The Components of the Gravity Force
The task of determining the net force acting upon an object on an inclined plane is a difficult manner since the two (or more) forces are not directed in opposite directions. Thus, one (or more) of the forces will have to be resolved into perpendicular components so that they can be easily added to the other forces acting upon the object. Usually, any force directed at an angle to the horizontal is resolved into horizontal and vertical components. However, this is not the process that we will pursue with inclined planes. Instead, the process of analyzing the forces acting upon objects on inclined planes will involve resolving the weight vector (Fgrav) into two perpendicular components. This is the second peculiarity of inclined plane problems. The force of gravity will be resolved into two components of force - one directed parallel to the inclined surface and the other directed perpendicular to the inclined surface. The diagram below shows how the force of gravity has been replaced by two components - a parallel and a perpendicular component of force.
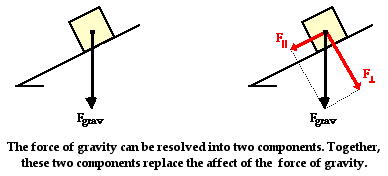
The perpendicular component of the force of gravity is directed opposite the normal force and as such balances the normal force. The parallel component of the force of gravity is not balanced by any other force. This object will subsequently accelerate down the inclined plane due to the presence of an unbalanced force. It is the parallel component of the force of gravity that causes this acceleration. The parallel component of the force of gravity is the net force.
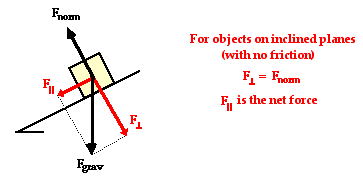
The task of determining the magnitude of the two components of the force of gravity is a mere manner of using the equations. The equations for the parallel and perpendicular components are:

In the absence of friction and other forces (tension, applied, etc.), the acceleration of an object on an incline is the value of the parallel component (m*g*sine of angle) divided by the mass (m). This yields the equation

(in the absence of friction and other forces)
 Simplifying an Inclined Plane Problem
Simplifying an Inclined Plane Problem
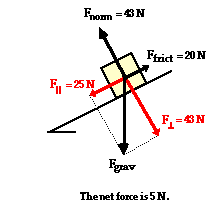
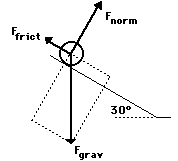
In the presence of friction or other forces (applied force, tensional forces, etc.), the situation is slightly more complicated. Consider the diagram shown at the right. The perpendicular component of force still balances the normal force since objects do not accelerate perpendicular to the incline. Yet the frictional force must also be considered when determining the net force. As in all net force problems, the net force is the vector sum of all the forces. That is, all the individual forces are added together as vectors. The perpendicular component and the normal force add to 0 N. The parallel component and the friction force add together to yield 5 N. The net force is 5 N, directed along the incline towards the floor.
The above problem (and all inclined plane problems) can be simplified through a useful trick known as "tilting the head." An inclined plane problem is in every way like any other net force problem with the sole exception that the surface has been tilted. Thus, to transform the problem back into the form with which you are more comfortable, merely tilt your head in the same direction that the incline was tilted. Or better yet, merely tilt the page of paper (a sure remedy for TNS - "tilted neck syndrome" or "taco neck syndrome") so that the surface no longer appears level. This is illustrated below.
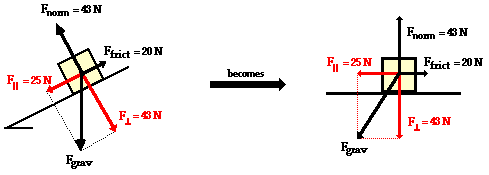
Once the force of gravity has been resolved into its two components and the inclined plane has been tilted, the problem should look very familiar. Merely ignore the force of gravity (since it has been replaced by its two components) and solve for the net force and acceleration.
 As an example consider the situation depicted in the diagram at the right. The free-body diagram shows the forces acting upon a 100-kg crate that is sliding down an inclined plane. The plane is inclined at an angle of 30 degrees. The coefficient of friction between the crate and the incline is 0.3. Determine the net force and acceleration of the crate.
As an example consider the situation depicted in the diagram at the right. The free-body diagram shows the forces acting upon a 100-kg crate that is sliding down an inclined plane. The plane is inclined at an angle of 30 degrees. The coefficient of friction between the crate and the incline is 0.3. Determine the net force and acceleration of the crate.
Begin the above problem by finding the force of gravity acting upon the crate and the components of this force parallel and perpendicular to the incline. The force of gravity is 980 N and the components of this force are Fparallel = 490 N (980 N • sin 30 degrees) and Fperpendicular = 849 N (980 N • cos30 degrees). Now the normal force can be determined to be 849 N (it must balance the perpendicular component of the weight vector). The force of friction can be determined from the value of the normal force and the coefficient of friction; Ffrict is 255 N (Ffrict = "mu"*Fnorm= 0.3 • 849 N). The net force is the vector sum of all the forces. The forces directed perpendicular to the incline balance; the forces directed parallel to the incline do not balance. The net force is 235 N (490 N - 255 N). The acceleration is 2.35 m/s/s (Fnet/m = 235 N/100 kg).
Practice
The two diagrams below depict the free-body diagram for a 1000-kg roller coaster on the first drop of two different roller coaster rides. Use the above principles of vector resolution to determine the net force and acceleration of the roller coaster cars. Assume a negligible effect of friction and air resistance. When done, click the button to view the answers.
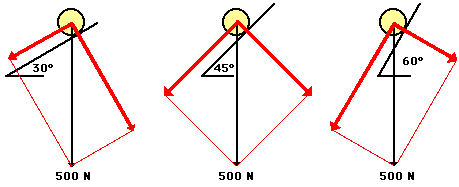
The effects of the incline angle on the acceleration of a roller coaster (or any object on an incline) can be observed in the two practice problems above. As the angle is increased, the acceleration of the object is increased. The explanation of this relates to the components that we have been drawing. As the angle increases, the component of force parallel to the incline increases and the component of force perpendicular to the incline decreases. It is the parallel component of the weight vector that causes the acceleration. Thus, accelerations are greater at greater angles of incline. The diagram below depicts this relationship for three different angles of increasing magnitude.
 Some Roller Coaster Physics
Some Roller Coaster Physics
Roller coasters produce two thrills associated with the initial drop down a steep incline. The thrill of acceleration is produced by using large angles of incline on the first drop; such large angles increase the value of the parallel component of the weight vector (the component that causes acceleration). The thrill of weightlessness is produced by reducing the magnitude of the normal force to values less than their usual values. It is important to recognize that the thrill of weightlessness is a feeling associated with a lower than usual normal force. Typically, a person weighing 700 N will experience a 700 N normal force when sitting in a chair. However, if the chair is accelerating down a 60-degrees incline, then the person will experience a 350 Newton normal force. This value is less than normal and contributes to the feeling of weighing less than one's normal weight - i.e., weightlessness.
More Practice
Use the widget below to investigate other inclined plane situations. Simply enter the mass, the incline angle and the coefficient of friction (use 0 for frictionless situations). Then click the Submit button to view the acceleration.
Check Your Understanding
The following questions are intended to test your understanding of the mathematics and concepts of inclined planes. Once you have answered the question, click the button to see the answers.
1. Two boys are playing ice hockey on a neighborhood street. A stray puck travels across the friction-free ice and then up the friction-free incline of a driveway. Which one of the following ticker tapes (A, B, or C) accurately portrays the motion of the puck as it travels across the level street and then up the driveway?

Explain your answer.
2. Little Johnny stands at the bottom of the driveway and kicks a soccer ball. The ball rolls northward up the driveway and then rolls back to Johnny. Which one of the following velocity-time graphs (A, B, C, or D) most accurately portrays the motion of the ball as it rolls up the driveway and back down?
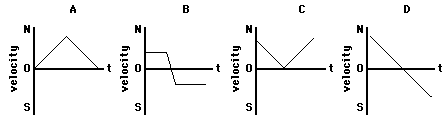
Explain your answer.
3. A golf ball is rolling across a horizontal section of the green on the 18th hole. It then encounters a steep downward incline (see diagram). Friction is involved. Which of the following ticker tape patterns (A, B, or C) might be an appropriate representation of the ball's motion?
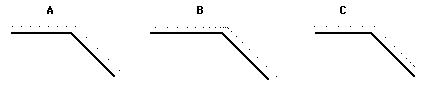
Explain why the inappropriate patterns are inappropriate.
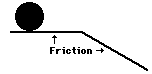 4. Missy dePenn's eighth frame in the Wednesday night bowling league was a disaster. The ball rolled off the lane, passed through the freight door in the building's rear, and then down the driveway. Millie Meater (Missy's teammate), who was spending every free moment studying for her physics test, began visualizing the velocity-time graph for the ball's motion. Which one of the velocity-time graphs (A, B, C, or D) would be an appropriate representation of the ball's motion as it rolls across the horizontal surface and then down the incline? Consider frictional forces.
4. Missy dePenn's eighth frame in the Wednesday night bowling league was a disaster. The ball rolled off the lane, passed through the freight door in the building's rear, and then down the driveway. Millie Meater (Missy's teammate), who was spending every free moment studying for her physics test, began visualizing the velocity-time graph for the ball's motion. Which one of the velocity-time graphs (A, B, C, or D) would be an appropriate representation of the ball's motion as it rolls across the horizontal surface and then down the incline? Consider frictional forces.
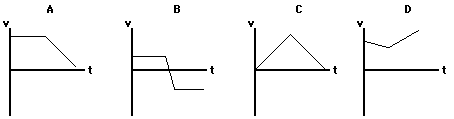
5. Three lab partners - Olive N. Glenveau, Glen Brook, and Warren Peace - are discussing an incline problem (see diagram). They are debating the value of the normal force. Olive claims that the normal force is 250 N; Glen claims that the normal force is 433 N; and Warren claims that the normal force is 500 N. While all three answers seem reasonable, only one is correct. Indicate which two answers are wrong and explain why they are wrong.

 6. Lon Scaper is doing some lawn work when a 2-kg tire escapes from his wheelbarrow and begins rolling down a steep hill (a 30° incline) in San Francisco. Sketch the parallel and perpendicular components of this weight vector. Determine the magnitude of the components using trigonometric functions. Then determine the acceleration of the tire. Ignore resistance force.
6. Lon Scaper is doing some lawn work when a 2-kg tire escapes from his wheelbarrow and begins rolling down a steep hill (a 30° incline) in San Francisco. Sketch the parallel and perpendicular components of this weight vector. Determine the magnitude of the components using trigonometric functions. Then determine the acceleration of the tire. Ignore resistance force.
Finally, determine which one of the velocity-time graph would represent the motion of the tire as it rolls down the incline.
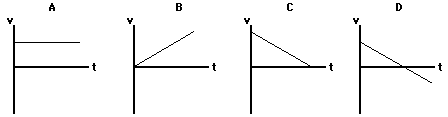
Explain your answer.
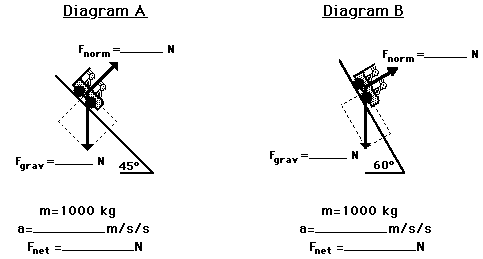
7. In each of the following diagrams, a 100-kg box is sliding down a frictional surface at a constant speed of 0.2 m/s. The incline angle is different in each situation. Analyze each diagram and fill in the blanks.
Diagram A

Diagram B