Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
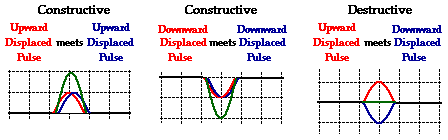
Wave interference is the phenomenon that occurs when two waves meet while traveling along the same medium. The interference of waves causes the medium to take on a shape that results from the net effect of the two individual waves upon the particles of the medium. As mentioned in a previous unit of The Physics Classroom Tutorial, if two upward displaced pulses having the same shape meet up with one another while traveling in opposite directions along a medium, the medium will take on the shape of an upward displaced pulse with twice the amplitude of the two interfering pulses. This type of interference is known as constructive interference. If an upward displaced pulse and a downward displaced pulse having the same shape meet up with one another while traveling in opposite directions along a medium, the two pulses will cancel each other's effect upon the displacement of the medium and the medium will assume the equilibrium position. This type of interference is known as destructive interference. The diagrams below show two waves - one is blue and the other is red - interfering in such a way to produce a resultant shape in a medium; the resultant is shown in green. In two cases (on the left and in the middle), constructive interference occurs and in the third case (on the far right, destructive interference occurs.
But how can sound waves that do not possess upward and downward displacements interfere constructively and destructively? Sound is a pressure wave that consists of compressions and rarefactions. As a compression passes through a section of a medium, it tends to pull particles together into a small region of space, thus creating a high-pressure region. And as a rarefaction passes through a section of a medium, it tends to push particles apart, thus creating a low-pressure region. The interference of sound waves causes the particles of the medium to behave in a manner that reflects the net effect of the two individual waves upon the particles. For example, if a compression (high pressure) of one wave meets up with a compression (high pressure) of a second wave at the same location in the medium, then the net effect is that that particular location will experience an even greater pressure. This is a form of constructive interference. If two rarefactions (two low-pressure disturbances) from two different sound waves meet up at the same location, then the net effect is that that particular location will experience an even lower pressure. This is also an example of constructive interference. Now if a particular location along the medium repeatedly experiences the interference of two compressions followed up by the interference of two rarefactions, then the two sound waves will continually reinforce each other and produce a very loud sound. The loudness of the sound is the result of the particles at that location of the medium undergoing oscillations from very high to very low pressures. As mentioned in a previous unit, locations along the medium where constructive interference continually occurs are known as anti-nodes. The animation below shows two sound waves interfering constructively in order to produce very large oscillations in pressure at a variety of anti-nodal locations. Note that compressions are labeled with a C and rarefactions are labeled with an R.

Now if two sound waves interfere at a given location in such a way that the compression of one wave meets up with the rarefaction of a second wave, destructive interference results. The net effect of a compression (which pushes particles together) and a rarefaction (which pulls particles apart) upon the particles in a given region of the medium is to not even cause a displacement of the particles. The tendency of the compression to push particles together is canceled by the tendency of the rarefactions to pull particles apart; the particles would remain at their rest position as though there wasn't even a disturbance passing through them. This is a form of destructive interference. Now if a particular location along the medium repeatedly experiences the interference of a compression and rarefaction followed up by the interference of a rarefaction and a compression, then the two sound waves will continually cancel each other and no sound is heard. The absence of sound is the result of the particles remaining at rest and behaving as though there were no disturbance passing through it. Amazingly, in a situation such as this, two sound waves would combine to produce no sound. As mentioned in a previous unit, locations along the medium where destructive interference continually occurs are known as nodes.
Two Source Sound Interference
A popular Physics demonstration involves the interference of two sound waves from two speakers. The speakers are set approximately 1-meter apart and produced identical tones. The two sound waves traveled through the air in front of the speakers, spreading out through the room in spherical fashion. A snapshot in time of the appearance of these waves is shown in the diagram below. In the diagram, the compressions of a wavefront are represented by a thick line and the rarefactions are represented by thin lines. These two waves interfere in such a manner as to produce locations of some loud sounds and other locations of no sound. Of course the loud sounds are heard at locations where compressions meet compressions or rarefactions meet rarefactions and the "no sound" locations appear wherever the compressions of one of the waves meet the rarefactions of the other wave. If you were to plug one ear and turn the other ear towards the place of the speakers and then slowly walk across the room parallel to the plane of the speakers, then you would encounter an amazing phenomenon. You would alternatively hear loud sounds as you approached anti-nodal locations and virtually no sound as you approached nodal locations. (As would commonly be observed, the nodal locations are not true nodal locations due to reflections of sound waves off the walls. These reflections tend to fill the entire room with reflected sound. Even though the sound waves that reach the nodal locations directly from the speakers destructively interfere, other waves reflecting off the walls tend to reach that same location to produce a pressure disturbance.)
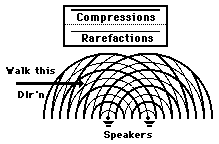

Destructive interference of sound waves becomes an important issue in the design of concert halls and auditoriums. The rooms must be designed in such as way as to reduce the amount of destructive interference. Interference can occur as the result of sound from two speakers meeting at the same location as well as the result of sound from a speaker meeting with sound reflected off the walls and ceilings. If the sound arrives at a given location such that compressions meet rarefactions, then destructive interference will occur resulting in a reduction in the loudness of the sound at that location. One means of reducing the severity of destructive interference is by the design of walls, ceilings, and baffles that serve to absorb sound rather than reflect it. This will be discussed in more detail later in Lesson 3.
The destructive interference of sound waves can also be used advantageously in noise reduction systems. Earphones have been produced that can be used by factory and construction workers to reduce the noise levels on their jobs. Such earphones capture sound from the environment and use computer technology to produce a second sound wave that one-half cycle out of phase. The combination of these two sound waves within the headset will result in destructive interference and thus reduce a worker's exposure to loud noise.
Musical Beats and Intervals
Interference of sound waves has widespread applications in the world of music. Music seldom consists of sound waves of a single frequency played continuously. Few music enthusiasts would be impressed by an orchestra that played music consisting of the note with a pure tone played by all instruments in the orchestra. Hearing a sound wave of 256 Hz (middle C) would become rather monotonous (both literally and figuratively). Rather, instruments are known to produce overtones when played resulting in a sound that consists of a multiple of frequencies. Such instruments are described as being rich in tone color. And even the best choirs will earn their money when two singers sing two notes (i.e., produce two sound waves) that are an octave apart. Music is a mixture of sound waves that typically have whole number ratios between the frequencies associated with their notes. In fact, the major distinction between music and noise is that noise consists of a mixture of frequencies whose mathematical relationship to one another is not readily discernible. On the other hand, music consists of a mixture of frequencies that have a clear mathematical relationship between them. While it may be true that "one person's music is another person's noise" (e.g., your music might be thought of by your parents as being noise), a physical analysis of musical sounds reveals a mixture of sound waves that are mathematically related.
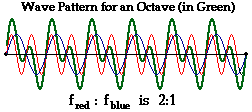
To demonstrate this nature of music, let's consider one of the simplest mixtures of two different sound waves - two sound waves with a 2:1 frequency ratio. This combination of waves is known as an octave. A simple sinusoidal plot of the wave pattern for two such waves is shown below. Note that the red wave has two times the frequency of the blue wave. Also observe that the interference of these two waves produces a resultant (in green) that has a periodic and repeating pattern. One might say that two sound waves that have a clear whole number ratio between their frequencies interfere to produce a wave with a regular and repeating pattern. The result is music.
Another simple example of two sound waves with a clear mathematical relationship between frequencies is shown below. Note that the red wave has three-halves the frequency of the blue wave. In the music world, such waves are said to be a fifth apart and represent a popular musical interval. Observe once more that the interference of these two waves produces a resultant (in green) that has a periodic and repeating pattern. It should be said again: two sound waves that have a clear whole number ratio between their frequencies interfere to produce a wave with a regular and repeating pattern; the result is music.

Finally, the diagram below illustrates the wave pattern produced by two dissonant or displeasing sounds. The diagram shows two waves interfering, but this time there is no simple mathematical relationship between their frequencies (in computer terms, one has a wavelength of 37 and the other has a wavelength 20 pixels). Observe (look carefully) that the pattern of the resultant is neither periodic nor repeating (at least not in the short sample of time that is shown). The message is clear: if two sound waves that have no simple mathematical relationship between their frequencies interfere to produce a wave, the result will be an irregular and non-repeating pattern. This tends to be displeasing to the ear.

The widget below allows you to add two waves together and view the resulting waveform. Wave 1 has a frequency of 2.00 Hz. Wave 2's frequency canbe selected from the pull-down menu. Experiment with various Wave 2 frequencies and observe the waveform that results from their interference.
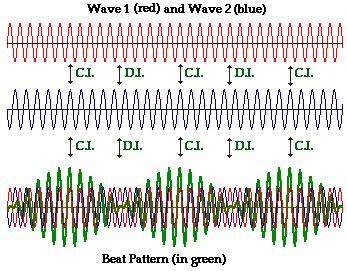
A final application of physics to the world of music pertains to the topic of beats. Beats are the periodic and repeating fluctuations heard in the intensity of a sound when two sound waves of very similar frequencies interfere with one another. The diagram below illustrates the wave interference pattern resulting from two waves (drawn in red and blue) with very similar frequencies. A beat pattern is characterized by a wave whose amplitude is changing at a regular rate. Observe that the beat pattern (drawn in green) repeatedly oscillates from zero amplitude to a large amplitude, back to zero amplitude throughout the pattern. Points of constructive interference (C.I.) and destructive interference (D.I.) are labeled on the diagram. When constructive interference occurs between two crests or two troughs, a loud sound is heard. This corresponds to a peak on the beat pattern (drawn in green). When destructive interference between a crest and a trough occurs, no sound is heard; this corresponds to a point of no displacement on the beat pattern. Since there is a clear relationship between the amplitude and the loudness, this beat pattern would be consistent with a wave that varies in volume at a regular rate.
Beat Frequency
The beat frequency refers to the rate at which the volume is heard to be oscillating from high to low volume. For example, if two complete cycles of high and low volumes are heard every second, the beat frequency is 2 Hz. The beat frequency is always equal to the difference in frequency of the two notes that interfere to produce the beats. So if two sound waves with frequencies of 256 Hz and 254 Hz are played simultaneously, a beat frequency of 2 Hz will be detected. A common physics demonstration involves producing beats using two tuning forks with very similar frequencies. If a tine on one of two identical tuning forks is wrapped with a rubber band, then that tuning forks frequency will be lowered. If both tuning forks are vibrated together, then they produce sounds with slightly different frequencies. These sounds will interfere to produce detectable beats. The human ear is capable of detecting beats with frequencies of 7 Hz and below.
A piano tuner frequently utilizes the phenomenon of beats to tune a piano string. She will pluck the string and tap a tuning fork at the same time. If the two sound sources - the piano string and the tuning fork - produce detectable beats then their frequencies are not identical. She will then adjust the tension of the piano string and repeat the process until the beats can no longer be heard. As the piano string becomes more in tune with the tuning fork, the beat frequency will be reduced and approach 0 Hz. When beats are no longer heard, the piano string is tuned to the tuning fork; that is, they play the same frequency. The process allows a piano tuner to match the strings' frequency to the frequency of a standardized set of tuning forks.
The widget below allows you to investigate the effect of the frequencies of two intefering waves upon the beat pattern. The frequency of the first wave is fixed at 50 Hz. You can set the frequency of the second wave using the pull-down menu. How does the difference in frequency of the two waves affect the beat pattern?
Important Note: Many of the diagrams on this page represent a sound wave by a sine wave. Such a wave more closely resembles a transverse wave and may mislead people into thinking that sound is a transverse wave. Sound is not a transverse wave, but rather a longitudinal wave. Nonetheless, the variations in pressure with time take on the pattern of a sine wave and thus a sine wave is often used to represent the pressure-time features of a sound wave.
We Would Like to Suggest ...

Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our Beats Interactive. The Interactive is found in the Physics Interactives section of our website and allows a learner to alter the frequency of a pair of tuning forks and view the interference pattern that results from their interference.
Check Your Understanding
Two speakers are arranged so that sound waves with the same frequency are produced and radiate through the room. An interference pattern is created (as represented in the diagram at the right). The thick lines in the diagram represent wave crests and the thin lines represent wave troughs. Use the diagram to answer the next two questions.
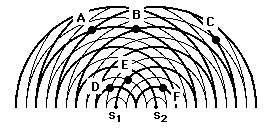 1. At which of the labeled point(s) would constructive interference occur?
1. At which of the labeled point(s) would constructive interference occur?
a. B only
b. A, B, and C
c. D, E, and F
d. A and B
2. How many of the six labeled points represent anti-nodes?
3. A tuning fork with a frequency of 440 Hz is played simultaneously with a fork with a frequency of 437 Hz. How many beats will be heard over a period of 10 seconds?
4. Why don't we hear beats when different keys on the piano are played at the same time?