Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 A common Physics lab is to sight through the long side of an isosceles triangle at a pin or other object held behind the opposite face. When done so, an unusual observation - a discrepant event - is observed. The diagram on the left below depicts the physical situation. A ray of light entered the face of the triangular block at a right angle to the boundary. This ray of light passes across the boundary without refraction since it was incident along the normal (recall the If I Were An Archer Fish page). The ray of light then travels in a straight line through the glass until it reaches the second boundary. Now instead of transmitting across this boundary, all of the light seems to reflect off the boundary and transmit out the opposite face of the isosceles triangle. This discrepant event bothers many as they spend several minutes looking for the light to refract through the second boundary. Then finally, to their amazement, they looked through the third face of the block and clearly see the ray. What happened? Why did light not refract through the second face?
A common Physics lab is to sight through the long side of an isosceles triangle at a pin or other object held behind the opposite face. When done so, an unusual observation - a discrepant event - is observed. The diagram on the left below depicts the physical situation. A ray of light entered the face of the triangular block at a right angle to the boundary. This ray of light passes across the boundary without refraction since it was incident along the normal (recall the If I Were An Archer Fish page). The ray of light then travels in a straight line through the glass until it reaches the second boundary. Now instead of transmitting across this boundary, all of the light seems to reflect off the boundary and transmit out the opposite face of the isosceles triangle. This discrepant event bothers many as they spend several minutes looking for the light to refract through the second boundary. Then finally, to their amazement, they looked through the third face of the block and clearly see the ray. What happened? Why did light not refract through the second face?
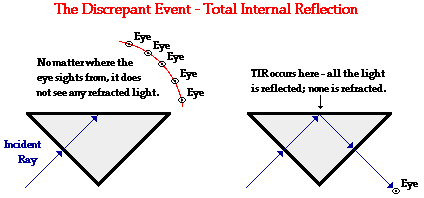
The phenomenon observed in this part of the lab is known as total internal reflection. Total internal reflection, or TIR as it is intimately called, is the reflection of the total amount of incident light at the boundary between two media. TIR is the topic of focus in Lesson 3.
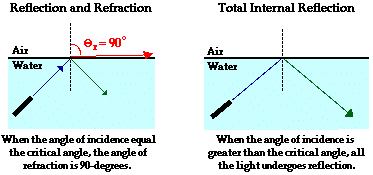
To understand total internal reflection, we will begin with a thought experiment. Suppose that a laser beam is submerged in a tank of water (don't do this at home) and pointed upwards towards water-air boundary. Then suppose that the angle at which the beam is directed upwards is slowly altered, beginning with small angles of incidence and proceeding towards larger and larger angles of incidence. What would be observed in such an experiment? If we understand the principles of boundary behavior, we would expect that we would observe both reflection and refraction. And indeed, that is what is observed (mostly). But that's not the only observation that we could make. We would also observe that the intensity of the reflected and refracted rays do not remain constant. At angle of incidence close to 0 degrees, most of the light energy is transmitted across the boundary and very little of it is reflected. As the angle is increased to greater and greater angles, we would begin to observe less refraction and more reflection. That is, as the angle of incidence is increased, the brightness of the refracted ray decreases and the brightness of the reflected ray increases. Finally, we would observe that the angles of the reflection and refraction are not equal. Since the light waves would refract away from the normal (a case of the SFA principle of refraction), the angle of refraction would be greater than the angle of incidence. And if this were the case, the angle of refraction would also be greater than the angle of reflection (since the angles of reflection and incidence are the same). As the angle of incidence is increased, the angle of refraction would eventually reach a 90-degree angle. These principles are depicted in the diagram below.
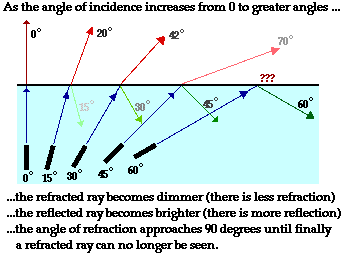
The maximum possible angle of refraction is 90-degrees. If you think about it (a practice that always helps), you recognize that if the angle of refraction were greater than 90 degrees, then the refracted ray would lie on the incident side of the medium - that's just not possible. So in the case of the laser beam in the water, there is some specific value for the angle of incidence (we'll call it the critical angle) that yields an angle of refraction of 90-degrees. This particular value for the angle of incidence could be calculated using Snell's Law (ni = 1.33, nr = 1.000, 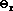 = 90 degrees,
= 90 degrees, 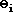 = ???) and would be found to be 48.6 degrees. Any angle of incidence that is greater than 48.6 degrees would not result in refraction. Instead, when the angles of incidence is greater than 48.6 degrees (the critical angle), all of the energy (the total energy) carried by the incident wave to the boundary stays within the water (internal to the original medium) and undergoes reflection off the boundary. When this happens, total internal reflection occurs.
= ???) and would be found to be 48.6 degrees. Any angle of incidence that is greater than 48.6 degrees would not result in refraction. Instead, when the angles of incidence is greater than 48.6 degrees (the critical angle), all of the energy (the total energy) carried by the incident wave to the boundary stays within the water (internal to the original medium) and undergoes reflection off the boundary. When this happens, total internal reflection occurs.
Two Requirements for Total Internal Reflection
Total internal reflection (TIR) is the phenomenon that involves the reflection of all the incident light off the boundary. TIR only takes place when both of the following two conditions are met:
- the light is in the more dense medium and approaching the less dense medium.
- the angle of incidence is greater than the so-called critical angle.
Total internal reflection will not take place unless the incident light is traveling within the more optically dense medium towards the less optically dense medium. TIR will happen for light traveling from water towards air, but it will not happen for light traveling from air towards water. TIR would happen for light traveling from water towards air, but it will not happen for light traveling from water (n=1.333) towards crown glass (n=1.52). TIR occurs because the angle of refraction reaches a 90-degree angle before the angle of incidence reaches a 90-degree angle. The only way for the angle of refraction to be greater than the angle of incidence is for light to bend away from the normal. Since light only bends away from the normal when passing from a more dense medium into a less dense medium, then this would be a necessary condition for total internal reflection.
Total internal reflection only occurs with large angles of incidence. Question: How large is large? Answer: larger than the critical angle. As mentioned above, the critical angle for the water-air boundary is 48.6 degrees. So for angles of incidence greater than 48.6-degrees, TIR occurs. But 48.6 degrees is the critical angle only for the water-air boundary. The actual value of the critical angle is dependent upon the two materials on either side of the boundary. For the crown glass-air boundary, the critical angle is 41.1 degrees. For the diamond-air boundary, the critical angle is 24.4 degrees. For the diamond-water boundary, the critical angle is 33.4 degrees. The critical angle is different for different media. In the next part of Lesson 3, we will investigate how to determine the critical angle for any two materials. For now, let's internalize the idea that TIR can only occur if the angle of incidence is greater than the critical angle for the particular combination of materials.
 Light Piping and Optical Fibers
Light Piping and Optical Fibers
Total internal reflection is often demonstrated in a Physics class through a variety of demonstrations. In one such demonstration, a beam of laser light is directed into a coiled plastic thing-a-ma jig. The plastic served as a light pipe, directing the light through the coils until it finally exits out the opposite end. Once the light entered the plastic, it was in the more dense medium. Every time the light approached the plastic-air boundary, it is approaching at angles greater than the critical angle. The two conditions necessary for TIR are met, and all of the incident light at the plastic-air boundary stays internal to the plastic and undergoes reflection. And with the room lights off, every student becomes quickly aware of the ancient truth that Physics is better than drugs.
This demonstration helps to illustrate the principle by which optical fibers work. The use of a long strand of plastic (or other material such as glass) to pipe light from one end of the medium to the other is the basis for modern day use of optical fibers. Optical fibers are used in communication systems and micro-surgeries. Since total internal reflection takes place within the fibers, no incident energy is ever lost due to the transmission of light across the boundary. The intensity of the signal remains constant.
 Another common Physics demonstration involves the use of a large jug filled with water and a laser beam. The jug has a pea-sized hole drilled in its side such that when the cork is removed from the top of the jug, water begins to stream out the jug's side. The beam of laser light is then directed into the jug from the opposite side of the hole, through the water and into the falling stream. The laser light exits the jug through the hole but is still in the water. As the stream of water begins to fall as a projectile along a parabolic path to the ground, the laser light becomes trapped within the water due to total internal reflection. Being in the more dense medium (water) and heading towards a boundary with a less dense medium (air), and being at angles of incidence greater than the critical angle, the light never leaves the stream of water. In fact, the stream of water acts as a light pipe to pipe the laser beam along its trajectory. Once more, students viewing the demonstration are convinced of the fact that Physics is better than drugs.
Another common Physics demonstration involves the use of a large jug filled with water and a laser beam. The jug has a pea-sized hole drilled in its side such that when the cork is removed from the top of the jug, water begins to stream out the jug's side. The beam of laser light is then directed into the jug from the opposite side of the hole, through the water and into the falling stream. The laser light exits the jug through the hole but is still in the water. As the stream of water begins to fall as a projectile along a parabolic path to the ground, the laser light becomes trapped within the water due to total internal reflection. Being in the more dense medium (water) and heading towards a boundary with a less dense medium (air), and being at angles of incidence greater than the critical angle, the light never leaves the stream of water. In fact, the stream of water acts as a light pipe to pipe the laser beam along its trajectory. Once more, students viewing the demonstration are convinced of the fact that Physics is better than drugs.
Flickr Physics Photo
Laser light shown passing into a hemi-cylindrical dish filled with water. The light enters the water (at the curved side of the dish) along the normal line; no bending occurs upon entry. The light continues through the water along a straight line until it reaches the boundary with air (at the flat side of the dish). The angle of incidence in the water is 50°. Since the angle of incidence is greater the air-water critical angle of about 48°, it undergoes total internal reflection (TIR). Rather than refract out of the dish of water at the flat side, the laser light is seen reflecting and exiting along the curved side of the dish.

We Would Like to Suggest ...

Why just read about it and when you could be interacting with it? Interact - that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Refraction Interactive. You can find it in the Physics Interactives section of our website. The
Refraction Interactive provides the learner an interactive enivronment for exploring the refraction and reflection of light at a boundary between two materials.
Check Your Understanding
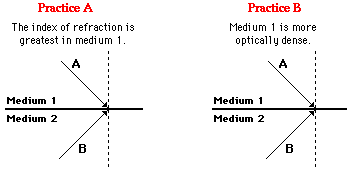
1. For each combination of media, which light ray (A or B) will undergo total internal reflection if the incident angle is gradually increased?