Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Previously in this lesson, we learned that two-dimensional collisions involve the conserving of momentum in both the x- and the y-directions. Whatever east-west momentum that was present in the system before the collision is equal to the east-west momentum after the collision, Similarly, whatever north-south momentum that was present in the system before the collision is equal to the amount of north-south momentum in the system after the collision. System momentum is conserved in both dimensions.
To illustrate the point, we considered the collision of two football players in mid-air. Player A had eastward momentum and Player B had southward momentum before the collision, After the collision, the two players move together in the same direction at the same speed - a type of collision known as a hit-and-stick collision.
In our discussion on the previous page, we learned that the total system momentum in the eastward direction before the collision was equal to the total system momentum in the eastward direction after the collision. This eastward momentum is possessed only by Player A before the collision but shared by both players after the collision. Similarly, the total system momentum in the southward direction before the collision is equal to the total system momentum in the southward direction after the collision. This southward momentum was possessed only by Player B before the collision but shared by both players after the collision.
Among the questions we will now ponder in this part of Lesson 3 is how can we use momentum conservation in two dimensions in order to determine the post-collision velocity (magnitude and direction) of the two colliding objects?
Momentum Conservation and The Pythagorean Theorem
Momentum is a vector quantity. And all the operations that apply to vector quantities apply to momentum. Momentum vectors can be added like any two vectors. And momentum vectors can be resolved into components like any vector. The rules of vector addition and vector resolution apply to momentum. And when analyzing two-dimensional collisions using the law of momentum conservation, vector addition and vector resolution will be two tools from your Physics toolbox that you will frequently use.
On this page of Lesson 3, we are considering hit-and-stick, right-angle collisions between two objects. We know that total system momentum is conserved; that's the law of momentum conservation. When we apply the law to a two-dimensional collision, we apply it twice - once for the x-dimension and once for the y-dimension. We see that in the diagram above. The system of two players possessed 400 kg•m/s of eastward momentum before the collision. And so the two entangled players (the system) possesses 400 kg•m/s of eastward momentum after the collision. Similarly, there are 300 kg•m/s of southward momentum before the collision and 300 kg•m/s of southward momentum after the collision. Because the eastward and southward momentum components are at right angles to one another, the vector sum can be determined using the Pythagorean theorem. The total system momentum - ptotal - is determined by adding the two right-angle vectors. The result is that the total system momentum is 500 kg•m/s.
 You Try it Now!
You Try it Now!
Let's try a second example. Suppose Ima Rilla Saari becomes careless one winter morning in the school parking lot. She's driving her car northward across parking lanes with a momentum of 2000 kg•m/s. Meanwhile, Ben Abaday is pre-occupied by thoughts of his Period 1 math class as he drives his car westward through the parking lanes with a momentum of 1500 kg•m/s. The two cars collide, entangle, and slide across the ice after the collision. Use the law of momentum conservation and the Pythagorean theorem to determine the total system momentum of the two cars ... both before and immediately after the collision. When you're ready, tap the See Answer button to see how you did.
The Direction of the ptotal Vector
The post-collision direction of the two entangled objects in a hit-and-stick, right-angle collision can be predicted from the knowledge of the pre-collision momentum of the individual objects. For hit-and-stick, right-angle collisions, the initial momentum vectors of the two objects are at right angles to one another. When added as vectors to determine the total system momentum, these individual object momentum vectors are the legs of a right triangle. A sine, cosine, or tangent function can be used to determine the angles within the right triangle. From such angles, we can determine the direction of the momentum vector. This direction is equivalent to the direction the entangled objects move after the collision. Let's see how it works for our football player collision - Player A (pinitial = 400 kg•m/s, East) colliding with Player B (pinitial = 300 kg•m/s, South).
The diagram below shows the two individual object momentum vectors being added in head-to-tail fashion. The hypotenuse of this triangle is a vector representing the total momentum of the system of two players. The angle theta (θ) is marked at the tail of this ptotal vector. (Always mark the angle at the tail of the total momentum vector.) The tangent of this angle theta relates the ratio of the lengths of the side opposite to theta to the side adjacent theta. The 300 kg•m/s is the side opposite of the angle theta and the 400 kg•m/s is the side that is adjacent to the angle theta. And so tangent of theta is equal to the ratio of 300 to 400. This is shown in the diagram on the right side. We wish to determine the value of the angle theta so that we can identify the direction of the ptotal vector. The algebra is shown on the right side of the graphic. The result of the calculation is that theta is 36.9°.
The value of 36.9° represents theta - an angle inside of the right triangle. But this is not the direction. You will need to turn on your noodle (that's your brain) and take the reasoning one step further in order to express the direction of the ptotal vector. One way to express the direction is to simply say that ptotal vector is 36.9° south of east. That will suffice for most Physics classes and it is indeed accurate. But the more common convention for direction is the counter clockwise from east convention (Review the CCW convention).
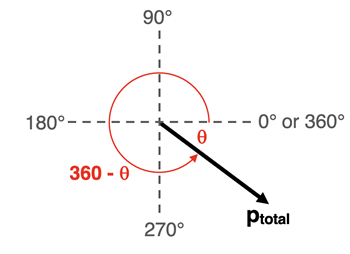
The CCW convention imagines a vector as having been rotated about its tail in the counter-clockwise direction beginning at East by some angle; the direction is that rotation angle. We will need to use the 36.9° to determine the CCW rotation angle. The ptotal vector is in the fourth quadrant and is thus has been rotated counterclockwise from east by an angle somewhere in between 270.0° and 360.0°. A rotation of a vector by 360.0° returns the vector to the due East direction. But this ptotal vector has not been rotated that far. It is short of a full 360.0° rotation by an amount of 36.9°. And so the CCW direction of the ptotal vector is ...
CCW Direction = 360.0° - 36.9°
CCW Direction = 323.1°
Since the momentum vectors always point in the direction of the object's motion, the direction of this ptotal vector is the direction that the objects move after the collision.
The method of determining that the objects move in a hit-and-stick, right-angle collision can be determined by following these steps:
- Identify the magnitude and direction of the pre-collision momentum vectors of the two colliding objects.
- Construct a diagram showing how these two vectors add together to produce the momentum vector of the system (ptotal). Help yourself (and others) out by putting some labels on the diagram - for instance, pA, pB, and ptotal.
- Label theta on the diagram. Theta (θ) is an angle inside the triangle between the ptotal vector and either the x-axis or the y-axis.
- Use a trigonometric function to determine the value of theta. Write it down. (But don't stop ... you're not done.)
- Use your diagram to make identify the direction of your ptotal vector. Use the CCW convention to be safe. Recall that east is 0°, north is 90°, west is 180°, and south is 270°. It helps to first determine the range of possible answers (for instance, between 180° and 270°) and then to use your noodle to determine the specific answer within that range. A good diagram is essential if you are struggling with this!
 Practice Makes Perfect
Practice Makes Perfect
It's your turn to try it now. Determine the post-collision direction of the two entangled cars from our previous example - Ima Rilla Saari (2000 kg•m/s, north) colliding with Ben Abaday (1500 kg•m/s, west). Use the method above. This method relies on the use of a good diagram; don't skip that part. When you're ready, tap the See Answer button to see how you did.
Determining a Post-Collision Velocity
We have just learned how to determine the direction of the post-collision momentum vector. This direction is equivalent to the direction of the objects' post-collision velocity. Now we will learn how to determine the magnitude of the objects' post-collision velocity. The velocity is related to the momentum by the equation p = m•v. The Pythagorean theorem allows us to determine the post-collision momentum of the two entangled objects. Determining the velocity with which they move is possible if we know the combined mass of these two objects (mtotal). Once known, the velocity is calculated by substituting ptotal and mtotal into the p = m•v equation. For a problem in which pre-collision information is provided (momentum and masses of the individual objects), the following method can be used to determine the post-collision velocity.
- Identify (or calculate) the momentum (magnitude and direction) of the two individual objects before the collision.
- Use a vector addition diagram and Pythagorean theorem to calculate the total system momentum (ptotal) before the collision. Since momentum is conserved, this total system momentum value is also the ptotal for after the collision.
- Determine the total mass of the system (mtotal) by adding the masses of the individual objects.
- Calculate the velocity of the combined objects using v = ptotal / mtotal. Since each object moves together at the same speed, this calculation provides the magnitude of the velocity of both of the objects after the collision.
Example 1
As a first example, let's consider the football player collision that we have been discussing. We are going to give it a slight twist.
Player A has a mass of 80.0 kg and is moving east with a velocity of 5.0 m/s. Player B has a mass of 60.0 kg and is moving south with a velocity of 5.0 m/s. The two players collide and move together at the same speed after the collision. Determine the post-collision velocity of the two players.
The slight twist is that the momentum values are not given. Instead the mass and velocity values are given.
The solution begins by using the p=m•v equation to calculate the momentum of the two individual players before the collision:
Player A: p = m•v = (80.0 kg)•(5.0 m/s) = 400 kg•m/s, East
Player B: p = m•v = (60.0 kg)•(5.0 m/s) = 300 kg•m/s, South
Now a vector addition diagram can be drawn and the total momentum of the system before the collision can be calculated using the Pythagorean theorem. If you haven't noticed yet, this is the same problem with the same momentum values that we've been analyzing throughout this lesson. The work is re-shown below.
The total momentum of the system before the collision is equal to the total momentum of the system after the collision. The ptotal is 500 kg•m/s. The total mass (mtotal) of these two players is 80.0 kg + 60.0 kg or 140.0 kg. Now we can use the total momentum and the total mass to calculate the after-collision velocity value of each of the objects.
v = ptotal / mtotal = (500 kg•m/s) / (140.0 kg)
v = 3.57 m/s
Example 2
Ima Rilla Saari is driving her 1000-kg car northward across lanes of the parking lot with a speed of 2.0 m/s. Ben Abaday is driving his 1000-kg car westward with a speed of 1.5 m/s. The two cars collide, entangle, and travel together across the ice at the same speed. Determine the magnitude of the post-collision velocity of the two cars.
Let's begin by using the p=m•v equation to calculate the momentum of the two individual cars before the collision:
Ima's Car: p = m•v = (1000 kg)•(3.0 m/s) = 2000 kg•m/s, North
Ben's Car: p = m•v = (1000 kg)•(1.5 m/s) = 1500 kg•m/s, West
Now let's construct a vector addition diagram and calculate the total momentum of the system before the collision using the Pythagorean theorem.
The total momentum of the system before the collision is equal to the total momentum of the system after the collision. The ptotal is 2500 kg•m/s. The total mass (mtotal) of these two players is 1000 kg + 1000 kg or 2000 kg. Now we can use the total momentum and the total mass to calculate the after-collision velocity value of each of the objects.
v = ptotal / mtotal = (2500 kg•m/s) / (2000 kg)
v = 1.25 m/s
Example 3
Jillian and Elissa are in the bumper car rink at the amusement park. Jillian and her car have a combined mass of 185 kg. She is driving south at 1.45 m/s. Elissa and her car have a combined mass of 205 kg. She is driving west at 1.75 m/s. The two cars collide in a hit-and-stick collision. Determine their velocity immediately after the collision.
Let's begin by using the p=m•v equation to calculate the momentum of the two individual cars before the collision:
Jillian + Car: p = m•v = (185 kg)•(1.45 m/s) = 268.25 kg•m/s, South
Elissa + Car: p = m•v = (205 kg)•(1.75 m/s) = 358.75 kg•m/s, West
(Rounding will be done at the end of the problem.)
Now let's construct a vector addition diagram and calculate the total momentum of the system before the collision using the Pythagorean theorem.
The total momentum of the system before the collision is equal to the total momentum of the system after the collision. The ptotal is 447.95 kg•m/s. The total mass (mtotal) of these two players is 185 kg + 205 kg or 390 kg. Now we can use the total momentum and the total mass to calculate the after-collision velocity value of each of the objects.
v = ptotal / mtotal = (447.95 kg•m/s) / (390 kg) = 1.14859 ...m/s
v = 1.15 m/s
Check Your Understanding
Question 1:
A red bumper car (m = 250 kg) moving east at 1.05 m/s collides with a blue bumper car (m = 215 kg) moving south at 1.12 m/s. The collision is a hit-and-stick collision. Determine the magnitude and direction of the post-collision velocity immediately after the collision.
 Question 2:
Question 2:
Consider our familiar situation:
Ima Rilla Saari is driving her 1000-kg car northward across lanes of the parking lot with a speed of 2.0 m/s. Ben Abaday is driving his 1000-kg car westward with a speed of 1.5 m/s. The two cars collide, entangle, and travel together across the ice at a speed of 1.25 m/s in a direction that is 53.1° N of W.
Suppose that Ima's car had twice the mass (2000 kg) but the same speed of 2.0 m/s. What affect would this have upon the post-collision direction of the two cars? Support your claim with some reasoning.
Question 3:
Referring to the situation above. Suppose that both Ima's car and Ben's car had twice the mass (2000 kg). What affect would this have upon the post-collision direction of the two cars? Support your claim with some reasoning.
Question 4:
Referring to the situation above. Suppose that Ben's car had twice the speed (3.0 m/s). What affect would this have upon the post-collision direction of the two cars? Support your claim with some reasoning.
Question 5:
Referring to the situation above. Suppose that Ben's car had twice the speed (3.0 m/s) and one-half the mass (500 kg). What affect would this have upon the post-collision speed and direction of the two cars? Support your claim with some reasoning.