Forces in Two Dimensions - Complete Toolkit
Objectives
-
To use vector concepts to add force vectors and determine the resultant or net force.
-
To use vector concepts to determine the components of a force that is directed at an angle.
-
To use Newton’s laws and vector concepts to analyze objects that are at equilibrium (e.g., an object hung by two cables stretched diagonally to support points).
-
To use vector resolution and Newton’s second law to determine the acceleration of an object along a level surface when a force is applied to it at an angle to the surface.
-
To use free-body diagrams and Newton’s second law to analyze the motion of an object moving along an inclined plane.
-
To conduct a Newton’s second law analysis of a two-body system that includes two objects connected by a rope that is stretched over a pulley (e.g., an Atwood’s or modified Atwood’s machine).
Readings from The Physics Classroom Tutorial
-
The Physics Classroom Tutorial, Motion and Forces in Two-Dim. Chapter, Lesson 3
http://www.physicsclassroom.com/class/vectors
Interactive Simulations
-
Vector Addition
 The Vector Addition Interactive provides learners with a tool for visualizing the addition of vectors using either the head-to-tail method or the component method. Up to three vectors can be added and the resultant is drawn. The components of each vector can be toggled on and off; the magnitudes of the components are displayed as a numerical value. The Interactive can serve as a great tool for learning how vectors add together. This HTML5 interactive works on all devices.
The Vector Addition Interactive provides learners with a tool for visualizing the addition of vectors using either the head-to-tail method or the component method. Up to three vectors can be added and the resultant is drawn. The components of each vector can be toggled on and off; the magnitudes of the components are displayed as a numerical value. The Interactive can serve as a great tool for learning how vectors add together. This HTML5 interactive works on all devices.
-
Name That Vector
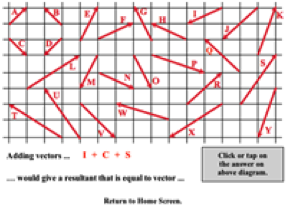 This skill-building activity presents 12 randomly-selected challenges to students. Each challenge involves the task of using components to add vectors. Vectors are presented graphically on a background grid so that the horizontal and vertical components can be easily determined. The Interactive reinforces the concept that the components of the resultant vector is the sum of the components of the individual vectors. This HTML5 Interactive works on tablets and Chromebooks; perfect for the 1:1 classroom.
This skill-building activity presents 12 randomly-selected challenges to students. Each challenge involves the task of using components to add vectors. Vectors are presented graphically on a background grid so that the horizontal and vertical components can be easily determined. The Interactive reinforces the concept that the components of the resultant vector is the sum of the components of the individual vectors. This HTML5 Interactive works on tablets and Chromebooks; perfect for the 1:1 classroom.
-
Sliding Down an Incline Plane
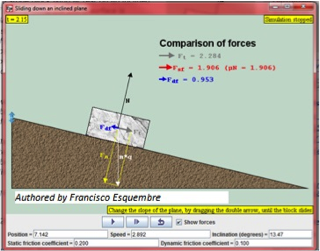 This Java simulation shows a stone block lying at rest on an inclined plane. Initially, the component of gravity along the plane surface is exceeded by the force of static friction. The slope of the ramp can be increased or decreased, allowing students to see the exact point when the component of gravity equals the force of static friction. If the ramp is raised any further, the block will slide down. The coefficient of static friction is set at 0.2. As the slope is increased or decreased, students will see changing numerical values for the gravitational component, the force of static friction, and the force of kinetic friction.
This Java simulation shows a stone block lying at rest on an inclined plane. Initially, the component of gravity along the plane surface is exceeded by the force of static friction. The slope of the ramp can be increased or decreased, allowing students to see the exact point when the component of gravity equals the force of static friction. If the ramp is raised any further, the block will slide down. The coefficient of static friction is set at 0.2. As the slope is increased or decreased, students will see changing numerical values for the gravitational component, the force of static friction, and the force of kinetic friction.
-
PhET: The Ramp
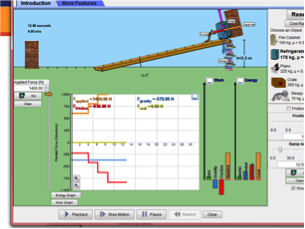 For teachers who want to take a deeper dive into mechanical advantage and real-life connections, "The Ramp" simulation is a good start. You can push a variety of objects up a virtual ramp: a file cabinet, refrigerator, piano, crate, or a sleepy dog! Set the coefficient of friction, set the ramp angle from 1-90 degrees, and change the applied force from 0-3000 Newtons. This gives the simulation powerful flexibility. And if that's not enough ... students can view related free-body diagrams and graphs of energy and forces.
For teachers who want to take a deeper dive into mechanical advantage and real-life connections, "The Ramp" simulation is a good start. You can push a variety of objects up a virtual ramp: a file cabinet, refrigerator, piano, crate, or a sleepy dog! Set the coefficient of friction, set the ramp angle from 1-90 degrees, and change the applied force from 0-3000 Newtons. This gives the simulation powerful flexibility. And if that's not enough ... students can view related free-body diagrams and graphs of energy and forces.
For a turn-key activity to accompany this simulation, try The Ramp Student Guide Developed by a high school teacher, this lesson is simple enough to be completed without extensive prior knowledge. It will keep beginners on task as they tackle the multiple elements of this simulation. It asks probing questions about the nature of the forces at play when objects move on an incline plane.
For a more in-depth lesson that introduces calculation of the ideal and actual mechanical advantage of the inclined plane, click here: "The Ramp" - Mechanical Advantage Allow 60-90 minutes
Video and Animations
-
Physlet Physics: Two-Dimensional Kinematics
 This Physlets chapter provides a comprehensive collection of 17 animation-based problems consisting of: 1) Illustrations, 2) Explorations (accompanied by printable worksheets), and 3) Multi-step problems. The resources vary from multiple choice format to longer exercises that require students to integrate multiple representations and solve problems. Topics include projectile motion, motion on an incline, circular motion, constant acceleration, objects in flight, and more. Free access with attribution.
This Physlets chapter provides a comprehensive collection of 17 animation-based problems consisting of: 1) Illustrations, 2) Explorations (accompanied by printable worksheets), and 3) Multi-step problems. The resources vary from multiple choice format to longer exercises that require students to integrate multiple representations and solve problems. Topics include projectile motion, motion on an incline, circular motion, constant acceleration, objects in flight, and more. Free access with attribution.
-
PBS Learning Media: Segway Technology – What’s Newton Got to Do With It?
 Did you know.....the Segway is described by its inventor, Dean Kamen, as an inverted pendulum system. The person driving is like the pendulum mass, oscillating back and forth over the transporter. In this 8-minute video, Kamen talks about how Newton's Laws governed the Segway design, which uses gyroscopic sensors to detect changes in the driver's center of mass. The electric engine provides the power and is remarkably economical to operate. This video could be a very engaging way to spark discussions about applied force.
Did you know.....the Segway is described by its inventor, Dean Kamen, as an inverted pendulum system. The person driving is like the pendulum mass, oscillating back and forth over the transporter. In this 8-minute video, Kamen talks about how Newton's Laws governed the Segway design, which uses gyroscopic sensors to detect changes in the driver's center of mass. The electric engine provides the power and is remarkably economical to operate. This video could be a very engaging way to spark discussions about applied force.
Interactive Homework Problems
If you haven’t encountered physicist Gary Gladding’s research-based homework problems, you’re in for a great surprise! The digital problems present physical situations that are commonly experienced in life. Each problem has 3 components: conceptual analysis, strategic analysis, and calculation. As students go through the sequence, they answer multiple choice questions designed to encourage critical thinking. Immediate feedback is provided at each step. Liberal use of free-body diagrams, drawings, and graphs help the learner visualize the concepts being introduced. Even students who struggle with the content will feel comfortable with the pacing. Can be performed independently or used as a flipped lesson.
-
Illinois PER Interactive Problem: Stream Crossing
 This problem presents the 2-dimensional motion situation of swimming directly across a stream that has a current speed of 10 feet/minute. It requires some thought to realize that the current is countering the motion to swim in a straight line. Once this is recognized, the author takes learners through each step of finding the x components of the two vector velocities to solve the problem.
This problem presents the 2-dimensional motion situation of swimming directly across a stream that has a current speed of 10 feet/minute. It requires some thought to realize that the current is countering the motion to swim in a straight line. Once this is recognized, the author takes learners through each step of finding the x components of the two vector velocities to solve the problem.
-
Illinois PER Interactive Problem: Mass on Two Strings
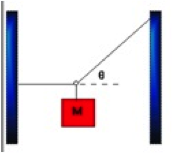 A block of known mass is suspended from two strings attached to walls. One string is horizontal; the other is at a 50-degree angle to horizontal. Students will use free-body diagrams and Newton's Laws to figure out the tension on the left string.
A block of known mass is suspended from two strings attached to walls. One string is horizontal; the other is at a 50-degree angle to horizontal. Students will use free-body diagrams and Newton's Laws to figure out the tension on the left string.
-
Illinois PER Interactive Problem: Plane in Flight
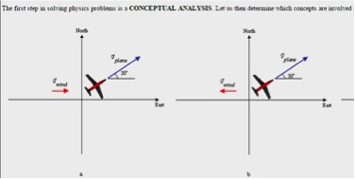 This problem presents students with an airplane just after liftoff which is traveling at a known airspeed and with a headwind of known velocity. The flight trajectory is also given. The problem: students must figure out the speed of the plane relative to the ground. The problem is not as easy as it first appears....both the airplane velocity and the wind velocity have x and y components. The math isn't especially difficult, but the strategy requires thought. The problem should give beginners a solid way to understand the scope of kinematics in two dimensions.
This problem presents students with an airplane just after liftoff which is traveling at a known airspeed and with a headwind of known velocity. The flight trajectory is also given. The problem: students must figure out the speed of the plane relative to the ground. The problem is not as easy as it first appears....both the airplane velocity and the wind velocity have x and y components. The math isn't especially difficult, but the strategy requires thought. The problem should give beginners a solid way to understand the scope of kinematics in two dimensions.
-
Illinois PER Interactive Problem: Block on Incline
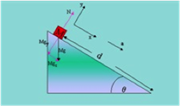 In this problem, students relate Newton’s Second Law and gravitational acceleration as a block slides down an incline. At first the block is at rest atop the incline. Given the angle of incline and the ramp length, learners must determine the time required for the block to reach the bottom under the force of gravity alone. (Great problem for students who are struggling conceptually with this unit of study.)
In this problem, students relate Newton’s Second Law and gravitational acceleration as a block slides down an incline. At first the block is at rest atop the incline. Given the angle of incline and the ramp length, learners must determine the time required for the block to reach the bottom under the force of gravity alone. (Great problem for students who are struggling conceptually with this unit of study.)
Labs and Investigations
-
The Physics Classroom, The Laboratory, Getting Hung Up by Tension
Students conduct force analysis on three different objects held at static equilibrium. Vector resolution is used for each individual force to determine their components. Components are added to determine the resultant force.
-
The Physics Classroom, The Laboratory, Sign Hanging Lab
Students measure the tension force exerted upon a hanging sign in order to predict the mass of the sign.
-
The Physics Classroom, The Laboratory, Science Friction Adventure
Students measure the value of the friction coefficient for an inclined plane and compare it to the value for the maximum angle at which the plane can be inclined before an object overcomes the static friction force and slides down it.
-
The Physics Classroom, The Laboratory, Inclined Plane Lab
Students work as a class, with each lab group taking a different angle, in order to determine the ratio of the applied force required to hold a cart at rest to the weight. The ratios and angle values are used to discover the relationship between weight, angle and the parallel component of gravity.
-
The Physics Classroom, The Laboratory, On a Roll Challenge
Students combine Newton's laws and kinematics to predict the speed of a cart at the end of an inclined plane and compare the predicted value to the actual value.
-
The Physics Classroom, The Laboratory, Modified Atwood’s Machine
Students explore the relationship between final velocity and the amount of hanging mass on a modified Atwood's machine.
Minds On Physics Internet Modules:
The Minds On Physics Internet Modules are a collection of interactive questioning modules that target a student’s conceptual understanding. Each question is accompanied by detailed help that addresses the various components of the question.
-
Forces in Two Dimensions module, Ass’t 2D1 - Vector Analysis
-
Forces in Two Dimensions module, Ass’t 2D2 - Fnet = m•a and Forces at Angles
-
Forces in Two Dimensions module, Ass’t 2D3 - Equilibrium Concepts
-
Forces in Two Dimensions module, Ass’t 2D5 - Static Equilibrium and Analysis
-
Forces in Two Dimensions module, Ass’t 2D5 - Inclined Plane Concepts
-
Forces in Two Dimensions module, Ass’t 2D6 - Incline Plane Analysis
Concept Building Exercises:
-
The Curriculum Corner, Forces in Two Dimensions, Another Angle on F-m-a
-
The Curriculum Corner, Forces in Two Dimensions, Adding and Resolving Forces
-
The Curriculum Corner, Forces in Two Dimensions, Analyzing Equilibrium Situations
-
The Curriculum Corner, Forces in Two Dimensions, Analyzing Accelerations on Level Surfaces
-
The Curriculum Corner, Forces in Two Dimensions, Inclined Plane Analysis
Problem-Solving Exercises:
-
The Calculator Pad, Vectors and Forces in Two Dimensions, Problems #1 - #27
Real Life Connections:
-
CIESE – Navigational Vectors
 This high school instructional unit features nine lessons relating to vectors. Students build understanding of vector properties as they learn airplane navigation. Project-based activities include reading real-time weather maps, tracking airplanes flying in U.S. skies, calculating vector components, analyzing effects of wind velocity, and completing training similar to a private pilot certification program. The unit culminates with an online pilot flight test. Comprehensive teacher guides, student guides , reference materials, and assessments are included.
This high school instructional unit features nine lessons relating to vectors. Students build understanding of vector properties as they learn airplane navigation. Project-based activities include reading real-time weather maps, tracking airplanes flying in U.S. skies, calculating vector components, analyzing effects of wind velocity, and completing training similar to a private pilot certification program. The unit culminates with an online pilot flight test. Comprehensive teacher guides, student guides , reference materials, and assessments are included.
Elsewhere on the Web:
-
Tilt Maze Game Model Java-Based game
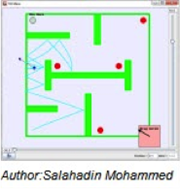 The Tilt Maze Game Model is a recent addition to Open Source Physics. The model is set on a plane that can be tilted to make the ball roll due to gravity. The plane can be tilted up, down, to the left and to the right. By tilting the planes, the user must cause the ball to move through the maze to get to the hole at the top left side of the maze...but be careful, there are some traps laid out that would stop you from accomplishing your goal.
The Tilt Maze Game Model is a recent addition to Open Source Physics. The model is set on a plane that can be tilted to make the ball roll due to gravity. The plane can be tilted up, down, to the left and to the right. By tilting the planes, the user must cause the ball to move through the maze to get to the hole at the top left side of the maze...but be careful, there are some traps laid out that would stop you from accomplishing your goal.
Standards:
A. Next Generation Science Standards (NGSS)
Disciplinary Core Ideas
-
HS-PS2.1.i Newton’s second law accurately predicts changes in the motion of macroscopic objects
Crosscutting Concepts
Scale, Proportion, and Quantity
-
Algebraic thinking is used to examine scientific data and predict the effect of a change in one variable on another
Systems and System Models
-
When investigating or describing a system, the boundaries and initial conditions of the system need to be defined.
Science and Engineering Practices
Practice #1: Analyzing and Interpreting Data
-
Analyze data using computational models in order to make valid and reliable scientific claims.
Practice #2: Developing and Using Models
-
Develop and use a model based on evidence to illustrate the relationships between systems or between components of a system.
-
Use a model to provide mechanistic accounts of phenomena.
Practice #3: Planning and Carrying Out Investigations
-
Plan and conduct an investigation individually and collaboratively to produce data to serve as the basis for evidence … and consider limitations on the precision of the data
-
Select appropriate tools to collect, record, analyze, and evaluate data.
-
Collect data about a complex model or system to identify failure points or improve performance relative to criteria for success or other variables.
Practice #6: Constructing Explanations
-
Construct and revise an explanation based on valid and reliable evidence obtained from a variety of sources (including students’ own investigations, models, theories, simulations) and the assumption that theories and laws that describe the natural world operate today as they did in the past and will continue to do so in the future.
Practice #8: Obtaining, Evaluating, and Communicating Information: High School
-
Use mathematical representations of phenomena to support claims.
-
Use mathematical representations of phenomena to describe explanations.
Create or revise a computational model or simulation of a phenomenon, designed device, process, or system.
B. Common Core Standards for Mathematics – Grades 9-12
Standards for Mathematical Practice:
-
Reason abstractly and quantitatively
-
Model with mathematics
-
Look for and express regularity in repeated reasoning
Number and Quantity – Vector and Matrix Quantities
-
N-VM.1 Recognize vector quantities as having both magnitude and direction. Represent vector quantities by directed line segments and use appropriate symbols for vectors and their magnitudes.
-
N-VM.2 Find the components of a vector.
-
N-VM.4.a Add vectors end-to-end, component-wise, and by the parallelogram rule. Understand that the magnitude of a sum of two vectors is typically not the sum of its magnitudes.
-
N-VM.4.b Given two vectors in magnitude and direction form, determine the magnitude and direction of their sum.
-
N-VM.4.c Understand vector subtraction v – w as v + (-w) where –w is the additive inverse of w, with the same magnitude as w and pointing in the opposite direction. Represent vector subtraction graphically by connecting the tips in the appropriate order, and perform vector subtraction component-wise.
Algebra – Reasoning with Equations and Inequalities
-
A-REI.4.b Solve quadratic equations by inspection (e.g., for x squared = 49), taking square roots, completing the square, the quadratic formula, and factoring, as appropriate to the initial form of the equation.
-
A-REI.10 Understand that the graph of an equation in two variables is the set of all its solutions plotted in the coordinate plane, often forming a curve.
Functions – Interpreting Functions
-
F-IF.4 For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship.
-
F-IF.6 Calculate and interpret the average rate of change of a function (presented symbolically or as a table) over a specified interval. Estimate the rate of change from a graph.
Functions – Trigonometric Functions
-
Use special triangles to determine geometrically the values of sine, cosine, tangent.
C. Common Core Standards for English/Language Arts (ELA) – Grades 9-12
Reading Standards for Literacy in Science and Technical Subjects
Key Ideas and Details: High School
-
RST.9-10.2 Determine the central ideas or conclusions of a text; trace the text’s explanation or depiction of a complex process, phenomenon, or concept; provide an accurate summary of the text.
-
RST.9-10.3 Follow precisely a complex multistep procedure when carrying out experiments, taking measurements, or performing technical tasks, attending to special cases or exceptions defined in the text.
Craft and Structure – High School
-
RST.11-12.4 Determine the meaning of symbols, key terms, and other domain-specific words and phrases as they are used in a specific scientific or technical context relevant to grades 11-12 texts and topics.
Integration of Knowledge and Ideas – High School
-
RST.11-12.7 Integrate and evaluate multiple sources of information presented in diverse formats and media in order to address a question or solve a problem.
-
RST.11-12.8 Evaluate the hypotheses, data, analysis, and conclusions in a science or technical text, verifying the data when possible and corroborating or challenging conclusions with other sources of information.
-
RST.11-12.9 Synthesize information from a range of sources (e.g., texts, experiments, simulations) into a coherent understanding of a process, phenomenon, or concept, resolving conflicting information when possible.)
Range of Reading and Level of Text Complexity – High School
-
RST-9-10.10 By the end of Grade 10, read and comprehend science/technical texts in the grades 9-10 text complexity band independently and proficiently.
D. College Ready Physics Standards (Heller and Stewart)
Grades 9-12 : Newton’s Laws
Objective 3.2: Forces and Changes in Motion – Essential Knowledge
H.3.2.2 Newton’s second law of motion includes the following ideas:
-
The linear acceleration of an object is directly proportional to the vector sum of all the forces acting on the object and inversely proportional to the object’s mass (a = "F/m). The vector sum of all the forces (net force) is not a real force caused by an interaction with another object. The single force that could replace the original multiple forces and cause the same acceleration of the object is the vector sum of forces.
-
A special case of Newton’s second law occurs when the vector sum of all the forces (net force) on an object is zero. In this case, there is no acceleration and the object remains at rest or maintains a constant speed and a constant direction of motion.
Objective 3.2: Forces and Changes in Motion – Learning Outcomes
-
Analyze force diagrams to determine if they accurately represent different situations involving multiple contact, gravitational and/or electrical interactions. Interpret the meaning of the vector sum of all the forces (net force).
-
Analyze different problems involving at least two different types of interactions (contact, gravitational, magnetic and/or electrical) and an identified object of interest.
-
Represent the forces acting on the object of interest by drawing a force diagram showing both the vertical and horizontal forces. When appropriate, use vector addition to determine the relative size and direction of the sum of all the forces (net force), and interpret the meaning of the net force.
-
Explain the observed motion of the object of interest. Justification is based on Newton’s second law.
Objective 3.3: Contact Interactions and Forces – Essential Knowledge
H.3.3.1 The types of interactions of the object/system of interest with its surroundings and the force laws for each type of interaction must be identified in order to use Newton’s laws to quantitatively explain and predict the motion of an object or system.
H.3.3.2 There are empirical force laws for some types of contact interactions.
-
The force of kinetic friction always acts in the opposite direction of the relative velocity of the object with respect to the surface it is sliding over. The magnitude of the kinetic friction depends on the types of materials that make up the two surfaces sliding past each other and the magnitude of the compression force acting on the object. This can be mathematically represented by Fk = μkN.
H.3.3.3 There are no force laws for some types of contact interactions because the complexity of the interactions does not allow the magnitude of the forces to be easily represented.
-
A contact interaction occurs when the surfaces of two solid objects are pressed together because of other interactions on one or both objects (e.g., a solid sitting on or sliding along a table; a magnet attached to a refrigerator). This is called a compression interaction. A compression (normal) force applied to an object is always a push directed at right angles from the surface of the other interacting object.
-
A contact interaction occurs when a cord (e.g., rope, wire, rod) pulls on another object or system and the cord is not slack. A tension force on an object always points in the direction the cord is pulling.
H.3.3.5 During contact interactions, forces are not transferred to objects (unlike energy) – the interaction stops as soon as the objects stop touching. Simplifying assumptions are often needed to gain a basic understanding of a real-world situation or to solve a problem (e.g., for contact interactions, “massless” ropes, “frictionless” sliding surfaces, maximum static friction and negligible air resistance).
Objective 3.4: Gravitational Interaction and Forces – Learning Outcomes
-
Explain why all objects near Earth’s surface fall with approximately the same acceleration, despite having different masses and weights. Justify by using the universal law of gravitation and Newton’s second law.
-
Analyze different problems to determine whether a constant gravitational acceleration can be assumed. Justify the analysis by using the universal law of gravitation. When appropriate, calculate a gravitational force.