 Collisions
Collisions
Resource:
Science Reasoning Center: Collisions
Grade Level: High School
Description:
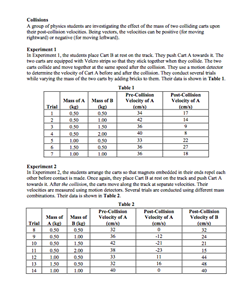
This passage describes two experiments in which the inelastic and elastic collisions of two carts on a track are investigated. Mass, pre-collision velocities, and post-collision velocities of the carts are described using two data tables. Questions target a student's ability to understand the experimental design, to identify the effect of one variable on another, to draw conclusions consistent with the data, and to interpolate and extrapolate from the given data in order to predict the result of additional trials.
Performance Expectation:
HS-PS2-2 Use mathematical representations to support the claim that the total momentum of a system of objects is conserved when there is no net force on the system.
This activity aligns with the three dimensions of the Next Generation Science Standards in the manner described below:
| Force and Motion (HS-PS2.A.3): If a system interacts with objects outside itself, the total momentum of the system can change; however, any such change is balanced by changes in the momentum of objects outside the system. |
This passage focuses on data analysis for a ‘hit and stick’ collision and a ‘hit and bounce off’ collision. The student may choose to consider the system as both carts—in which case the momentum of the system remains unchanged in the collision. If the reader defines the system as only one cart, then the system’s momentum does change but it is balanced by changes in the momentum of the other cart that is outside the system. |
| Cause and Effect: Cause and effect relationships can be suggested and predicted for natural and designed systems by examining what is known about smaller-scale mechanisms within the system. |
After considering two data presentations, the reader is asked to determine how changing one aspect of the experiment would affect present results. Questions 3 at the end of the passage, for example, require the student to reason through the effect of increasing the mass of a cart on post-collision velocities. |
| System and System Models: When investigating or describing a system, the boundaries and initial conditions of the system need to be defined. |
The experiments and data presentations in this passage require the student to analyze the changes in the carts’ post-collision motions by defining the system as either one or both carts involved in the collision. Analysis of collision experiments such as this can yield predictable post-collision velocities when the student evaluates the experiment by defining a system. |
| Planning and Carrying Out Investigations: Plan an investigation individually and collaboratively to produce data to serve as the basis for evidence in building/revising models, supporting explanations for phenomena, or testing solutions to problems. |
Questions 1 and 2 in this passage address the student’s ability to both understand and critique the experimental design. Students must identify the dependent variable in the experiment and identify a legitimate criticism inherent to the experiment's design. |
| Analyzing and Interpreting Data: Analyze data using computational models in order to make valid and reliable scientific claims. |
With cart masses, pre-collision cart velocities, and post-collision velocities presented in two large data sets, the learner must navigate a considerable amount of information from two separate experiments. Questions 5, 6, 10, and 12 require students to both analyze individual data presentations as well as combine data from both data representations simultaneously. |
| Constructing Explanations and Designing Solutions: Apply scientific principles and evidence to provide an explanation of phenomena and solve design problems, taking into account possible unanticipated effects. |
Reasoning from his or her understanding of the physics principle that governs a collision experiment, the student is called upon to construct an explanation as to why the cart collision data looks the way it does. Questions 3, 9, and 13 from this passage require students to both construct explanations as well as predict conditions that would allow one cart in the collision to have the largest post-collision velocity. |
| Using Mathematical and Computational Thinking: Use mathematical and/or computational representations of phenomena or design solutions to support explanations. |
As conservation of momentum is a powerful tool in allowing a scientist to use a mathematical model to predict velocities after a collision, Questions 4, 7, 8, and 11 from this passage address the reader’s ability to use mathematical and computational thinking to make such predictions. |
Associated Reading from The Physics Classroom
Other Supporting Pages at The Physics Classroom:
- The Curriculum Corner: Collision Analysis; Momentum Conservation as a Guide to Thinking; Momentum Problem-Solving
View Infographic.
(Coming Soon)
Search the NGSS Corner
Maybe you're looking for something really specific that pertains to a desired topic and emphasizes one or more of the listed NGSS dimensions. Why not try a search of this section of our website? Simply select from one or more of the pull-down menus and click Search This page will reload and a collection of possibilities will be displayed in this section of the page and sorted by relevancy.