Lesson 2: Quantitative Analysis of Compounds

Part d: Empirical and Molecular Formulae

Part a: Molar Mass of Compounds
Part b: Grams-Moles-Particles Relationship
Part c: Percent Composition
Part d: Empirical and Molecular Formulae

 

What’s in a Formula?

On the previous page, the importance of the question…

… was discussed. A molecular formula and the composition of a compound are closely related. A molecular formula indicates which elements are present in a compound and the number of atoms of each element in a molecule of the compound. Every molecule of H₂O has two atoms of hydrogen and one atom of oxygen. On this page, we will learn how a molecular formula is determined from experimental data.
 
 
 

 

The Simplest Formula

Laboratory chemists are capable of analyzing a compound and determining the mass of each element present in the compound. Typical data from such analyses look like this:

 
This mass information can be used to determine the moles of the two elements – H and O – in the 10.000-gram sample. By dividing by the molar mass, we can determine …
  The analysis determines that the sample contains equal moles of H and O. Put another way, there are an equal number of atoms of H and O in a molecule of this compound. If you have a collection of equal numbers of H and O atoms, then there are multiple ways to assemble them into molecules. As such, the molecular formula could be HO or H₂O₂ or H₃O₃ or H₄O₄, etc. From this data alone, there is no way of knowing the molecular formula. All that is known is that the subscripts on the two elements must be identical.
 

 

 
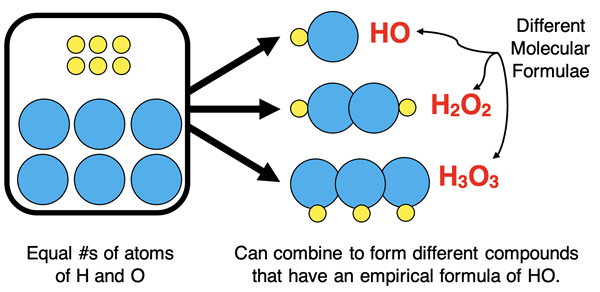
Chemists settle on what is referred to as the simplest formula. The simplest formula indicates the simplest ratio of atoms of the elements. For the above compound, the simplest formula is HO (subscripts of 1 are not included). Another name for simplest formula is empirical formula. It is referred to as an empirical formula because it is determined empirically (by experimental analysis).
 

 

 

 

Empirical Formula vs. Molecular Formula

The empirical or simplest formula is not necessarily the molecular formula and is sometimes quite different than the molecular formula. While the empirical formula shows the simplest ratio of atoms, the molecular formula shows that actual ratio of atoms in a molecule of the compound. The subscripts on the molecular formula are always a whole number (1, 2, 3, 4, etc.) multiple of the subscripts on the empirical formula. The table below shows the molecular formula and empirical formula for several compounds.

 
 
 

Analysis of Mass Composition Data

There are a variety of experimental methods used to determine the mass composition for the elements in an unknown compound. Our goal is to learn how to use such data and determine the empirical formula. The method is quite straightforward and based primarily on the skill of converting from mass to moles. After several examples, we will learn how to determine a molecular formula from the empirical formula and molar mass data.
 

 

Method for Determining an Empirical Formula from Mass Data

Experimental analysis of an unknown compound will most commonly yield data in one of two formats. One format includes the mass in grams of each element in the compound. The method for determining the empirical formula from mass data is:
 

1. For each element, use molar mass values and conversion factors to determine the # of moles of each element.
2. Determine the simplest ratio of moles for all the elements. This is typically done by dividing the larger number of moles by the smaller number of moles.
3. Analyze the results to determine the simplest set of whole number subscripts.

 
The process that takes place after step 2 can be quite varied. It takes much thoughtful practice to acquire the skill of determining the whole number subscripts from the step 2 results. Let’s talk through some examples that assume three elements (X, Y, and Z) in a compound with an empirical formula of the format X_aY_bZ_c where a, b, and c are the simplest whole number subscripts.
 
For Compound X_aY_bZ_c, step 2 results:  
The resulting numbers are close enough to whole numbers to round to 1, 2, and 1. This yields the empirical formula of X₁Y₂Z₁ or more appropriately XY₂Z.
 
As a second example, suppose step 2 provides the ratios …
 
For Compound X_aY_bZ_c:  
The X ratio is nowhere close to a whole number. The most reasonable approach at this point is to multiply each ratio by two. This yields new ratios of 2.98, 2.00, and 2.04. These ratios are close enough to whole numbers to conclude on an empirical formula of X₃Y₂Z₂.
 
As a final example, suppose step 2 provides the ratios …
 
For Compound X_aY_bZ_c:  
Once again there are one or more ratios (the X and the Y ratios) that are nowhere close to a whole number. The most reasonable approach at this point is to multiply each ratio by three. This yields new ratios of 3.96, 4.02, and 3.00. These ratios are close enough to whole numbers to conclude on an empirical formula of X₄Y₄Z₃.
 
Always keep in mind that you are analyzing experimental data and it is sometimes messy, and at other times, real messy. Don’t expect the analysis to yield perfect whole numbers. Errors in the experimental process are going to result in ratios like 3.96, 4.02, and 3.00 instead of the more perfect 4.00, 4.00, and 3.00. With relatively accurate data, you should be able to comfortably arrive at a set of whole number subscripts using simple multipliers of 2, 3, 4, and 5. Avoid taking ratios like 1.24, 1.01, and 1.00 and using large multipliers like 100 to end up with an empirical formula of X₁₂₄Y₁₀₁Z₁₀₀.
 
Examples 1 and 2 illustrate the use of these strategies.
 
     

Example 1

 
 
Solution:
 
Step 1: Determine moles of each element Step 2: Determine the simplest ratio of the two elements  
Step 3: Determine whole number subscripts for each element
   
 
 

Example 2

 
 
Solution:
 
Step 1: Determine moles of each element
   
Step 2: Determine the simplest ratio of the three elements
   
Step 3: Determine whole number subscripts for each element
       

Method for Determining an Empirical Formula from Percent Composition Data

Experimental analysis of an unknown compound can also yield data as percent composition (by mass) for each element in the compound. The method for determining the empirical formula from percent composition data is:
 

1. Assume a 100.00-gram sample. Use the percent composition data to determine the mass of each element in a 100.00-gram sample.
2. For each element, use molar mass values in conversion factors to determine the # of moles of each element in the 100.00-gram sample.
3. Determine the simplest ratio of moles for all the elements. This is typically done by dividing the larger number of moles by the smaller number of moles.
4. Analyze the results to determine the simplest set of whole number subscripts. This final analysis will proceed in an identical manner as described above.

 
Examples 3 and 4 illustrate the use of this method.
 
 
 

Example 3

 
 
Solution:
 
Step 1: Determine mass of each element in a 100.00-gram sample
   
Step 2: Determine moles of each element
   
Step 3: Determine the simplest ratio of the two elements
   
Step 4: Determine whole number subscripts for each element
   
 
 
 

Example 4

 

Solution:
 
Step 1: Determine mass of each element in a 100.00-gram sample
   
Step 2: Determine moles of each element
   
Step 3: Determine the simplest ratio of the three elements
   
Step 4: Determine whole number subscripts for each element
   
 
 
 

Determining a Molecular Formula

A molecular formula cannot be determined solely from mass composition data. A molar mass value is required to determine the molecular formula from an empirical formula. The subscripts of a molecular formula are a whole number multiple (1, 2, 3, 4, etc.) of the subscripts in the empirical formula. For this reason, the molar mass of the actual compound is also the same whole number multiple of the mass per mole of the empirical formula.
 
Suppose that you determine an unknown compound has an empirical formula of CH₂O. And suppose that you determine that the molar mass is 60.0 g/mol. The mass per mole of CH₂O is …
   
The molar mass (given as 60.0 g/mol) is two times the mass per mole of CH₂O. Therefore, the subscripts in the molecular formula must be two times those of CH₂O. The molecular formula is C₂H₄O₂.
 
The table below demonstrates the relationship between the empirical formula, the molar mass, and the molecular formula. If you know the empirical formula and the molar mass, then you can determine the subscript multiplier and determine the molecular formula.
   
 
 
 

Before You Leave

• Download our Study Card on Empirical vs. Molecular Formulae. Save it to a safe location and use it as a review tool.
• Our Calculator Pad section has two sets of Practice Problems on this topic. Your answers are evaluated and feedback is provided; you have infinite opportunities to correct your mistakes. Try …
  • Problem Set PMG13 – Determining Formula from Percent Composition 1.
  • Problem Set PMG14 – Determining Formula from Percent Composition 2.
• The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.

 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. A chemical formula of a compound represents ______.

1. the relative mass of each element in the compound
2. the relative number of each type of atom in the compound
3. the relative atomic masses of each element in the compound

 

 

2. A distinction is made between the simplest formula and the molecular formula.  The simplest formula is sometimes referred to as the empirical formula.  What is the empirical formula of a compound which has the molecular formula of …

1. … P₄O₁₀? 
   
   Check Answer
   Answer: P₂O₅
   
   The subscripts 4 and 10 in the molecular formula can be reduced by a factor of 2.
   
    
   
    
2. … C₈H₁₈? 
   
   Check Answer
   Answer: C₄H₉
   
   The subscripts 8 and 18 in the molecular formula can be reduced by a factor of 2.
   
    
   
    
3. … H₂SO₄? 
   
   Check Answer
   Answer: H₂SO₄
   
   The subscripts already express the lowest, simplest ratio of atoms.
   
    
   
    

 
​ 
 
3. Formulas of compounds indicate atom ratios of the elements in the compound. 

1. So, the formula CO₂ indicates that there is/are _____ atom(s) of C and _____ atom(s) of O in 1 molecule of CO₂. 
   
   Check Answer
   Answer:
   So, the formula CO₂ indicates that there is/are 1 atom(s) of C and 2 atom(s) of O in 1 molecule of CO₂.
   
    
   
    
2. Similarly, the formula Ca₃(PO₄)₂ indicates that there is/are _____ atom(s) of Ca,  _____ atom(s) of P, and _____ atom(s) of O in 1 molecule of Ca₃(PO₄)₂. 
   
   Check Answer
   Answer: 
   Similarly, the formula Ca₃(PO₄)₂ indicates that there is/are 3 atom(s) of Ca,  2 atom(s) of P, and 8 atom(s) of O in 1 molecule of Ca₃(PO₄)₂. 
   
    
   
    

 

 
4. Determine the empirical formula for a compound having the following ratio of C, N, H, and O atoms?

• 1.20 x 10²¹ N atoms
• 2.40 x 10²¹ O atoms
• 6.00 x 10²¹ C atoms
• 12.00 x 10²¹ H atoms

 

1. C₅H₁₀O₂N
2. C₆H₁₂O₂N
3. C₆H₁₂O₃N
4. C₆H₁₂O₂₄N

 
 

 
​
 
5. The subscripts in the molecular formula _____ the subscripts in the empirical formula.
are always the same as

1. are always a whole number multiple of
2. are often unrelated to
3. can seldom be found from

​ 

 

 
6. A compound is analyzed and found to contain the following percentages by mass:  45.56% tin (Sn) and 54.43% chlorine (Cl). Determine the empirical formula of this compound.
 
​ 

 

 
7. A highly odiferous organic compound has the empirical formula CH₂ and a molar mass of 70 g/mol. Determine the molecular formula of the compound.
 
​