Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 4: Calculations in Chemistry
Part b: Unit Conversions
Part 4a: The Factor Label Method
Part 4b: Unit Conversions
Part 4c: Significant Digits Revisited
The Metric System Revisited
 The Metric System was introduced in Lesson 2 of this Chapter. The metric system is a decimal-based system that relies on a set of base units (meter, gram, liter, second, etc.) for fundamental quantities like length, mass, volume, time, etc. Greek prefixes are used to modify these base units. Each Greek prefix has a particular numerical meaning. For instance, milli- means 1/1000-th, centi- means 1/100-th, and kilo- means 1000. A milliliter is equivalent to 1/1000-th of a liter. A centimeter is equivalent to 1/100-th of a meter. And a kilogram is equivalent to 1000 grams.
The Metric System was introduced in Lesson 2 of this Chapter. The metric system is a decimal-based system that relies on a set of base units (meter, gram, liter, second, etc.) for fundamental quantities like length, mass, volume, time, etc. Greek prefixes are used to modify these base units. Each Greek prefix has a particular numerical meaning. For instance, milli- means 1/1000-th, centi- means 1/100-th, and kilo- means 1000. A milliliter is equivalent to 1/1000-th of a liter. A centimeter is equivalent to 1/100-th of a meter. And a kilogram is equivalent to 1000 grams.
The Staircase Model of Unit Conversion
Because of the power-of-ten foundation of the metric system, conversion from one unit to another involves the movement of a decimal point a specified number of places. A common student struggle is determining which direction to move the decimal point and how many places to move it. All sorts of memorization schemes have been developed to assist students in this task. In Lesson 2, we presented the Staircase Model that relies upon the mnemonic King Henry Doesn’t Usually Drink Chocolate Milk. You can read more about the strategy here. While the strategy works well, it is limited to conversions between only seven units and it still involves some memorizing. Furthermore, its use is limited to metric conversion. It can’t be transferred to other types of conversions used in a typical Chemistry course. For these reasons, we believe that there is a much better approach – the factor label method.
Factor Label Method of Unit Conversion
The factor label method of unit conversion was introduced earlier in Lesson 4. The method uses converting factors to convert from a given quantity in one set of units to the same or a different quantity in a different set of units. For complex conversions, a collection of converting factors are strung together in consecutive fashion. The strategy involves creating conversion factors from equivalence statements such as 100 cm = 1 m and 1000 m = 1 km and then aligning units so that they cancel.

A detailed discussion was given earlier in Lesson 4. In this part of Lesson 4, we will learn how to use the factor label method to perform metric conversions. The method is still reliant on the meaning of the metric conversions. This information will either be provided or memorized. You should consult instructor for specifics regarding what Greek prefixes need to be memorized.
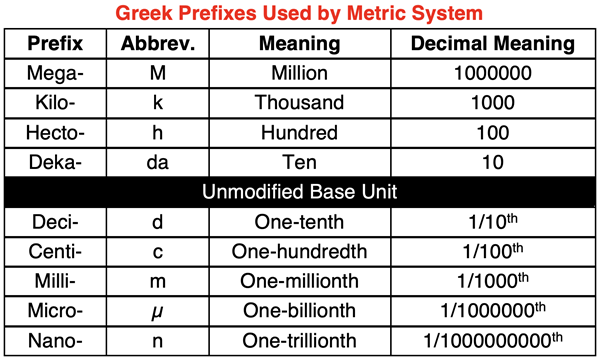
The factor label method of converting units is best learned by practice. Read about the method (here). Observe the examples of it in use (below). But more importantly, practice it yourself. There are some practice problems in the Check Your Understanding section and links to additional practice in the Before Your Leave section.
Example 1
Red light is measured to have a wavelength of 6.65x10-5 cm. Determine the wavelength in nanometers (nm). Given: 109 nm = 1 m; 100 cm = 1 m.
The solution begins by writing down the given quantity with its unit (6.65x10-5 cm) and setting up the conversion factors. The set-up of units comes first. Since the given quantity has units of cm, the unit cm will be placed in the denominator of the first conversion factor. The given information (100 cm = 1 m) indicates that cm are related to m. So, m is the unit in the numerator of the first conversion factor.
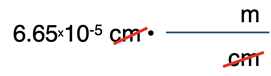
The unit cm will cancel and the unit m remains uncancelled. We want to determine the wavelength in nm. We need a second conversion factor to convert the m to nm. The unit m will be placed in the denominator of the second conversion factor. The given information indicates that m are related to nm. So, nm is the unit in the numerator of the second conversion factor.

Using the second conversion factor, the unit m will cancel and the unit nm remains uncancelled. That’s exactly the unit we wish to solve for. The units are set up perfectly.
Now we will give attention to numbers. As we do, we will inspect the two given equivalence statements - 109 nm = 1 m; 100 cm = 1 m - to determine where the numbers go. For the first conversion factor, we use 100 cm = 1 m as the guide to where to place the 1 and the 100. Since 100 is with cm in the equivalence statement, we put 100 with cm in the first conversion factor. This puts the 1 with m in the first conversion factor. The process is repeated for the second conversion factor using 109 nm = 1 m. Since 109 is with nm in the equivalence statement, we put 109 (or 1x109, same thing) with nm in the conversion factor. The 1 goes with the m.
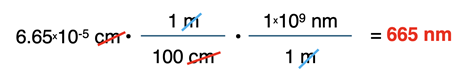
 To solve for the answer in nm, start with the given quantity (6.65x10-5) in your calculator and multiply by the two numerators (1 and 1x109) and divide by the two denominators (100 and 1). The result is 665 nm.
To solve for the answer in nm, start with the given quantity (6.65x10-5) in your calculator and multiply by the two numerators (1 and 1x109) and divide by the two denominators (100 and 1). The result is 665 nm.
If performing the calculation on a scientific calculator, you will need to be careful about entering values in exponential notation. To enter 1x109, you would tap on these buttons: 1, EE, and 9. You will never need to tap x10 (times 10). Tapping the EE button (or EXP button) is equivalent to tapping x10. The exponent of 9 can be entered after tapping EE.
Example 2
The distance for one lap around a typical high school track is ~0.25 mile. Determine the number of cm in 0.25 mile (mi).
Given: 1.609 km = 1 mi.
We once more begin by setting up the conversion factors with units only (no numbers). Starting with the given quantity – 0.25 mi – we will combine a few factors together consecutively until we acquire cm as the uncancelled unit. An understanding of how m is related to km (1000 m = 1 km) and of how cm is related to m (100 cm = 1m) was used to form the unit set up.

Once the conversion factors are set up, numbers are substituted into the numerators and denominators. The location of the numbers is based upon the equivalence statements. One equivalence statement is given (1.609 km = 1 mi). The other two (1000 m = 1 km and 100 cm = 1 m) were written from an understanding of the Greek prefixes of the metric system.

Once the numbers are in the right location, you can begin the calculation. Starting with 0.25 on your calculator, multiply by all the numerator values (*1.609 * 1000 * 100) and divide by all the denominator values (÷ 1 ÷ 1 ÷ 1). The final answer is rounded to the second significant digit and written in scientific notation. (Review the logic.) We will discuss more about significant digits and calculations in our next section of Lesson 4.
Example 3
Mercury has a density of 13.6 g/mL. Convert this value to kg/m3. Given: 1000 L = 1 m3.
Our final example includes a compound unit. A compound unit is a unit that includes more than one unit measure. Examples include mi/hr or m/s or kg/m3. This question involves the conversion of a numerical value in g/mL to kg/m3. That’s two units in the given quantity – grams (g) and milliliter (mL). You can think of this as involving two conversions. The g must be converted to kg and the /mL must be converted to /m3.
When you see a compound unit like g/mL, you can interpret it to mean “g per 1 mL”. So, when you write the given quantity, you will write it as a fraction with 1 mL in the denominator. This is the first time we’ve seen such compound units. As you set up conversion factors, the mL in the denominator of the given quantity would be cancelled by placing a mL in the numerator of one of your conversion factors.
Once more, we start by setting up the conversion factors with units only (no numbers):

The given quantity is listed first with both numbers and units – 13.6 g/1 mL. The first conversion factor is designed to convert the g to kg. The second and third conversion factors are designed to convert the /mL of the given quantity to /m3. The uncancelled units are kg in the numerator and m3 in the denominator. Taken together, this is kg/m3.
Now numbers can be substituted into the conversion factors. The last conversion factor relies on the given equivalence statement - 1000 L = 1 m3. The first two conversion factors rely on the meaning of Greek prefixes kilo- and milli-.
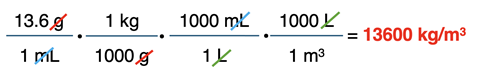
With the numbers are in the right location, you can begin the calculation. Starting with 13.6 on your calculator, multiply by all the numerator values (*1 * 1000 * 1000) and divide by all the denominator values (÷ 1000 ÷ 1 ÷ 1).
Before You Leave
- Practice does make perfect. Here’s three locations on the site where you can do some practice. You will get a problem. You solve and enter the answer. You tap the Submit button. Your answer is checked. If incorrect, you can make corrections. It's awesome practice.
The Calculator Pad, Problem Set UM2 – Unit Conversion 1
The Calculator Pad, Problem Set UM3 – Unit Conversion 2
The Calculator Pad, Problem Set UM4 – Unit Conversion 3
- You’ll find more practice below in the Check Your Understanding section:
Check Your Understanding
The use of conversion factors to perform metric conversions requires some practice. It’s time now to get out of your seat and turn this spectator sport into a participation sport. Show conversion factors to solve the following problems. Tap the Check Answer buttons when ready to view the answer and/or solution.
Convert:
- Bert Ticlychalanged is 45.3 cm tall. Not to make him feel worse, but how many kilometers tall is Bert?
- In PE class, Mr. Hintz measured the circumference of Ben Pumpiniron’s flexed biceps to be 34.8 inches. Given that 12 in = 1 ft and 3.28 ft = 1 m, calculate the circumference in millimeters.
- Suppose the Chemistry room has the dimensions 32.8 m x 3.6 m x 9.2 m. Calculate the volume of the room in m3. Use volume = L x H x W. Then use conversion factors to convert the volume to mL. Given: 1000 L = 1 m3.
- Lisa Corvette overslept this morning. She couldn’t stand to miss a minute of her first period Chemistry class. She was driving 72.5 mi/hr down Lake Avenue as she approached the light at Landwehr. Convert her speed to m/s. Given: 1609 m = 1 mi.