Sound and Music Review
Navigate to:
Review Session Home - Topic Listing
Sound Waves and Music - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-#9 || #10-#52 || #53-#64 || #65-#75
65. A guitar string has a fundamental frequency of 262 Hz. Determine the frequency of the ...
- ... second harmonic.
- ... third harmonic.
- ... fifth harmonic.
- ... eighth harmonic.
|
Answers:
The frequencies of the various harmonics of an instrument are whole number rations of the fundamental frequency. The frequency of the second harmonic is two times the fundamental frequency; the frequency of the third harmonic is three times the fundamental frequency and so on. The frequencies of the harmonics can be found utilizing the formula
fn = n * f1
a. f2 = 2 * f1 = 2 * 262 Hz = 524 Hz
b. f3 = 3 * f1 = 3 * 262 Hz = 786 Hz
c. f5 = 5 * f1 = 5 * 262 Hz = 1310 Hz
d. f8 =8 * f1 = 8 * 262 Hz = 2.10x 103 Hz
|
[ #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
66. Determine the speed of sound through air if the temperature is ...
- ... 0 degrees Celsius.
- ... 12 degrees Celsius.
- ... 25 degrees Celsius.
- ... 40 degrees Celsius.
|
Answers:
There are numerous equations for computing the speed of sound through air based on the temperature of air. A common equation found in books is
v = 331 m/s * SQRT (1 + T/273)
where T is the Celsius temperature. The following answers were found using this equation.
a. v = 331 m/s * SQRT (1 + 0/273) = 331 m/s
b. v = 331 m/s * SQRT (1 + 12/273) = 338 m/s
c. v = 331 m/s * SQRT (1 + 25/273) = 346 m/s
d. v = 331 m/s * SQRT (1 + 40/273) = 354 m/s
An alternative equation which is comonly used is v = 331 m/s + (.60 m/s/C)*T where T is the temperature is degrees celsius. Using this equation yields nearly the same same speed values - 331 m/s, 338 m/s, 346 m/s, and 355 m/s repsectively.
|
[ #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
67. A wind chime is an open-end air column. Determine the fundamental frequencies of a 62.5-cm chime when the temperature is ... .
- ... 12 degrees on a cold autumn evening.
- ... 25 degrees on a summer evening.
- ... 40 degrees during a hot summer day.
|
Answers:
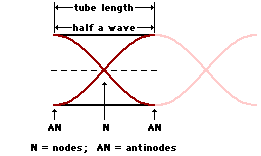 The frequency of the sound produced by a wind chime is related to the speed of air in the wind chime and the wavelength of the standing wave pattern of the resonating air column. The speed of the wave in air depends on the properties of air (temperature); these values were just computed in problem #66. The wavelength (lambda) of the resonating air column can be determined using a good diagram accompanied by the length of the air column. As depicted in the diagram at the right, the wavelength of the wave for the fundamental frequency is two times the length of the open-end air column. So in each of these cases, the wavelength is 2*62.5 cm = 125 cm = 1.25 m. With speed and wavelength known, the frequency values can be computed. The frequency of the sound produced by a wind chime is related to the speed of air in the wind chime and the wavelength of the standing wave pattern of the resonating air column. The speed of the wave in air depends on the properties of air (temperature); these values were just computed in problem #66. The wavelength (lambda) of the resonating air column can be determined using a good diagram accompanied by the length of the air column. As depicted in the diagram at the right, the wavelength of the wave for the fundamental frequency is two times the length of the open-end air column. So in each of these cases, the wavelength is 2*62.5 cm = 125 cm = 1.25 m. With speed and wavelength known, the frequency values can be computed.
a. f1 = v / lambda = (338 m/s) / (1.25 m) = 271 Hz
b. f1 = v / lambda = (346 m/s) / (1.25 m) = 277 Hz
c. f1 = v / lambda = (354 m/s) / (1.25 m) = 284 Hz
|
[ #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
68. An organ pipe has a length of 2.45 m and is open at both ends. Determine the fundamental frequency of the pipe if the temperature in the room is 25 degrees Celsius.
|
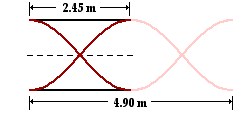 Answer: 70.6 Hz Answer: 70.6 Hz
For an open-end air column, the wavelength of the fundamental's standing wave pattern is two times the length of the air column; this relationship is depicted in the diagram at the right. So the wavelength of the wave is 4.90 m. The speed of the sound wave in air is dependent upon temperature. This speed was calculated in problem #66; it is 346 m/s. The frequency of the fundamental can now be calculated:
f1 = v / lambda
f1 = (346 m/s) / (4.90 m) = 70.6 Hz
|
[ #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
69. (Referring to problem #68.) Determine the fundamental frequency of the pipe if it is closed at one end.
|
Answer: 35.3 Hz
The easy way to solve this problem is to recognize that by changing an open end to a closed end has the effect of lengthening the wave by a factor of two. If the wavelength is twice as large, then the frequency is twice as small. Thus, divide the original answer of 70.6 Hz (question #68) by 2.
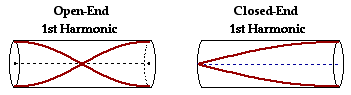
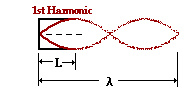
Alternatively, one could repeat the entire process of re-computing the wavelength from a diagram of the standing wave of the fundamental in a closed-end air column. For the fundamental, the wavelength is four times the length of the air column. In this case, the wavelength would be 9.80 m. Now divide the speed of the sound wave (346 m/s) by the wavelength value to obtain the frequency.
|
[ #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
70. The auditory canal of the outer ear acts as a closed end resonator which has a natural frequency of around 3500 Hz. This canal serves to amplify sounds with frequencies around this value, thus making us more sensitive to such frequencies. If the speed of waves inside the canal is 350 m/s, then what is the estimated length of the canal?
|
Answer: 2.5 cm
For closed end resonators, the standing wave patterns of the natural frequencies are characterized by a node at the closed end and an antinode at the open end. For the first harmonic (and it must be assumed that the 3500 Hz corresponds to the first harmonic), the wavelength is four times the length of the air column. The strategy in this problem involves determining the wavelength (lambda) from the speed and the frequency and then determining the length from the wavelength-length relationship.
lambda = v / f = (350 m/s) / (3500 Hz) = 0.1 m
L = 0.25 * lambda = 0.25 * (0.1 m) = 0.025 m = 2.5 cm
|
[ #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
71. Determine the frequency of the lowest three harmonics at which a closed-end air column would sound out at 25 degrees Celsius if its length is 135 cm.
|
Answer: 64.0 Hz, 192 Hz, 320 Hz
The fundamental frequency of a closed-end air column is characterized by a standing wave pattern in which there is a node at the closed end and an antinode at the open end. There is one-fourth of a wavelength present within the length of the tube; thus, the wavelength is four times the length. In the case of this air column, the wavelength of the first harmonic is
lambda1 = 4*135 cm = 540 cm = 5.40 m
The speed of sound waves in air at 25 degree Celsius was computed in problem #66 to be 346 m/s. The frequency of the first harmonic can now be calculated from the speed and the wavelength.
f1 = v / lambda1 = (346 m/s) / (5.40 m) = 64.0 Hz
The next two lowest frequencies are the third and the fifth harmonics. (Recall the closed-end air columns do not have even-numbered harmonics.) The frequencies of these harmonics are multiples of the first harmonic frequency.
f3 = 3 * f1 = 3 * 64.0 Hz = 192 Hz
f5 = 5 * f1 = 5 * 64.0 Hz = 320 Hz
|
[ #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
72. Suppose that a sound is produced in a helium-filled air column rather than an air-filled air column. By what factor will this change in medium alter the frequency of the sound. (GIVEN: vair = 331 m/s; vHe = 970 m/s)
|
Answer: 2.93
The frequency of a resonating air column is dependent upon the speed of sound in that air column; the relationship is a direct relationship. If the air is replaced by another gas that transmits sound waves with a different speed, then the frequency will be increased by the same factor by which the speed is increased. In this problem, the speed of sound is increased by a factor of
Factor = (970 m/s) / (331 m/s) = 2.93
Thus, the frequency is increased by a factor of 2.93.
|
[ #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
73. An organ pipe is used to produce the lowest note audible to the human ear - 20.-Hz. If the temperature is 25 °C, then how long is the organ pipe? (First decide whether it will produce this low note as a closed- or as an open-end air column.)
|
Answer: 4.3 m
Harmonics produced by closed-end air columns are characterized by longer wavelengths than the harmonics of open-end air columns of the same length. Thus, a closed-end air column produces lower frequencies. For this reason, we'll assume that the organ pipe in this problem is a closed-end air column. (Note, your answer will be two times larger if you assumed this to be an open-end air column.)
At a temperature of 25°C, sound waves travel at 346 m/s (see problem #66). The frequency and speed can be used to determine the wavelength (lambda):
lambda = v / f = (346 m/s) / (20 Hz) = 17.3 m
The wavelength of the first harmonic of a closed-end air column is four times the length of the column; so the length of the column is one-fourth the wavelength.
L = 0.25 * 17.3 m = 4.3 m
|
[ #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
74. Determine the length of an open-end air column which would produce a 262 Hz frequency on a balmy day when the temperature is 12 degrees.
|
Answer: 64.5 cm
The speed of sound waves at 12 °C is 338 m/s (see problem #66). The wavelength (lambda) of a 262 Hz sound at this temperature is
lambda = v / f = (338 m/s) / (262 Hz) = 1.29 m
For an open-end air column, the wavelength of the first harmonic is two times the length of the air column. So the length is one-half the wavelength:
L = 0.5 * 1.29 m = 0.645 m = 64.5 cm
|
[ #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
75. A 440.-Hz tuning fork is held above the open end of a water-filled pop bottle and resonance is heard. The length of the pop bottle (bottom to top) is 28.2 cm. If the speed of sound is 345 m/s, then to what height is the pop bottle filled with water?
|
Answer: 19.6 cm
The wavelength (lambda) of a 440 Hz sound can be determine from the wave equation (v = f*lambda)
lambda = v / f = (345 m/s) / (440. Hz) = 0.784 m
For a closed-end air column, the wavelength of the first harmonic is four times the length of the air column. So the length is one-fourth the wavelength:
L = 0.25 * 0.784 m = 0.196 m = 19.6 cm
If the pop bottle is 28.2 cm tall, then it should be filled with 8.6 cm of water in order for there to remain 19.6 cm of air.
|
[ #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
Navigate to:
Review Session Home - Topic Listing
Sound Waves and Music - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-#9 || #10-#52 || #53-#64 || #65-#75
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Sound and Music
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 5 of the series includes topics on Sound Waves and Music.
Visit: MOP the App Home || MOP the App - Part 5