21.
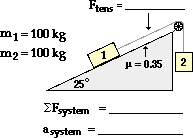
Like #20, this problem can most easily be solved using separate free-body analyses on the individual masses. Free-body diagrams, the chosen axes systems, and associated information is shown below. Note that in chosing the axis system, it has been assumed that object 1 will accelerate up the hill and object 2 will accelerate downwards. If this ends up to be false, then the acceleration values will turn out to be negative values.
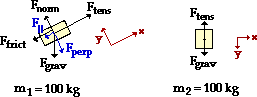
Object 1 is on an inclined plane. The usual circumstances apply; their is no acceleration along what has been designated as the y-axis.
Fnorm = Fperp = m•g•cos(theta) = 888.2 N
The parallel component of Fgrav is
F|| = m•g•sin(theta) = (100 kg)•(9.8 m/s2)•sin(25)
F|| = 414.2 N
The Ffrict value can be found from the Fnorm value:
Ffrict = mu•Fnorm = (0.35)•(888.2 N) = 310.9 N
The ∑Fx = m•ax equation can now be written:
∑Fx = m•ax
Ftens - Ffrict - F|| = m•ax
 Ftens - 310.9 N - 414.2 N = m•ax
Ftens - 310.9 N - 414.2 N = m•ax
(Note that the Ffrict and F|| forces are subtracted from Ftens since they are heading in the direction of the negative x-axis.)
The above process can be repeated for object 2. The ∑Fy = m•ay equation can now be written:
∑Fy = m•ay
Fgrav - Ftens = m•ay
 (980 N) - Ftens = m•ay
(980 N) - Ftens = m•ay
The separate free-body analyses have provided two equations with two unknowns; the task at hand is to use these two equations to solve for Ftens and a.
Equation 2 can be re-written as
(980 N) - m•ay = Ftens
Since both objects accelerate together at the same rate, the ax for object 1 is equal to the ay value for object 2. The subscripts x and y can be dropped and a can be inserted into each equation.
 (980 N) - m•a = Ftens
(980 N) - m•a = Ftens
Equation 3 provides an expression for Ftens in terms of a. This expression is inserted into equation 1 in order to solve for acceleration. The steps are shown below.
(980 N) - m•a - 310.9 N - 414.2 N = m•a
= 2•m•a
254.9 N = 2•(100 kg)•a
1.27 m/s2 = a
The value of a can be re-inserted into equation 3 in order to solve for Ftens:
Ftens = (980 N) - m•a =(980 N) - (100 kg)•(1.27 m/s2)
Ftens = 853 N