Ray Optics: Refraction and Lenses
Refraction and Lenses: Problem Set Overview
There are 20 ready-to-use problem sets on the topic of Refraction and Lenses. The problems target your ability to mathematically relate the index of refraction and the light speed, to use Snell's Law and (at times) trigonometric principles to analyze physical situations regarding light refraction, to determine critical angles and to use the lens equation and magnification ratio to solve lens problems. Problems range in difficulty from the very easy and straight-forward to the very difficult and complex.
Light Speed and the Index of Refraction
The speed of a light ray is dependent upon the medium through which it travels. Light travels relatively slowly in a more optically dense material and faster in less optically dense materials. The index of refraction value (n) provides a direct measure of the optical density of a material. It can be used to relate the speed of light in that material (v) to the speed of light in a vacuum (c = 3.0 x 108 m/s). The speed of light equation is stated above; it can be used to relate light speed to index of refraction values. A more detailed and exhaustive discussion of optical density, light speed and the index of refraction can be found at The Physics Classroom Tutorial.
Angles of Incidence and Refraction
The angle of incidence value is the angle measure between the incident ray and the normal line. The normal line is an imaginary line drawn perpendicular to the boundary at the location where the incident ray strikes the boundary. The angle of refraction value is defined in a similar manner; it is the angle measure between the refracted ray and the normal line. Making these measurements simply involves the placement of a protractor along the boundary with its origin placed at the location where the light ray strikes the boundary. A more detailed and exhaustive discussion of the angles of incidence and refraction can be found at The Physics Classroom Tutorial.
Snell's Law of Refraction
A light ray will undergo refraction (a change in direction of its path) at a boundary between two materials whenever it approaches the boundary at an angle of incidence other than zero degrees. This refraction occurs in a rather predictable manner as expressed by the Snell's law equation:
n1 • sin ( θ1 ) = n2 • sin (θ2)
where n1 = index of refraction value of material 1 (on one side of the boundary)
n2 = index of refraction value of material 2 (on the opposite side of the boundary)
θ1 = angle of refraction of material 1 (on one side of the boundary)
θ2 = angle of refraction of material 2 (on the opposite side of the boundary)
Knowing the index of refraction values of the two materials on opposite sides of the boundary and the angle of incidence allows one to make a calculation of the angle of refraction. In a similar manner, knowing the two angles that a light ray makes with the normal line for both sides of the boundary and knowing one of the index of refraction values of the two materials allows one to determine the second index of refraction value.
Trigonometric Relationships
There is a unique relationship between the angles within a right triangle and the ratio of the length of the sides. Trigonometric functions are mathematical functions that relate the length of the sides of a right triangle to the angles within the triangle.
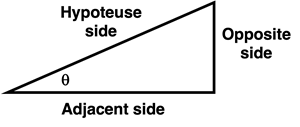 Any triangle has three angles. A right triangle has two acute angles and one right angle. Trigonometric functions are typically used to express the relationship between the measure of one of the acute angles and the ratio of the length of the sides. Each of the acute angles is formed by the intersection of one of the short sides and the hypotenuse side of the triangle. The short sides are often referred to as the adjacent side and the opposite side. The adjacent side is the side that when combined with the hypotenuse side forms a specific angle. The side of the triangle that is located along the triangle opposite of this specified angle is the opposite side.
Any triangle has three angles. A right triangle has two acute angles and one right angle. Trigonometric functions are typically used to express the relationship between the measure of one of the acute angles and the ratio of the length of the sides. Each of the acute angles is formed by the intersection of one of the short sides and the hypotenuse side of the triangle. The short sides are often referred to as the adjacent side and the opposite side. The adjacent side is the side that when combined with the hypotenuse side forms a specific angle. The side of the triangle that is located along the triangle opposite of this specified angle is the opposite side.
The sine function relates the angle measure of one of the acute angles to the ratio of the lengths of the side opposite the angle and the length of the  hypotenuse. The cosine function relates the angle measure of one of the acute angles to the ratio of the lengths of the side adjacent the angle and the length of the hypotenuse. And finally the tangent function relates the angle measure of one of the acute angles to the ratio of the lengths of the side opposite the angle and the length of the side adjacent the angle. The meaning of the functions can be easily remembered by the catchy mnemonic
hypotenuse. The cosine function relates the angle measure of one of the acute angles to the ratio of the lengths of the side adjacent the angle and the length of the hypotenuse. And finally the tangent function relates the angle measure of one of the acute angles to the ratio of the lengths of the side opposite the angle and the length of the side adjacent the angle. The meaning of the functions can be easily remembered by the catchy mnemonic
SOH CAH TOA
The equations defining these functions are listed at the right.
In Physics, there are numerous physical situations in which a student would want to relate the angle in a right triangle to the length of one or more of its sides. In such instances, a trigonometric function is chosen and used to analyze the physical situation. For instance, the refraction of light at a boundary causes the angle that the light path makes with the normal (and also with the boundary) to change. It is different on one side of the boundary than on the other side of the boundary. If this light path is projected 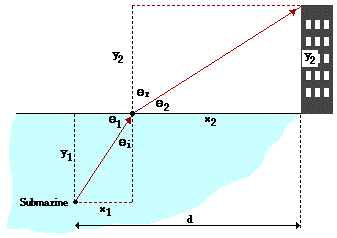 through space on either side of the boundary it will likely strike a physical object. There is subsequently a triangle (or even a pair of triangles) formed by the boundary, the light ray and physical objects present in the vicinity.
through space on either side of the boundary it will likely strike a physical object. There is subsequently a triangle (or even a pair of triangles) formed by the boundary, the light ray and physical objects present in the vicinity.
This is best illustrated in the diagram at the right. Laser light is sent from a submarine at an angle to the water surface. The light refracts at the boundary and strikes the top of a tall building on the water's edge. Refraction principles can be used to relate the angle of incidence (Θi) to the angle of refraction (Θr). These angles are in turn related to the distance measurements shown on the diagram.
As a discipline concerned about the relationships present in the physical environment, physics is clearly interested in questions concerning dimensions, directions, angle measures and the like. These three trigonometric functions, when combined with physics principles such as Snell's Law, allows one to make quantitative predictions and conclusions concerning the dimensions and angles associated with the origin and the destination of the path of a light ray.
Total Internal Reflection and The Critical Angle
Upon reaching a boundary, a light ray will undergo partial reflection and partial transmission. The transmitted light will change its direction whenever it approaches the boundary at any angle of incidence other than 0 degrees. The reflected ray simply reflects according to the law of reflection; that is, the angle of reflection is equal to the angle of incidence. There are instances however when the incidence light does not follow the usual rule of partial reflection and partial transmission. In such instances, all the light which approaches the boundary will undergo reflection and stay within the original medium. This phenomenon is referred to as total internal reflection and occurs whenever the following two criteria are met:
- Light is in the more dense medium and heading toward the less dense medium.
- Light is approaching the boundary at an angle of incidence that is greater than a critical angle value.
The critical angle is the angle of incidence that causes light to refract along the boundary at an angle of refraction of 90 degrees. Since 90 degrees is the largest possible angle of refraction, an incident ray with an angle of incidence greater than the critical angle cannot refract. Such a light ray will only reflect and stay within the original medium. Using Snell's law, one can show that the critical angle can be calculated from the index of refraction values of the two media on both sides of the boundary. The formula is
Θcritical = sin-1 ( n2 / n1 )
where n1 represents the index of refraction of the incident medium and n2 represents the index of refraction of the refractive medium. In order for total internal reflection to occur, the value of n2 must be greater than the value of n1. This restriction is consistent with the criteria that light be in the more dense medium and heading towards the less dense medium.
A more detailed and exhaustive discussion of total internal reflection and the critical angle can be found at The Physics Classroom Tutorial.
The Mathematics of Lenses
Many of the problems within this problem set pertain to converging and diverging lenses. For these problems, you will make frequent use of two equations - the lens equation and the magnification equations. These equations are shown below:
|
Lens Equation
1 / f = 1/ do + 1 / di
|
Magnification Ratio
M = hi / ho = - di / do
|
In the above equations, the variable do represents the object distance or the distance between the lens and the object. The variable di represents the image distance or the distance between the lens and the image. The variable ho represents the object height and the variable hi represents the image height. The variable f stands for the focal length of the lens. The variable M stands for the magnification of the image; it represents how many times bigger the image is than the object.
These equations are used to assist in the solution of physics word problems. Values of two or more quantities are typically expressed in the problem; the goal of the word problem is to solve for an unknown quantity. Known quantities of the variables must be substituted into the above equations and proper algebraic manipulations must be performed in order to solve for the unknown variable.
Sign Conventions Used in Lens Problems
Perhaps one of the most problematic areas of lens problems is dealing with the sign conventions associated with the image distance, focal length and image height. The table below summarizes the sign conventions associated with these quantities.
|
Quantity
|
Sign Convention
|
|
do
|
For our purposes, the object distance (do) will always be positive.
|
|
ho
|
For our purposes, the object height (ho) will always be positive.
|
|
di
|
A positive image distance (di) corresponds to an image location on the opposite side of the lens as the object. A negative image distance (di) corresponds to an image located on the same side as the lens as the object. Thus, all real images have positive image distances and all virtual images have negative image distances.
|
|
hi
|
A positive image height (hi) corresponds to an upright image. A negative image height (hi) corresponds to an inverted image. All upright images (positive hi values) are virtual images located on the object's side of the lens; upright images will thus be virtual images with negative di values. Likewise, inverted images with their negative hi values are real images that have positive di values.
|
|
f
|
A converging lens will have a positive focal length (f) and a diverging lens will have a negative focal length (f).
|
|
M
|
Magnification values are positive whenever image heights (hi) are positive. Thus, positive M values correspond to upright, virtual images located on the object's side of the lens. Conversely, negative M values correspond to inverted, real images located on the side of the lens opposite of the object.
|
When reading a problem, give attention to cues within the problem in order to determine the sign on the given quantity. For instance, a problem may describe an object located to the left of a diverging lens and a virtual image located to the left of the diverging lens. Applying the above conventions, one can assign a positive value to the object distance and a negative value to the image distance. Failure to recognize such small nuances of problems will result in wrong answers despite the accuracy of the mathematical manipulations. A careful reading of the problem statement along with an understanding of the sign conventions (as stated in the table above) for the variables within the two equations allows one to make proper conceptual decisions. These types of decisions are critical to your success on these problems. Making the correct decisions has nothing to do with your mathematical skills. Rather, they are tests of your conceptual understandings and your willingness to read a problem carefully and to give attention to details which may be important.
Solving Complex Problems with Systems of Simultaneous Equations
There are several instances in these problems in which the lens equation must be used to solve for an unknown variable but only one of the other two variable values are known. Such problems usually have a statement of the effect: "the image is real and three times the size of the object." Such a statement reveals information about the magnification of the image. Since the ratio of the image to object height is equal to the (negative of the) ratio of the image distance to object distance, we can say that size and height can be treated synonymously. Stating that the image is three times the size of the object is stating that the ratio hi/ho is either +3 or -3. Determining whether hi/ho is +3 or -3 demands an understanding of the sign conventions (as discussed in the above table). The ho value is always positive (for our purposes). The hi value is positive for upright images and negative for inverted images. Since this statement asserts that the image is real (and thus inverted), a -3 value must be assigned to the hi/ho ratio. Since hi/ho is equal to -di/do, the -3 value can be equated with -di/do. This stream of logic allows one to write an expression for di in terms of do. This expression for di in terms of do can be substituted into the lens equation in order to transform it into a single equation with a single unknown. Customary algebraic manipulations can then be performed in order to solve for di or for do.
The table below summarizes the process of transforming a verbal statement into a mathematical equation which ultimately is used to substitute into the lens equation.
|
Verbal Statement
|
Mathematical Equivalent
|
Expression of di in terms of do
|
|
"... the image is real and three times the size of the object."
|
hi / ho = -3 = -di / do
|
di = +3do
or do = (+1/3)•di
|
Habits of an Effective Problem-Solver
An effective problem solver by habit approaches a physics problem in a manner that reflects a collection of disciplined habits. While not every effective problem solver employs the same approach, they all have habits which they share in common. These habits are described briefly here. An effective problem-solver...
- ...reads the problem carefully and develops a mental picture of the physical situation. If needed, they sketch a simple diagram of the physical situation to help visualize it.
- ...identifies the known and unknown quantities and records them in an organized manner. Equates given values to the symbols used to represent the corresponding quantity - e.g., do = 24,8 cm; di = 16.7 cm; f = ???.
- ...plots a strategy for solving for the unknown quantity; the strategy will typically center around the use of physics equations and be heavily dependent upon an understanding of physics principles.
- ...identifies the appropriate formula(s) to use, often times writing them down. Where needed, they perform the needed conversion of quantities into the proper unit.
- ...performs substitutions and algebraic manipulations in order to solve for the unknown quantity.
Read more...
Additional Readings/Study Aids:
The following pages from The Physics Classroom tutorial may serve to be useful in assisting you in the understanding of the concepts and mathematics associated with these problems.