Mechanics: Circular Motion and Gravitation
Circular Motion and Gravitation: Problem Set Overview
The set of problems on this topic targets your ability to combine Newton's laws and circular motion and gravitation equations in order to analyze the motion of objects moving in circles, including orbiting satellites. Problems range in difficulty from the very easy and straight-forward to the very difficult and complex.
Motion Characteristics of Objects Moving in Circles
Objects moving in circles have a speed that is equal to the distance traveled per time of travel. The distance around a circle is equivalent to a circumference and calculated as 2•π•R where R is the radius. The time for one revolution around the circle is referred to as the period and denoted by the symbol T. Thus the average speed of an object in circular motion is given by the expression 2•π•R / T. Often times the problem statement provides the rotational frequency in revolutions per minute or revolutions per second. Each revolution around the circle is equivalent to a circumference of distance. Thus, multiplying the rotational frequency by the circumference allows one to determine the average speed of the object.
The acceleration of objects moving in circles is based primarily upon a direction change. The actual acceleration rate is dependent upon how rapidly the direction is being changed and is directly related to the speed and inversely related to the radius of the turn. It ends up that the acceleration is given by the expression v2 / R where v is the speed and R is the radius of the circle.
The equations for average speed (v) and average acceleration (a) are summarized below.
v = d / t = 2•π•R / T = frequency • 2•π•R
a = v2 / R
Directional Quantities for Objects Moving in Circles
A successful mathematical analysis of objects moving in circles is heavily dependent upon a conceptual understanding of the direction of the acceleration and net force vectors. Movement along a circular path requires a net force directed towards the center of the circle. At every point along the path, the net force must be directed inwards. While there may be an individual force pointing outward, there must be an inward force which overwhelms it in magnitude and meets the requirement for an inward net force. Since net force and acceleration are always in the same direction, the acceleration of objects moving in circles must also be directed inward.
Free Body Diagrams and Newton's Second Law
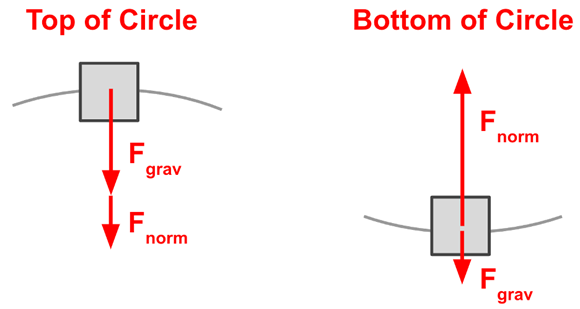
Often times a force analysis must be conducted upon an object moving in circular motion. The goal of the analysis is either to determine the magnitude of an individual force acting upon the object or to use the values of individual forces to determine an acceleration. Like any force analysis problem, these problems should begin with the construction of a free-body diagram showing the type and direction of all forces acting upon the object. From the diagram, an Fnet = m•a equation can be written. When writing the equation, recall that the Fnet is the vector sum of all the individual forces. It is best written by adding all forces acting in the direction of the acceleration (inwards) and subtracting those which oppose it. Two examples are shown in the graphic below.
Newton's Law of Universal Gravitation
Orbiting satellites are simply projectiles - objects upon which the only force is gravity. The force that governs their motion is the force of gravitational attraction to the object that is at the center of their orbit. Planets orbit the sun as a result of the gravitational force of attraction to the sun. Natural moons orbit planets as a result of the gravitational force of attraction to the planet. Gravitation is a force that acts over large distances in such a manner that any two objects with mass will attract. Newton was the first to propose a theory to describe this universal mass attraction and to express it mathematically. The law, known as the law of universal gravitation states that the force of gravitational attraction is directly proportional to the product of the masses and inversely proportional to the square of the separation distance between their centers. In equation form,
Fgrav = G • m1 • m2 / d2
where m1 and m2 are the masses of the attracting objects (in kg) and d is the separation distance as measured from object center to object center (in meters) and G is the proportionality constant (sometimes referred to as the universal gravitation constant). The value of G is 6.673 x 10-11 N•m2/kg2.
Learn more with our video titled Newton's Law of Universal Gravitation.
Acceleration of Gravity
Since orbiting satellites are acted upon solely by the force of gravity, their acceleration is the acceleration due to gravity (g). On earth's surface, this value was 9.8 m/s2. For locations other than Earth's surface, there is a need for an equation which expresses g in terms of relevant variables. The acceleration of gravity depends upon the mass of the object which is at the center of the orbit (Mcentral) and the separation distance from that object (d). The equation which relates these two variables to the acceleration of gravity is derived from Newton's law of universal gravitation. The equation is
g = G • Mcentral / d2
where G is 6.673 x 10-11 N•m2/kg2. Our video titled The Value of g treats this topic in greater detail.
Orbital Speed
The speed required of a satellite to remain in a circular orbit about a central body (planet, sun, other star, etc.) is dependent upon the radius of orbit and the mass of the central body. The equation expressing the relationship between these variables is derived by combining circular motion definitions of acceleration with Newton's law of universal gravitation. The equation is
v = SQRT (G • Mcentral / R)
where Mcentral is the mass of the central body about which the satellite orbits, R is the radius of orbit and G is 6.673 x 10-11 N•m2/kg2. Learn how to use this equation as a guide to thinking and recipe for problem-solving with our video titled Satellite Motion Mathematics.
Orbital Period
For the general motion of an object in a circle, the period is related to the radius of the circle and the speed of the object by the equation v = 2 • π • R / T. In the case of an orbiting satellite, this equation for speed can be equated with the equation for the orbital speed derived from universal gravitation to derive a new equation for orbital period. The result of the derivation is
T2 / R3 = 4 • π2 / (G • Mcentral )
where Mcentral is the mass of the central body about which the satellite orbits, R is the radius of orbit and G is 6.673 x 10-11 N•m2/kg2. Expressed in this manner, the equation shows that the ratio of period squared to the radius cubed for any satellite that is orbiting a central body is the same regardless of the nature of the satellite or the radius of its orbit. This ratio is only dependent upon the mass of the object which pulls the orbiting satellite inward. This principle is consistent with as Kepler's third law of planetary motion.
Learn how to use this equation as a guide to thinking and recipe for problem-solving with our video titled Kepler's Three Laws of Planetary Motion.
Summary of Mathematical Formulas
One difficulty a student may encounter with this topic is the confusion as to which formula to use. The table below provides a useful summary of the formulae pertaining to circular motion and satellite motion. In the table, many of the formulae were derived from other equations. Thus, there will often be more than one means of determining an unknown quantity. In approaching these problems, it is suggested that you practice the usual habits of an effective problem-solver; identify known and unknown quantities in the form of the symbols of physics formulas, plot out a strategy for using the knowns to solve for the unknown, and then finally perform the necessary algebraic steps and substitutions required for the solution.
| To calculate ... |
... use the equation(s): |
Speed
(v) |
v = 2 • pi • R / T
v = SQRT (G • Mcentral / R) for satellites only |
Acceleration
(a) |
a = v2 / R or a = Fnet / m
a = g = G • Mcentral / d2 for satellites only |
Net force
(Fnet) |
Fnet = m • a or Fnet = m • v2 / R
Fnet = Fgrav = G • msat • Mcentral / d2 for satellites only |
Period
(T) |
T = 2 • pi • R / v
T2 = 4 • pi2 / (G • Mcentral ) • R3 for satellites only |
Habits of an Effective Problem-Solver
An effective problem solver by habit approaches a physics problem in a manner that reflects a collection of disciplined habits. While not every effective problem solver employs the same approach, they all have habits that they share in common. These habits are described briefly here. An effective problem-solver...
- ...reads the problem carefully and develops a mental picture of the physical situation. If needed, they sketch a simple diagram of the physical situation to help visualize it.
- ...identifies the known and unknown quantities in an organized manner, often times recording them on the diagram itself. They equate given values to the symbols used to represent the corresponding quantity (e.g., m = 61.7 kg, v= 18.5 m/s, R = 30.9 m, Fnorm = ???).
- ...plots a strategy for solving for the unknown quantity; the strategy will typically center around the use of physics equations and be heavily dependent upon an understanding of physics principles.
- ...identifies the appropriate formula(s) to use, often times writing them down. Where needed, they perform the needed conversion of quantities into the proper unit.
- ...performs substitutions and algebraic manipulations in order to solve for the unknown quantity.
Read more...
Additional Readings/Study Aids:
The following pages from The Physics Classroom tutorial may serve to be useful in assisting you in the understanding of the concepts and mathematics associated with these problems.
Watch a Video
We have developed and continue to develop Video Tutorials on introductory physics topics. You can find these videos on our YouTube channel. We have an entire Playlist on the topic of Circular Motion and Gravitation.