Chemistry: Stoichiometry of Reactions
Stoichiometry: Problem Set Overview
We have 16 ready-to-use problem sets on the topic of Stoichiometry. These problem sets focus on the use of the coefficients of a balanced chemical equation and molar mass values to relate the amount of reactants and products involved in a chemical reaction. Problems will range from the very easy mole-to-mole calculations to the more difficult limiting reactant problems.
Balanced Chemical Equations
Chemical reactions are described by a balanced chemical equation. The equation identifies the reactants and the products in terms of their chemical formulas. The equation also uses coefficients to describe the relative number of particles of reactants and products that are participating in the reaction. The balanced chemical equation for the synthesis of ammonia (NH3) from its elements is
N2 + 3 H2 → 2 NH3
There are two obvious coefficients in this balanced chemical equation (the 3 in front of H2 and the 2 in front of NH3) and one implied coefficient (the 1 in front of N2). This balanced chemical equation is describing the chemical reaction in the following way:
1 molecule of nitrogen react with 3 molecules of hydrogen to produce 2 molecules of ammonia.
And we could also say ...
2 molecules of nitrogen react with 6 molecules of hydrogen to produce 4 molecules of ammonia
or even ...
10 molecules of nitrogen react with 30 molecules of hydrogen to produce 20 molecules of ammonia
or even ...
6.022x1023 molecules of nitrogen react with 18.066x1023 molecules of hydrogen to produce 12.044x1023 molecules of ammonia.
With a balanced chemical equation, there is an endless number of ways by which we could accurately describe the quantities of reactants and products involved in the reaction. But in the case of this reaction, all those ways will include amounts that follow the ratio of 1:3:2 with respect to N2, H2, and NH3.
The balanced chemical equation is basis for stoichiometry ... the topic of this unit at The Calculator Pad. Stoichiometry is the study of the quantitative relationships or ratios between substances involved in a chemical reaction. Since the coefficients of the balanced chemical equation identifies the ratios by which the particles of reactants and products are involved, it forms the foundation upon which stoichiometry is practiced. And the big take-home from this idea is that a student of chemistry cannot do stoichiometry without either a balanced chemical equation or a whole heaping amount of luck. Needless to say, its better to rely on a balanced chemical equation than on luck.
Mole-to-Mole Stoichiometry
You might recall from a previous unit that the mole is a counting unit in much the same way that a pair, a dozen, or a gross is a counting unit. While a pair describes a grouping of 2 items and a dozen describes a grouping of 12 items, a mole describes a grouping of 6.022 x 1023 items. It is used in Chemistry since the samples of reactants and products typically include a large (like, really large) quantity of particles. And since we can use the coefficients of a balanced chemical equation to describe the ratios by which reactant and product particles participate in chemical reactions, we can just as easily express our descriptions in terms of moles. So for instance, the balanced chemical equation ...
N2 + 3 H2 → 2 NH3
describes a reaction in which
1 mole of nitrogen reacts with 3 moles of hydrogen to produce 2 moles of ammonia.
The 1, the 3, and the 2 in the balanced equation and in the verbal description describes the simplest ratio by which these three substances participate in the reaction. They indicate the following stoichiometric truths:
- The reaction will always require three times as many moles of hydrogen as moles of nitrogen.
- The reaction will always produce two times as many moles of ammonia as moles of nitrogen.
- The reaction will always produce two-thirds as many moles of ammonia as moles of hydrogen.
Put another way, the stoichiometric ratio of nitrogen to hydrogen is 1:3. The stoichiometric ratio of nitrogen to ammonia is 1:2. And the stoichiometric ratio of hydrogen to ammonia is 3:2. These ratios can be used to determine the moles of reactants and products involved with one another when solving a so-called mole-to-mole stoichiometry problem. As was stated above, the balanced chemical equation forms the basis of stoichiometry.
Review: Grams-to-Moles Conversions
In a previous unit of The Calculator Pad, we learned that the molar mass of a substance indicates the mass of one mole of particles of that substance. The molar mass can be determined from the formula for a substance using atomic mass values found on the Periodic Table. The units for molar mass are grams per mole or g/mol.
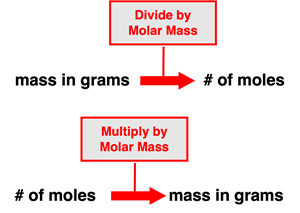The mass of a sample of a substance (element or compound) is related to the number of moles of that substance within the sample. The molar mass of a substance describes the mass in grams of one mole of particles of that substance. So when we say the substance carbon dioxide (CO2) has a molar mass of 44.01 g/mol, we mean that a mole of CO2 molecules would have 44.01 grams of mass. And so the molar mass becomes a means of converting between the grams of a substance and the number of moles of a substance. Converting the mass of a substance in grams to the number of moles involves dividing by the molar mass. And converting the number of moles of a substance to the mass in grams involves multiplying by the molar mass. We can think of such conversions as involving a single step of multiplication or division.
Two Steps: Grams-to-Moles-to-Moles Stoichiometry
The molar mass provides a means of converting between the number of moles of a substance and the mass of a substance. Such conversions can be incorporated into a stoichiometric analysis of a chemical reaction in order to relate the masses of reactants and products involved in the reaction. While the coefficients of the chemical equation relate the moles of participating reactants and products, the molar mass values relate the moles of a substance to the mass of that very same substance.
This principle can be used in the solution of problems that provide the mass of a reactant (or a product) and request that the moles of another reactant or of a product be determined. Such problems can be thought of as two step problems. First, a molar mass value is used to convert from the given mass (usually in grams) of the reactant to the number of moles of that very reactant. And second, the coefficients are used to convert from the moles of the reactant determined in the first step to the moles of the other reactant or of a product. Put together, these two steps allow one to perform a mass to mole to mole conversion. The following schematic shows the pathway from the given quantity to the requested quantity.
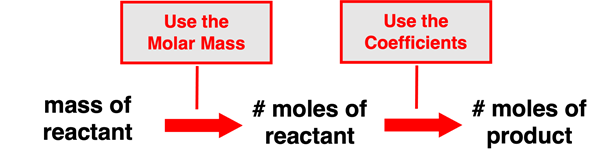
A similar process can be used if a problem provides the moles of a reactant or of a product in the reaction and requests that the mass of another reactant or product be determined. This is a slight variation of the previous problem. It also involves two steps. The first step involves using the coefficients of the balanced equation to convert from the moles of the given substance to the moles of a second substance. The second step involves using the molar mass value to convert from the moles of the second substance to the mass (in grams) of the second substance. This can be described as a mole to mole to mass conversion. The schematic shows the pathway from the given quantity to the requested quantity.
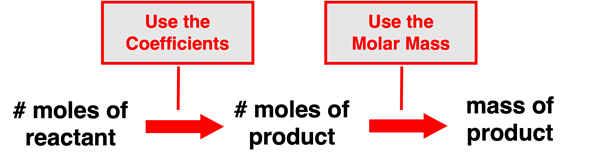
Using the Factor-Label Method
The factor-label method was introduced in our Units and Measurement unit at The Calculator Pad. The factor-label method makes use of converting factors (a.k.a., conversion factors) to convert from one quantity to antoher quantity. In many courses, the factor-label method is required when doing stoichiometric calculations. And in our opinion, the factor-label method is an essential tool in the toolbox of a chemistry student who is attempting to work through a stoichiometry problem. Reliance on the use of conversion factors becomes more critical as the problems become more complex.
The factor-label method is a unit-cancellation method used to convert from a quantity in one set of units to another set of units. The units are primary; the numbers are secondary. To illustrate its use, consider the reaction
N2 + 3 H2 → 2 NH3
and the task of determining the moles of NH3 produced from the reaction of 12.9 g of H2. We know from our understanding of molar mass that 2.016 g of H2 is equivalent to 1.000 mol of H2. And we know from our understanding of balanced chemical equations that 3.000 moles of H2 is an equivalent amount of reactant to produce 2.000 mole of NH3. From these two bits of information, we can create the following converting factors.
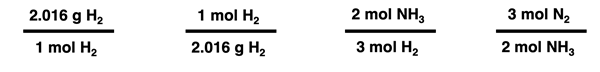
Two of these converting factors can be used to convert from the 12.9 g H2 to the number of moles of NH3 produced. The ones which are chosen can be determined by focusing on units and unit cancellation. A unit in a numerator can be cancelled by placing the identical unit in the denominator of the next conversion factor. And a unit in a denominator can be cancelled by placing the identical unit in the numerator. The given quantity - 12.9 g H2 - can be treated as a numerator. And so the following string of two converting factors (without numbers) can be utilized to cancel units.
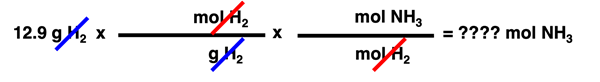
As shown above, the first converting factor is used to cancel the g H
2. That would leave the mol H
2 in the numerator. So the second converting factor is used to cancel the mol H
2.
It is wise to focus on units when using the factor-label method. Begin by setting up converting factors with units and no numbers as shown above. Where the actual numbers are inserted - whether in the numerator or denominator - won't be evident until you identify where the units are located. Once you know where the units are placed within a converting factor, you can more easily determine what numbers go in the numerator and the denominator from an understanding of molar mass and coefficients. From an understanding of molar mass, the 2.016 accompanies the g H
2 and the 1.000 accompanies the mol H
2 in the first conversion factor. And from an understanding of the coefficients, the 3.000 accompanies the mol H
2 and the 2.000 accompanies the mol NH
3 in the second conversion factor. This is shown below.
Once you have layed out your conversion factors with units and numbers, you can determine the answer to the problem by taking the given amount (12.9 g H
2) and multiplying the 12.9 by all the numbers in the numerators of the conversion factors and dividing by all the numbers in the denominators of the conversion factors. The result is shown below.
As you gain comfort with the use of the factor-label method you will find that you are able to solve multi-step conversion problems by simply stringing together a collection of converting factors that cancel units in a step-wise fashion. In the next section we will see how three converstion factors can be strung together to convert from grams-to-moles-to-moles-to-grams.
Three Steps: Grams-to Grams Stoichiometry
A two-step stoichiometry problem involves converting from the grams of a substance to the moles of that substance (using a molar mass) to the moles of a second substance (using coefficients). (Two step problems can also include a mole-to-mole-to-gram conversion ... just the opposite as the aforementioned gram-to-mole-to-mole conversion.) Once you have mastered the two-step stoichiometry problems, it is time for a three-step problem. In a three-step problem, the mass of a reactant or product is given (in grams) and the problem demands that you determine the mass of another reactant or product.
As an example, suppose the reaction for ammonia sythesis is given
N2 + 3 H2 → 2 NH3
and the problem asks you to determine the mass of NH3 (in grams) produced from the reaction of 12.9 grams of H2. This is a three-step problem that starts like the two-step grams-to-moles-to-moles problem discussed above. First, use a molar mass value to convert from the given mass of H2 to the number of moles of H2. Second, use the coefficients to convert from the moles of H2 determined in the first step to the moles of NH3. And third, use the molar mass of NH3 to convert from the moles of NH3 determined in step 2 to the mass of NH3. The pathway is shown below.
The approach to this three-step problem using conversion factors will involve the use of three conversion factors. The unit cancellation step looks as follows:
And when numbers are inserted into the converting factors, the result looks like this:
Limiting and Excess Reactants
You will sometimes encounter a problem known as a limiting reactant problem or an excess reactant problem. Such problems can be quickly identified by looking to see if the problem statement reports the amount of two or more reactants. In such problems, there is no guarantee that the amount of reactant 1 or the amount of reactant 2 will be completely used up or reacted. To use a simple example, consider the synthesis of ammonia reaction once more:
N2 + 3 H2 → 2 NH3
The balanced equation calls for three times as many moles of hydrogen as nitrogen. But suppose that a problem states that 6.00 moles of H2 are combined with 1.00 moles of N2. In such a case, there is enough hydrogen to produce 4.00 moles of ammonia (NH3). Yet, there is not enough nitrogen to produce 4.00 moles of ammonia (NH3). There is only enough nitrogen to produce 2.00 moles of ammonia (NH3). So what happens? We say that the nitrogen limits the production of ammonia since the amount of NH3 that can be produced is limited by the amount of nitrogen that is present. The nitrogen is considered the limiting reactant in this situation. The amount of product produced will always be based on the amount of the limiting reactant that is available. And once all the N2 is used up (reacted away), there will be some left over hydrogen. Hydrogen is referred to as the excess reactant in this situation.
The limiting reactant can be identified as the reactant that produces the least amount of product. When the amounts of two or more reactants are provided, use each amount separatedly to determine the amount of product (in moles or in grams) each will produce if completely reacted. The reactant that produces the least amount is the limiting reactant. It is the reactant that limits the amount of product that can be formed. Base the calculation of the amount of product upon this reactant. The other reactant is the excess reactant. There will be some left over or excess of this reactant. To determine the amount of excess or left over reactant, do a stoichiometry calculation to determine how much of it reacts with the given amount of limiting reactant. Then subtract the reacted amount from the available or original amount in order to determine the left over amount.
There are two things to note in this discussion. First, N2 is not always the limiting reactant. And second, the limiting reactant is not necessarily the reactant that there is less of. To illustrate, let's suppose that the same ammonia synthesis reaction is considered but this time, there are 2.0 moles of N2 and 4.5 moles of H2 initially available. With these two given amounts, the H2 is the limiting reactant. The complete reaction of 2.00 moles of N2 will result in the 4.0 moles of NH3 produced. But the complete reaction of 4.5 moles of H2 results in only 3.0 moles of NH3 produced. Since hydrogen produces the least amount of product, it is the limiting reactant. The nitrogen is the excess reactant in this case. Since 1.5 moles of N2 will react with the 4.5 moles of the limiting reactant (H2), there will be 0.5 moles of N2 left over or in excess.
The discussion here was restricted to amounts in moles in order to keep the discussion simple. If amounts of reactants are given in grams, the principles remain the same. Stoichiometry will be used to determine which reactant amount produces the least amount of product so that the limiting reactant can be identified. The amount of product produced is based on this limiting reactant.