Mechanics: Simple Harmonic Motion
Simple Harmonic Motion: Problem Set Overview
There are six ready-to-use problem sets on the topic of Simple Harmonic Motion. Most problems are multi-part problems requiring an extensive analysis. The set of problems on this topic targets your ability to use the simple harmonic motion equations combined with force relationships to solve problems involving cyclical motion and springs.
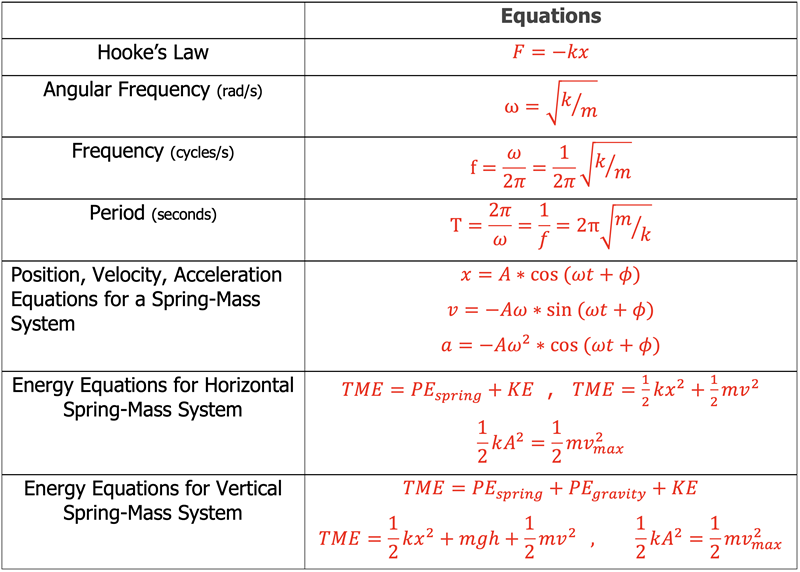
Hooke's Law
Consider the Spring-Mass system in a relaxed state as shown below. Notice that when the mass is pulled right or pushed left of the relaxed position the spring always tries to force the mass back to the relaxed position.
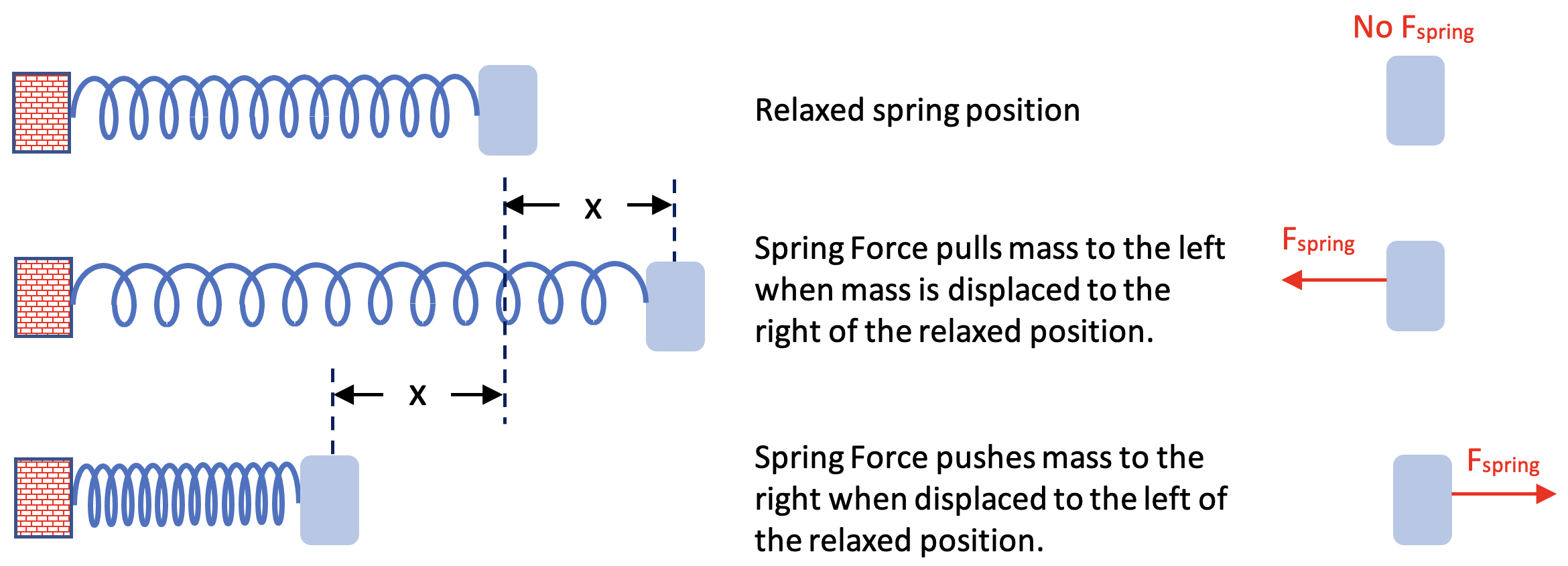
A spring is an object that exerts a force opposite the direction of displacement from its relaxed position. The spring force is also directly proportional to the amount of this displacement. Therefore, the spring force is defined as
Fspring = -k•x,
where k is the spring constant, x is the displacement from the relaxed position, and the negative sign indicates direction opposite the displacement from the relaxed position. This definition for spring force is known as Hooke’s Law.
Spring Potential Energy
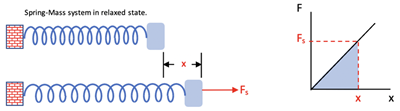 When the spring is pulled or pushed from its relaxed position work is done by an applied force. The amount of work done is stored Potential Energy in the spring. The situation at right shows a spring being pulled to the right a distance x. The force needed is shown in the graph; more force is required as the stretch of the spring increases. The area under the line is the work done by the force, Fs, to stretch the spring a distance, x. This can be calculated to be the area of the triangle, giving
When the spring is pulled or pushed from its relaxed position work is done by an applied force. The amount of work done is stored Potential Energy in the spring. The situation at right shows a spring being pulled to the right a distance x. The force needed is shown in the graph; more force is required as the stretch of the spring increases. The area under the line is the work done by the force, Fs, to stretch the spring a distance, x. This can be calculated to be the area of the triangle, giving
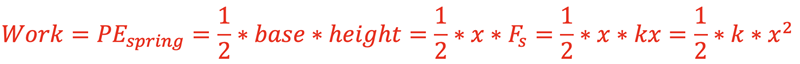
Simple Harmonic Motion
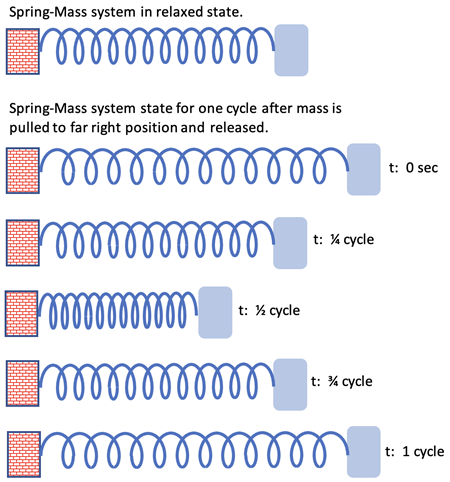 Consider an object of mass, m, on a frictionless, horizontal surface connected by a massless, relaxed spring to a fixed wall as shown at right. A force, F, is applied to pull the mass to a distance, x, from the relaxed position to the right. The mass is released at 0 seconds and begins speeding up from rest moving to the left, then slowing down, stopping, reversing direction, speeding up, and then slowing down back to the original starting position. The time to complete one cycle is called the period, T. This cycle repeats and will continue without interruption in the ideal case. This type of motion is called Simple Harmonic Motion; this is when the net force along the direction of motion follows Hooke’s Law.
Consider an object of mass, m, on a frictionless, horizontal surface connected by a massless, relaxed spring to a fixed wall as shown at right. A force, F, is applied to pull the mass to a distance, x, from the relaxed position to the right. The mass is released at 0 seconds and begins speeding up from rest moving to the left, then slowing down, stopping, reversing direction, speeding up, and then slowing down back to the original starting position. The time to complete one cycle is called the period, T. This cycle repeats and will continue without interruption in the ideal case. This type of motion is called Simple Harmonic Motion; this is when the net force along the direction of motion follows Hooke’s Law.
Relating Circular Motion to Simple Harmonic Motion
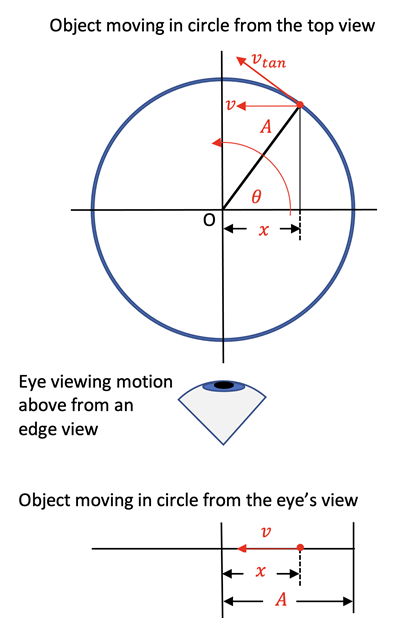 Looking at an object going around in a circle of radius, A, from the top view gives the relationships involving period, T in seconds/cycle, frequency, f in cycles/sec, and angular frequency, ω in rad/sec.
Looking at an object going around in a circle of radius, A, from the top view gives the relationships involving period, T in seconds/cycle, frequency, f in cycles/sec, and angular frequency, ω in rad/sec.
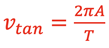
and rearranging gives
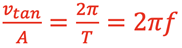
and
so
Looking at that same object going around in a circle of radius,
A, from the edge view reveals that the linear back and forth motion of the object is equivalent to the horizontal motion of an object on the end of a spring. Therefore, the radius,
A , is the same as the maximum amplitude of the mass-spring system and
vtan is the same as the maximum velocity of the mass as it passes through the position of the relaxed spring.
Simple Harmonic Motion Equations
Because the object moving in a circle follows a repeatable cyclic motion from the top view as shown previously the position of the mass in a spring-mass system in the edge on view as a function of time can be described by the equation
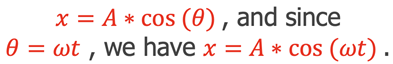
If the timing of the motion doesn’t start at the extreme position a phase angle is needed to establish the correct position values so that

where A, Amplitude, is the maximum displacement of the mass from the relaxed position,
ω, Omega, is the angular frequency, and
t, time, is a point in time after release from the initial position.
φ, phase angle, is the radian measure that gives the correct starting position at time t=0.
Calculus (not shown here) can be used to derive the equations for the velocity and acceleration of the mass in the spring-mass system from the position equation:
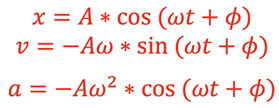
The
position,
velocity, and
acceleration versus
time values for a 100-gram object having an angular frequency of 3.14 rad/s, maximum amplitude of 10 cm, and a period of 2 seconds is shown in the graph below. The vertical axis is in cm for position, cm/s for velocity, and cm/s/s for acceleration while the horizontal axis is time in seconds.
The following values for
position,
velocity, and
acceleration can be determined from the previous equations at the times in the first column. The values can be verified by estimating from the graph.
The reference for position is 0 cm at the relaxed position of the spring, the middle position of the back-and-forth motion.
Simple Harmonic Motion Energy Considerations
Since there is no non-conservative force doing work on the mass as it cycles back and forth the Total Mechanical Energy of the mass is conserved:

where KE = ½•m•v2 is the kinetic energy of the motion, PE = ½•k•x2 is the potential energy in the spring. Let’s look at these values for the 0.5 second intervals of time as in the table above.
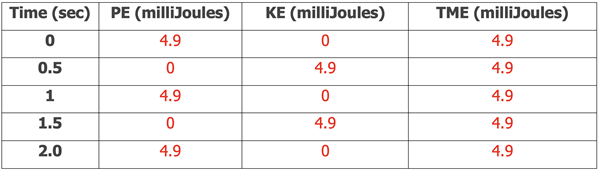
The energies would look like this in a graph. The vertical axis is in milliJoules for all energies while the horizontal axis is time in seconds.
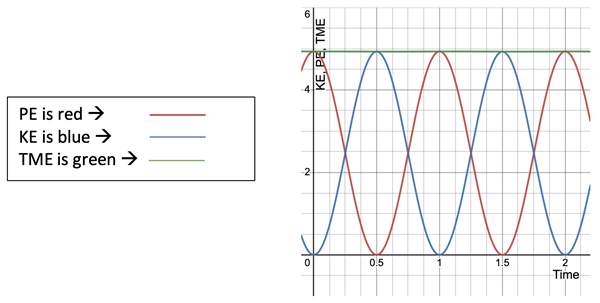
Relating Angular Frequency, Frequency, Period, Spring Constant, and Mass
We see from the energy analysis for the horizontal motion that the TME at the extreme positions is all Potential Energy of the spring and the TME at the middle position with the relaxed spring is all Kinetic Energy of the mass. Since TME is conserved these 2 maximum values of PE and KE must be equal.
Therefore,

Simple Harmonic Motion Equations for a Vertical Spring-Mass System
What happens in the vertical direction when the mass is pulled to a bottom position and released as shown below? Would it be true that the maximum Potential Energy due to the spring at the beginning of the cycle (t=0, v=0, h=0) is equal to the maximum Kinetic Energy at the equlibrium position (h=xmax) since the Potential Energy due to gravity is involved as well as the spring Potential Energy?
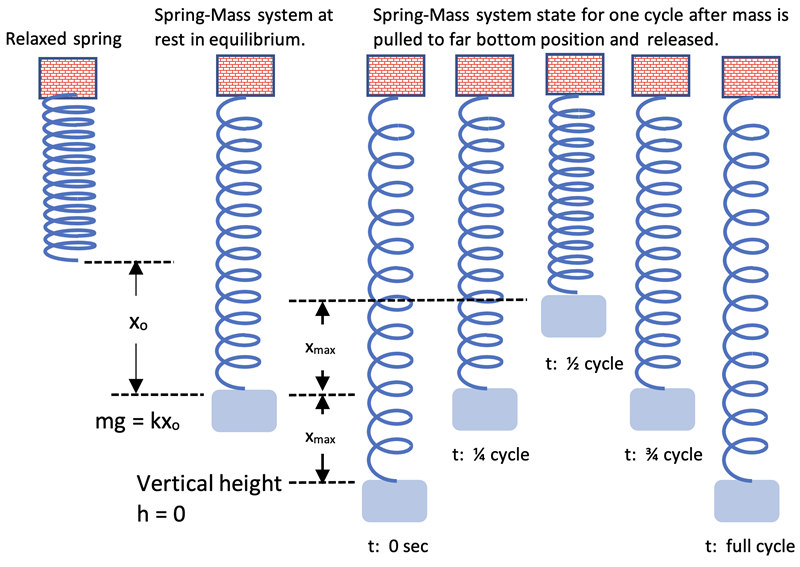
Let’s evaluate by starting with the relationship

at two positions of the mass (t=0 and t=¼cycle). Since no work is done by non-conservative forces then
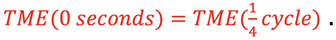
More specifically

Substituting the energy terms gives
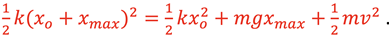
Expanding the left-hand side gives
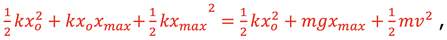
and since
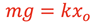
from the equilibrium position, then substituting on the right-hand side gives
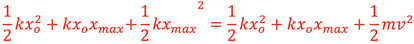
Canceling terms on each side gives
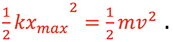
Therefore, the changing Potential Energy due to gravity can be neglected in this analysis to determine the maximum Kinetic Energy as it is accounted for by the Potential Energy stored in the spring using the true stretch of the spring, x, from the relaxed position. If the equilibrium vertical position is taken as the reference position of 0 and the mass is initially pulled below this position, the equations describing position, velocity, and acceleration will hold as they did in the horizontal SHM situation. This would make the downward direction positive. If the upward direction is desired to be positive a negative sign can be added to each equation to describe the motion as shown below.
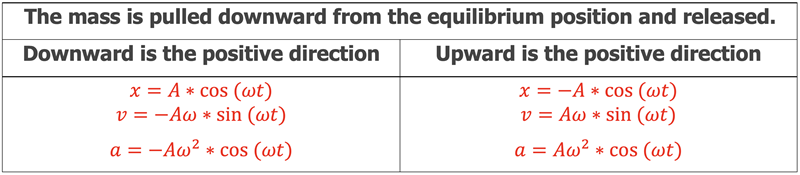
Simple Harmonic Motion Equations
We can now combine force, kinematic, and cyclic relationships to give the following:
Springs in Combination
Springs can be used in combination to produce a unique Spring-Mass behavior. All of the previous relationships can be used if an effective spring constant, k, is determined to analyze the system. Consider the series of identical springs hooked up to the same mass in the situations A – E below.
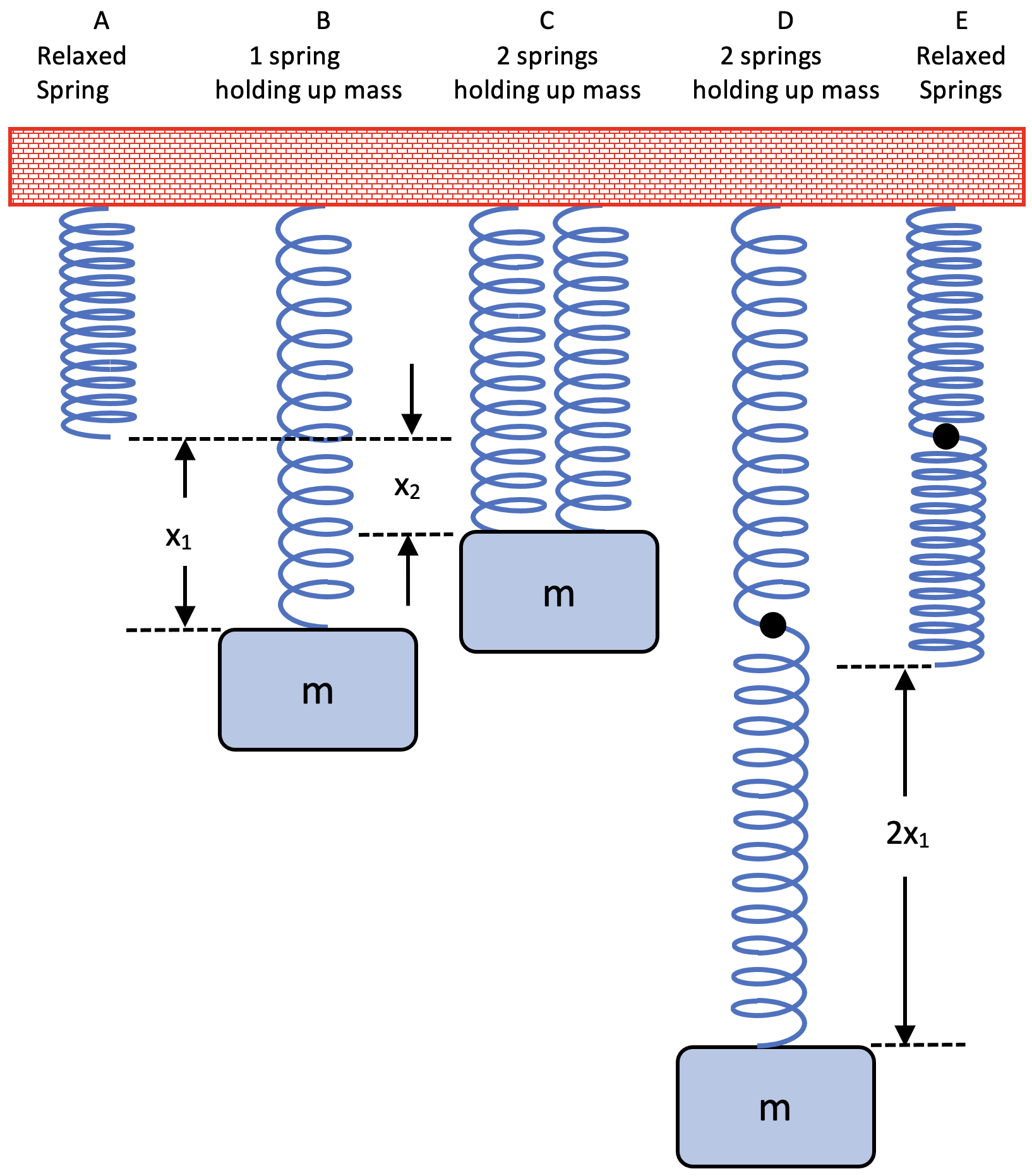
Consider analyzing the 2 springs in situation C acting in a parallel configuration. From equilibrium,
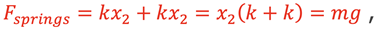
and considering the 2 springs as one effective spring,
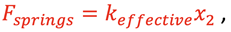
therefore,
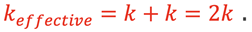
Consider analyzing the 2 springs in situation D acting in a series configuration. Each spring experiences the same force, mg, and stretches the same amount, x1. Then
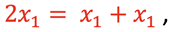
and from B,
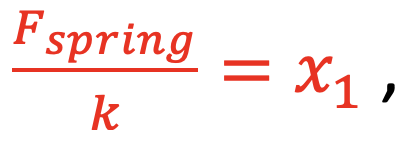
then
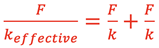
gives
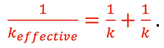
This can also be written as
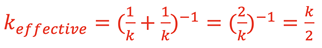
Spring Combination Results

Summary of Conditions for Simple Harmonic Motion
One difficulty a student may encounter with this topic is the confusion as to which formula to use. When approaching these problems it is suggested that you practice the usual habits of an effective problem-solver; identify known and unknown quantities in the form of the symbols of physics formulas, plot out a strategy for using the knowns to solve for the unknown, and then finally perform the necessary algebraic steps and substitutions required for the solution.
Habits of an Effective Problem-Solver
An effective problem solver by habit approaches a physics problem in a manner that reflects a collection of disciplined habits. While not every effective problem solver employs the same approach, they all have habits which they share in common. These habits are described briefly here. An effective problem-solver...
- ...reads the problem carefully and develops a mental picture of the physical situation. If needed, they sketch a simple diagram of the physical situation to help visualize it.
- ...identifies the known and unknown quantities in an organized manner, often times recording them on the diagram itself. They equate given values to the symbols used to represent the corresponding quantity (e.g., m = 1.50 kg, , k = 35.0 N/m, x = 0.15 m, vfinal = ???).
- ...plots a strategy for solving for the unknown quantity. The strategy will typically centers around the use of physics equations and is heavily dependent upon an understanding of physics principles.
- ...identifies the appropriate formula(s) to use, often times writing them down. Where needed, they perform the needed conversion of quantities into the proper unit.
- ...performs substitutions and algebraic manipulations in order to solve for the unknown quantity.
Read more...