Mechanics: Rotation and Torque
Rotation and Torque: Problem Set Overview
There are 14 ready-to-use problem sets on the topic of Rotation and Torque. The problems target your ability to use analyze a beam in terms of torque in order to determine the conditions for which it will and will not rotate.
Characteristics of Objects in Static Equilibrium
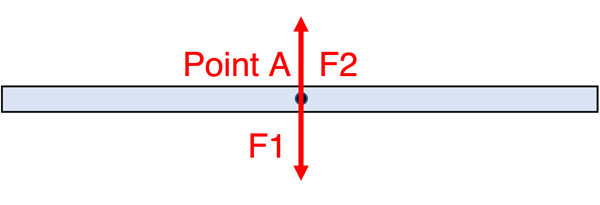
Objects in static equilibrium may experience forces in 2 perpendicular dimensions. Two of the three conditions that must be satisfied to make it a static situation are that ∑F = 0 N in both of those directions. For example, in the diagram below the magnitude of F1 is equal to the magnitude of F2 and the object can remain at rest since adding the 2 force vectors gives a zero net force.
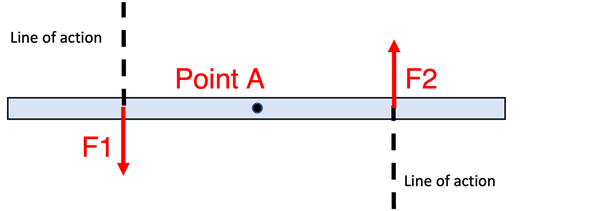
An issue that challenges static equilibrium arises when forces don’t share the same line of action (black dotted lines) as they did above. In the case below ∑F = 0 N is valid in the vertical direction, but since the position of F1 and F2 are offset from each other the object would rotate around Point A in a counterclockwise direction. We say that these forces individually will cause a torque, and since both try to rotate the object counterclockwise, they will produce a net torque resulting in rotation, about point A.
Mathematical Analysis of Objects Experiencing Torques
In order to analyze the torque on an object mathematically we use the definition of the torque vector cross product equation: τ = r x F where the symbol τ (Greek letter tau, pronunciation) represents Torque. This mathematical analysis of torque is heavily dependent upon an understanding of the vector cross product between r (position vector from Point A to the position of force applied) and F (force vector on the object) in the definition. The operation of the mathematical cross product creates a third vector perpendicular to the original 2 vectors using the right-hand rule as shown below. The index finger points in the direction of r, the middle finger curls into the direction of F, and the thumb points in the direction of τ. If r and F are in the x-y plane the torque vector, τ would be in the z axis direction.
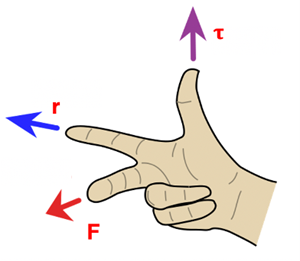
Image Credit: https://commons.wikimedia.org/wiki/File:Right_hand_rule_cross_product.svg
To see how to calculate a value of the torque vector let’s consider the single force, F, on the generic object below with a pin joint present at point A (this will be the axis of rotation on a line in and out of the page). Since the force, F, does not lie on a line of action passing through point A it will rotate the object about that point.
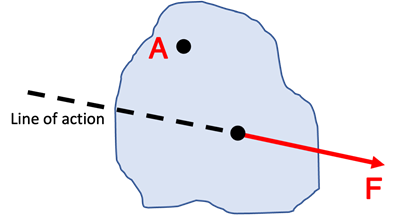
The position vector, r, connects the axis of rotation (Point A) to the point at which the force is applied to the object as shown below.
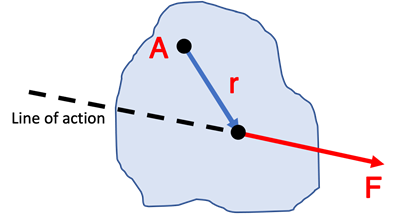
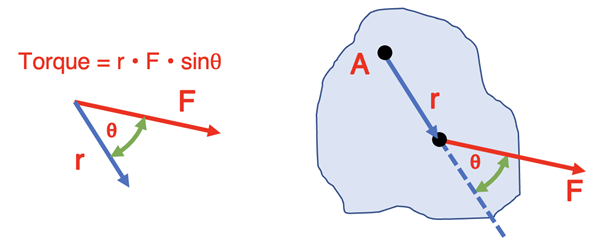
The evaluation of the vector cross product using r and F in an algebraic calculation is shown below left. The relationship of r, F, and θ relative to point A is shown below right.
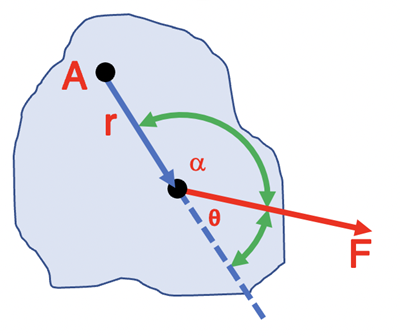
An equivalent evaluation of the cross product would be to use the angle, α, as shown below. This angle is supplementary to θ so the value of r•F•sinα will produce the same value as the previous method since the 2 angles will produce the same sine value.
Other ways to Complete the Vector Cross Product Calculation
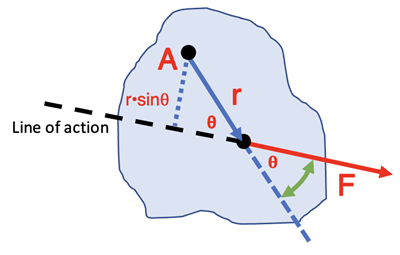
There are other ways to evaluate the cross product. One is to use a perpendicular distance from the axis point (Point A) to the line of action of the force as shown below (blue dotted line). This perpendicular distance is sometimes called the “lever arm” or “moment arm”. The torque value will then be “lever arm * Force” and evaluate to be r•sinθ•F. This would produce the same value as the previous method.
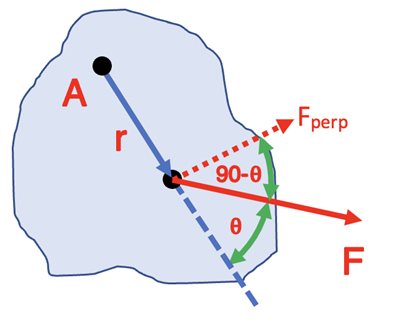
Another way would be to use the component of F perpendicular to the position vector, r, as shown below. The torque would be evaluated as “r * Fperp” which is equal to r•F•cos(90-θ) that once again would produce the same value as r•F•sinθ.
Net Torque and Direction
The goal of the Torque analysis is to determine the magnitude of all torque values from individual forces that are on lines of action not passing through the chosen axis of rotation point. These will then determine the overall torque (Net Torque or ∑τ) upon the object.
We can more easily conceptualize this analysis by determining whether the force vectors are trying to rotate the object clockwise or counterclockwise in the plane of the position vector, r, and force vector, F, about the point chosen. We would then proceed by adding all the torque values in the counterclockwise direction and subtracting all torques in the clockwise direction. If this sum is equal to 0 then the third condition for static equilibrium is satisfied: ∑τ = 0.
Summary of Conditions for Static Equilibrium
One difficulty a student may encounter with this topic is the confusion as to which formula to use. The table below provides a useful summary of the formulae pertaining to torque and rotary motion. When approaching these problems it is suggested that you practice the usual habits of an effective problem-solver; identify known and unknown quantities in the form of the symbols of physics formulas, plot out a strategy for using the knowns to solve for the unknown, and then finally perform the necessary algebraic steps and substitutions required for the solution.
x direction:
∑Fx = 0
y direction:
∑Fy = 0
Any point chosen:
∑τ = 0
Habits of an Effective Problem-Solver
An effective problem solver by habit approaches a physics problem in a manner that reflects a collection of disciplined habits. While not every effective problem solver employs the same approach, they all have habits which they share in common. These habits are described briefly here. An effective problem-solver...
- ...reads the problem carefully and develops a mental picture of the physical situation. If needed, they sketch a simple diagram of the physical situation to help visualize it.
- ...identifies the known and unknown quantities in an organized manner, often times recording them on the diagram itself. They equate given values to the symbols used to represent the corresponding quantity (e.g., m = 1.50 kg, , F = 12.2 N, r = 0.133 m, Torque = ???).
- ...plots a strategy for solving for the unknown quantity. The strategy will typically center saround the use of physics equations and is heavily dependent upon an understanding of physics principles.
- ...identifies the appropriate formula(s) to use, often times writing them down. Where needed, they perform the needed conversion of quantities into the proper unit.
- ...performs substitutions and algebraic manipulations in order to solve for the unknown quantity.
Read more...