 Standing Wave Maker
Standing Wave Maker
Resource:
Physics Interactives: Standing Wave Patterns
Grade Level: High School
Description:
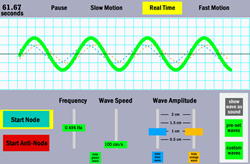
This simulation provides a robust set of tools for investigating the behavior and mathematics of standing waves. Learners can choose the parameter of two fixed ends, one open end, or two open ends and watch the wave formation in real time, slow motion, or fast motion. Pre-set options allow quick cycling through various harmonics for both waves on a string and standing waves in air columns. Appropriate for students with prior knowledge of basic wave properties.
This activity aligns with the three dimensions of the Next Generation Science Standards in the manner described below:
| Wave Properties (HS-PS4.A.3): Waves can add or cancel one another as they cross, depending on their relative phase (i.e., relative position of peaks and troughs of the waves), but they emerge unaffected by each other. |
This simulation illustrates how standing waves are formed by the interference of two waves moving in the opposite direction through the same medium. Students can choose to view a wave on a string or a sound wave. Press + or – to cycle through various harmonics, and the simulation automatically generates values of changing period and frequency. It provides the computational basis for students to see the relationship of frequency, period, and wavelength in a standing wave pattern. Advanced students can apply their knowledge to create custom wave patterns. |
| Patterns: Mathematical representations are needed to identify some patterns. |
The simulation is designed to give explicit support in understanding the patterns that occur in standing waves, a type of interference phenomenon. Watching a demonstration or video of standing waves is often not sufficient to foster understanding of why standing waves occur or how their patterns can be predicted. The Standing Wave Maker lets students build their own standing wave patterns and explore the mathematical relationships that emerge. By clicking + or – on the screen, the learner can move from one harmonic to the next, up to the 12th harmonic. At each interval, the model displays changing values of frequency, period, and wavelength. Students can use these values to figure out the mathematical relationships. |
| Structure and Function: The functions and properties of natural objects and systems can be inferred from their overall structure, the way their components are shaped and used, and the molecular substructures of their various materials. |
This model is intended to help students understand the unique circumstances that must occur for a waveform to achieve the appearance of “standing still”. By choosing the “View as Sound” option, learners can readily investigate how the structures of open-and-closed-end air columns affect the shape of a sound wave. By cycling through the 12 harmonics in the simulation, it will be easier to visualize the structure of nodes and antinodes that characterize a standing wave pattern. |
| Developing and Using Models – Develop or use a model based on evidence to illustrate the relationships between components of a system. |
The Standing Wave Maker allows students to create their own standing wave patterns or follow pre-set options. With either choice, learners can use the model to explore what happens if the medium has two fixed ends, one open end, or two open ends. Students can also move from 1st through 12th harmonic and back again to see the predictable changes in shapes of nodes and antinodes in the wave pattern. Modeling these patterns provides a concrete experience for learners to investigate standing waves in ways that would be impossible through textbooks or still images. |
| Using Mathematics and Computational Thinking – Create a computational model or simulation of a phenomenon, designed device, process, or system. |
The Standing Wave Maker lets students explore mathematical relationships that emerge in a standing wave pattern. By clicking + or – on the screen, the learner can move from one harmonic to the next, up to the 12th harmonic. At each interval, the model displays changing values of frequency, period, and wavelength. Students can use these values to calculate the mathematical relationships among these variables. |
Associated Reading from The Physics Classroom
Other Supporting Pages at The Physics Classroom:
View Infographic.
(Coming Soon)
Search the NGSS Corner
Maybe you're looking for something really specific that pertains to a desired topic and emphasizes one or more of the listed NGSS dimensions. Why not try a search of this section of our website? Simply select from one or more of the pull-down menus and click Search This page will reload and a collection of possibilities will be displayed in this section of the page and sorted by relevancy.