A standing wave pattern is a vibrational pattern created within a medium when the vibrational frequency of the source causes reflected waves from one end of the medium to interfere with incident waves from the source. This interference occurs in such a manner that specific points along the medium appear to be standing still. Because the observed wave pattern is characterized by points that appear to be standing still, the pattern is often called a standing wave pattern. Such patterns are only created within the medium at specific frequencies of vibration. These frequencies are known as harmonic frequencies, or merely harmonics. At any frequency other than a harmonic frequency, the interference of reflected and incident waves leads to a resulting disturbance of the medium that is irregular and non-repeating.
How is a Standing Wave Formed?
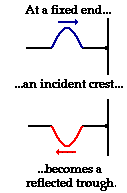
But how are standing wave formations formed? And why are they only formed when the medium is vibrated at specific frequencies? And what makes these so-called harmonic frequencies so special and magical? To answer these questions, let's consider a snakey stretched across the room, approximately 4-meters from end to end. (A "snakey" is a slinky-like device that consists of a large concentration of small-diameter metal coils.) If an upward displaced pulse is introduced at the left end of the snakey, it will travel rightward across the snakey until it reaches the fixed end on the right side of the snakey. Upon reaching the fixed end, the single pulse will reflect and undergo inversion. That is, the upward displaced pulse will become a downward displaced pulse. Now suppose that a second upward displaced pulse is introduced into the snakey at the precise moment that the first crest undergoes its fixed end reflection. If this is done with perfect timing, a rightward moving, upward displaced pulse will meet up with a leftward moving, downward displaced pulse in the exact middle of the snakey. As the two pulses pass through each other, they will undergo destructive interference. Thus, a point of no displacement in the exact middle of the snakey will be produced. The animation below shows several snapshots of the meeting of the two pulses at various stages in their interference. The individual pulses are drawn in blue and red; the resulting shape of the medium (as found by the principle of superposition) is shown in green. Note that there is a point on the diagram in the exact middle of the medium that never experiences any displacement from the equilibrium position.
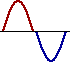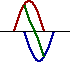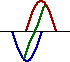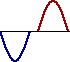
An upward displaced pulse introduced at one end will destructively interfere in the exact middle of the snakey with a second upward displaced pulse introduced from the same end if the introduction of the second pulse is performed with perfect timing. The same rationale could be applied to two downward displaced pulses introduced from the same end. If the second pulse is introduced at precisely the moment that the first pulse is reflecting from the fixed end, then destructive interference will occur in the exact middle of the snakey.
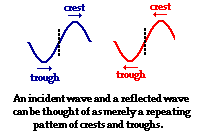The above discussion only explains why two pulses might interfere destructively to produce a point of no displacement in the middle of the snakey. A wave is certainly different than a pulse. What if there are two waves traveling in the medium? Understanding why two waves introduced into a medium with perfect timing might produce a point of displacement in the middle of the medium is a mere extension of the above discussion. While a pulse is a single disturbance that moves through a medium, a wave is a repeating pattern of crests and troughs. Thus, a wave can be thought of as an upward displaced pulse (crest) followed by a downward displaced pulse (trough) followed by an upward displaced pulse (crest) followed by a downward displaced pulse (trough) followed by... . Since the introduction of a crest is followed by the introduction of a trough, every crest and trough will destructively interfere in such a way that the middle of the medium is a point of no displacement.
The Importance of Timing
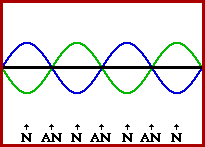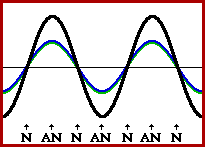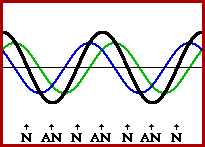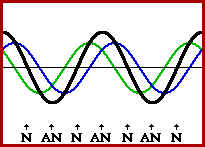
Of course, this all demands that the timing is perfect. In the above discussion, perfect timing was achieved if every wave crest was introduced into the snakey at the precise time that the previous wave crest began its reflection at the fixed end. In this situation, there will be one complete wavelength within the snakey moving to the right at every instant in time; this incident wave will meet up with one complete wavelength moving to the left at every instant in time. Under these conditions, destructive interference always occurs in the middle of the snakey. Either a full crest meets a full trough or a half-crest meets a half-trough or a quarter-crest meets a quarter-trough at this point. The animation below represents several snapshots of two waves traveling in opposite directions along the same medium. The waves are interfering in such a manner that there are points of no displacement produced at the same positions along the medium. These points along the medium are known as nodes and are labeled with an N. There are also points along the medium that vibrate back and forth between points of large positive displacement and points of large negative displacement. These points are known as antinodes and are labeled with an AN. The two individual waves are drawn in blue and green and the resulting shape of the medium is drawn in black.
There are other ways to achieve this perfect timing. The main idea behind the timing is to introduce a crest at the instant that another crest is either at the halfway point across the medium or at the end of the medium. Regardless of the number of crests and troughs that are in between, if a crest is introduced at the instant another crest is undergoing its fixed end reflection, a node (point of no displacement) will be formed in the middle of the medium. The number of other nodes that will be present along the medium is dependent upon the number of crests that were present in between the two timed crests. If a crest is introduced at the instant another crest is at the halfway point across the medium, then an antinode (point of maximum displacement) will be formed in the middle of the medium by means of constructive interference. In such an instance, there might also be nodes and antinodes located elsewhere along the medium.
A standing wave pattern is an interference phenomenon. It is formed as the result of the perfectly timed interference of two waves passing through the same medium. A standing wave pattern is not actually a wave; rather it is the pattern resulting from the presence of two waves (sometimes more) of the same frequency with different directions of travel within the same medium. The physics of musical instruments has a basis in the conceptual and mathematical aspects of standing waves. For this reason, the topic will be revisited in the Sound and Music unit at The Physics Classroom Tutorial.
We Would Like to Suggest ...
Why just read about it and when you could be interacting with it? Interact - that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Standing Wave Patterns Interactive. You can find it in the Physics Interactives section of our website. The
Standing Wave Patterns Interactive provides the learner an environment for exploring the formation of standing waves, standing wave patterns, and mathematical relationships for standing wave patterns.