Mechanics: 1-Dimensional Kinematics
Calculator Pad, Version 2
You are viewing the Legacy Version of The Calculator Pad. We have recently revised and improved The Calculator Pad.
Version 2 is now LIVE! We have more than tripled the number of problems, broken each unit into several smaller, single-topic problem sets, and utilized a random number generator to provide numerical information for each problem. Student answers are automatically evaluated and feedback is instant. And we've maintained the same commitment to providing help via links to existing resources. While the FREE version does all the above, teachers with a Task Tracker subscription can take things a step further. They can modify our pre-made problem sets, write their own problems with our easy-to-use Problem Builder, and use the Calculator Pad to design their own program that expresses their emphasis on the use of mathematics in Physics.
Return to the
Main Page to link into Version 2. Learn more
About Version 2. Or visit the
Store to make a Task Tracker purchase.
1-D Kinematics Problem Set
Problem 1
In the 2008 Olympics, Jamaican sprinter Usain Bolt shocked the world as he ran the 100-meter dash in 9.69 seconds. Determine Usain's average speed for the race.
Problem 2
In the Funny Car competition at the Joliet Speedway in Joliet, Illinois in October of 2004, John Force complete the ¼-mile dragster race in a record time of 4.437 seconds. Determine the average speed of the dragster in mi/hr and m/s. GIVEN: (1.000 mi =1609 m)
Problem 3
In the qualifying round of the 50-yd freestyle in the sectional swimming championship, Dugan got an early lead by finishing the first 25.00 yd in 10.01 seconds. Dugan finished the return leg (25.00 yd distance) in 10.22 seconds.
a. Determine Dugan's average speed for the entire race.
b. Determine Dugan's average speed for the first 25.00 yd leg of the race.
c. Determine Dugan's average velocity for the entire race.
Problem 4
In last week's Homecoming victory, Al Konfurance, the star halfback of South's football team, broke a tackle at the line of scrimmage and darted upfield untouched. He averaged 9.8 m/s for an 80-yard (73 m) score. Determine the time for Al to run from the line of scrimmage to the end zone.
Problem 5
During the annual shuffleboard competition, Renee gives her puck an initial speed of 9.32 m/s. Once leaving her stick, the puck slows down at a rate of -4.06 m/s/s.
a. Determine the time it takes the puck to slow to a stop.
b. Use your initial speed and the calculated time to determine the average speed and the distance which the puck travels before stopping.
Problem 6
Ken Runfast is the star of the cross-country team. During a recent morning run, Ken averaged a speed of 5.8 m/s for 12.9 minutes. Ken then averaged a speed of 6.10 m/s for 7.1 minutes. Determine the total distance which Ken ran during his 20 minute jog.
Problem 7
The Lamborghini Murcielago can accelerate from 0 to 27.8 m/s (100 km/hr or 62.2 mi/hr) in a time of 3.40 seconds. Determine the acceleration of this car in both m/s/s and mi/hr/s.
Problem 8
Homer Agin leads the Varsity team in home runs. In a recent game, Homer hit a 96 mi/hr sinking curve ball head on, sending it off his bat in the exact opposite direction at 56 mi/hr. The actually contact between ball and bat lasted for 0.75 milliseconds. Determine the magnitude of the average acceleration of the ball during the contact with the bat. Express your answer in both mi/hr/s and in m/s/s. (Given: 1.00 m/s = 2.24 mi/hr)
Problem 9
A Formula One car is a single-seat racing car with an open cockpit and substantial wings located in the front and rear. At high speeds, the aerodynamics of the car help to create a strong downward force which allows the car to brake from 27.8 m/s (100 km/hr or 62.2 mi/hr) to 0 in as small of a distance as 17 meters. Determine the deceleration rate (i.e., acceleration) achieved by such a car.
Problem 10
The position-time graph below represents the motion of South's basketball coach during the last sixteen seconds of overtime during this past weekend's game.
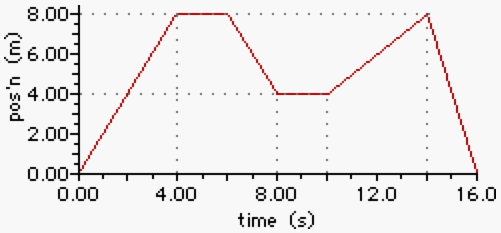
Use the graph to answer the next several questions.
a. Determine the total distance walked by the coach during these 16 seconds.
b. Determine the resulting displacement of the coach during these 16 seconds.
c. Determine the displacement of the coach after 12.0 seconds.
d. At what time did the coach have the greatest displacement from his starting position?
e. What was the fastest speed which the coach walked during any of the time intervals for the last 16.0 seconds?
f. What was the average speed of the coach for these 16.0 seconds?
Problem 11
Mr. H is preparing to show the class a Strobe demonstration when he realizes that his absent-mindedness has struck once more. He left the strobe on the counter in the back of the lab after the last class period. Starting 1.0 meter from the front of the room, Mr. H walks quickly to the back of the lab, picks up the strobe and returns to the middle of the classroom. The position-time graph below represents his motion. Use the graph to answer the next several questions.
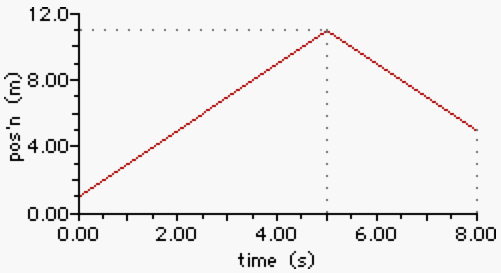
a. What is the total distance walked by Mr. H during these 8.0 seconds?
b. What is the average speed of Mr. H during these 8.0 seconds?
c. What is the average velocity of Mr. H during these 8.0 seconds?
d. How fast did Mr. H walk during the first 5.0 seconds?
e. How fast did Mr. H walk during the last 3.0 seconds?
Problem 12
The position-time graph below represents the motion of two students - Mac (in red) and Tosh (in blue) - as they enter and exit the school library during a passing period.
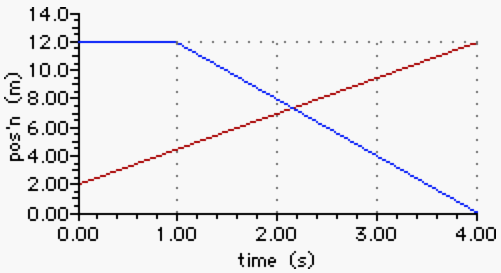
Use the graph to determine the speeds at which the two students move. (Ignore any stationary periods of time.) Then determine how much faster the fastest student moves than the slower student.
Problem 13
Renatta Gas did it again. She failed to fill up her tank during the last four weeks. The velocity-time graph below represents the last six seconds of motion her car before being stranded on a highway in route to her university.
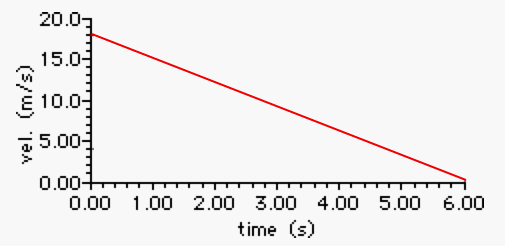
Use this graph to determine...
a. ...the acceleration of Renatta's car.
b. ...the distance traveled during her last 6.0 seconds of motion.
Problem 14
Marcus Tardee is driving his friends to school. With the start of school being only minutes away, he is unfortunately following a slow garbage truck. The truck finally turns down a side street and Marcus accelerates to a much more customary speed. The velocity-time graph below represents his motion. Use the graph to answer the following questions.
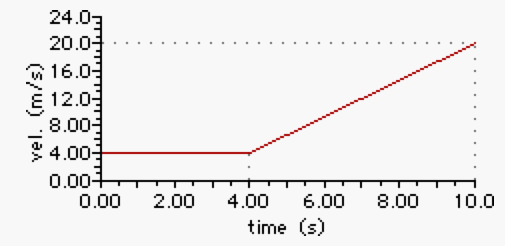
a. How fast was Marcus traveling while following the garbage truck?
b. Determine the distance traveled during the first 4.0 seconds represented on the graph.
c. Determine the acceleration of the car once the garbage truck turned onto the side street.
d. Determine the distance traveled by the car during the last 6.0 seconds of motion.
Problem 15
The velocity-time graph below represents the motion of a car on a city street.
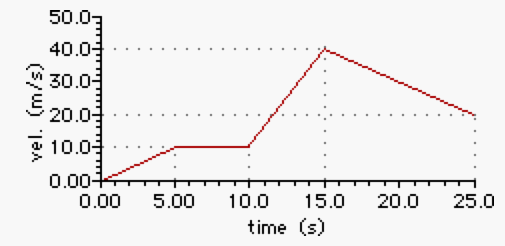
Use the graph to determine the acceleration values of the car at ...
a. 1.4 seconds.
b. 6.8 seconds.
c. 11.6 seconds.
d. 17.6 seconds.
Problem 16
After a long soccer practice down at the neighborhood soccer fields, Suzie begins walking up the steep hill towards her home. She gives her soccer ball a kick up the hill and continues walking towards it, meeting the ball as it is rolling back down. The velocity-time graph below depicts the motion of the ball. Use the graph to answer the following questions.
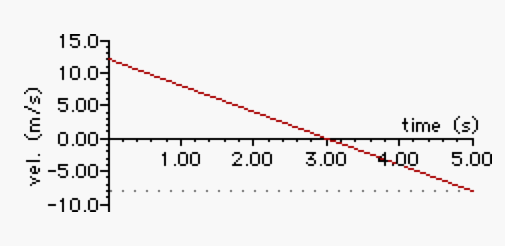
a. At what time did the ball change directions and begin rolling back down the hill?
b. What is the acceleration of the ball as it rolls up the hill? down the hill?
c. How far up the hill did the ball roll before it began to roll back down?
d. Determine the total distance traveled by the ball during the 5.00 seconds - both the distance up the hill and down the hill.
e. How far up the hill did Suzie walk between the time when she kicked the ball and the time she met up with the ball (at 5.0 seconds)?
Problem 17
Jeremy has recently taken up snowboarding as a hobby. He is practicing making smooth turns while traveling up sloped inclines. The velocity-time graph below depicts his motion traveling up an embankment and part-way down. Use the graph to answer the following questions.
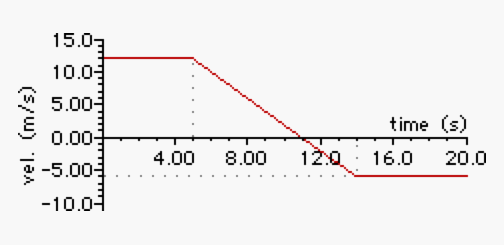
a. Determine Jeremy's acceleration at 8.0 seconds.
b. Determine the distance Jeremy traveled from 0.0 to 5.0 seconds.
c. At what time did Jeremy begin to travel back down the embankment?
Problem 18
A Cessna 150 airplane has a takeoff speed of 28 m/s (63 mi/hr). Determine the minimum length of the runway which would be required for the plane to take off if it averages an acceleration of 1.9 m/s/s.
Problem 19
Cynthia competes in luge competitions during the winter months. She rides solo on a small sled 3 inches off the ground down icy slopes, turning only by use of her feet and the shifting of her weight on the sled. During the initial stage of one downhill luge, Cynthia accelerated from rest at 6.84 m/s/s for 2.39 seconds. Determine the distance she moved during this acceleration phase.
Problem 20
Suzie Lavtaski has reached the end of the ski slope and abruptly decelerates from 29.0 m/s to 1.8 m/s in 1.45 seconds. Determine Suzie' acceleration rate and the distance she moved during this braking period.
Problem 21
Captain John Stapp is often referred to as the "fastest man on Earth." In the late 1940s and early 1950s, Stapp ran the U.S. Air Force's Aero Med lab, pioneering research into the accelerations which humans could tolerate and the types of physiological effects which would result. After several runs with a 185-pound dummy named Oscar Eightball, Captain Stapp decided that tests should be conducted upon humans. Demonstrating his valor and commitment to the cause, Stapp volunteered to be the main subject of subsequent testing.
Manning the rocket sled on the famed Gee Whiz track, Stapp tested acceleration and deceleration rates in both the forward-sitting and backward-sitting positions. He would accelerate to aircraft speeds along the 1200-foot track and abruptly decelerate under the influence of a hydraulic braking system. On one of his most intense runs, his sled decelerated from 282 m/s (632 mi/hr) to a stop at -201 m/s/s. Determine the stopping distance and the stopping time.
Problem 22
Julietta and Jackson are playing miniature golf. Julietta's ball rolls into a long. straight upward incline with a speed of 2.95 m/s and accelerates at -0.876 m/s/s for 1.54 seconds until it reaches the top of the incline and then continues along an elevated section. Determine the length of the incline.
Problem 23
Rickey Henderson, baseball's record holder for stolen bases, approaches third base. He dives head first, hitting the ground at 6.75 m/s and reaching the base at 5.91 m/s, accelerating at -5.11 m/s/s. Determine the distance Rickey slides across the ground before touching the base.
Problem 24
Win Blonehare and Kent Swimtashore are sailboating in Lake Gustastorm. Starting from rest near the shore, they accelerate with a uniform acceleration of 0.29 m/s/s, How far are they from the shore after 18 seconds?
Problem 25
For years, the tallest tower in the United States was the Phoenix Shot Tower in Baltimore, Maryland. The shot tower was used from 1828 to1892 to make lead shot for pistols and rifles and molded shot for cannons and other instruments of warfare. Molten lead was dropped from the top of the 234-foot (71.3 meter) tall tower into a vat of water. During its free fall, the lead would form a perfectly spherical droplet and solidify. Determine the time of fall and the speed of a lead shot upon hitting the water at the bottom.
Problem 26
According to Guinness, the tallest man to have ever lived was Robert Pershing Wadlow of Alton, Illinois. He was last measured in 1940 to be 2.72 meters tall (8 feet, 11 inches). Determine the speed which a quarter would have reached before contact with the ground if dropped from rest from the top of his head.
Problem 27
A California Condor is approaching its nest with a large chunk of carrion in its beak. As it approaches, it makes an upward swoop, achieving a momentary upward velocity of 12.8 m/s when the carrion falls from its mouth, hitting a cliff outcropping 32.1 m below. Determine the speed of the carrion upon hitting the outcropping.
Problem 28
During his recent skydiving adventure, Luke Autbeloe had reached a terminal speed of 10.4 m/s as he approached the ground with his parachute. During an attempt to snap one last photo with his camera, Luke fumbled it from a height of 52.1 m above the ground.
a. Determine the speed with which the camera hits the ground.
b. Determine the time for the camera to free fall from Luke's hands to the ground.
Problem 29
The speed required of a military jet when taking off from the deck of an aircraft carrier is dependent upon the speed of the carrier and the speed of the wind into which the carrier is moving. The takeoff speed required of a military jet relative to the deck of the carrier is 45 m/s when the carrier travels at 45 mi/hr into a 20 mi/hr wind. And when the aircraft carrier is traveling at 10 mi/hr into a 5 mi/hr wind, the takeoff speed relative to the deck of the carrier is 71 m/s. Determine the acceleration which a military jet must have to take off under these two conditions from the 126-m long runway of the USS Ronald Reagan aircraft carrier.
Problem 30
The Zero Gravity Research Facility at NASA-operated Glenn Research Center in Ohio is used to test the behavior of fluids, flames, equipment and other objects in free fall. It consists of a 467-foot long, 12-foot diameter, steel vacuum chamber. The steel chamber resides inside of a concrete lined shaft which extends 510 feet below ground level. Objects falling through the tower experience free fall over a distance of 432 feet (132 meters).
a. Determine the falling time for objects dropped from rest.
b. Determine the final speed of the objects before the braking period begins.
Problem 31
It's breakfast time and Mr. H entertains himself once more by watching the daily beetle race across the 35.7-cm length of the Wheaties box top. Angie the beetle typically averages 3.77 mm/s and Bessie the beetle averages 4.78 mm/s. If Bessie gives Angie a 5.4 cm head start, then which beetle wins and by what distance?
Problem 32
Alexander's hobby is dirt biking. On one occasion last weekend, he accelerated from rest to 17.8 m/s/s in 1.56 seconds. He then maintained this speed for 9.47 seconds. Seeing a coyote cross the trail ahead of him, he abruptly stops in 2.79 seconds. Determine Alexander's average speed for this motion.
Problem 33
Ima Rushin can travel from Milwaukee Avenue to the school entrance gate at a constant speed of 22.5 m/s when the lights are green and there is no traffic. On Wednesday, Ima is stopped by a red light at Landwehr Road. She decelerates at -3.95 m/s/s, waits for 45.0 seconds before the light turns green and accelerates back up to speed at 4.91 m/s/s.
a. Determine the total time required to decelerate, stop and accelerate back up to speed.
b. Determine the amount of time the red light costs the driver (compared to if the car had not been stopped by the red light).
Problem 34
A tortoise and a hare are having a 1000-meter race. The tortoise runs the race at a constant speed of 2.30 cm/s. The hare moves at an average speed of 1.50 m/s for 10.0 minutes and then decides to take a nap. After waking up from the nap, the hare recognizes that the tortoise is about to cross the finish line and immediately accelerates from rest with a constant acceleration of 0.500 m/s/s for the remaining distance of the race. If the tortoise wins by a hair (no pun intended), then what is the time in hours that the hare napped?
Problem 35
Hayden and Matthew are riding around the neighborhood on their scooters. Hayden is at rest when Matthew passes him moving at a constant speed of 0.37 m/s. After 1.8 seconds, Hayden decides to chase after Matthew, accelerating at 0.91 m/s/s. How much time must Hayden accelerate before he is side-by-side with Matthew?
Return to
Overview
View Audio Guided Solution for Problem:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35